
Question Number 3003 by Rasheed Soomro last updated on 02/Dec/15

$${What}\:{is}\:{nth}\:{term}? \\ $$$$\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{5}}{\mathrm{4}},\frac{\mathrm{15}}{\mathrm{8}},\frac{\mathrm{37}}{\mathrm{16}},\frac{\mathrm{83}}{\mathrm{32}}... \\ $$
Commented by Rasheed Soomro last updated on 05/Dec/15

$$\underset{−} {\mathcal{HIGH}{ly}}\:\mathcal{A}{ppriciate}\:\mathcal{Y}{our}\:\overset{\mathcal{VALUEABLE}} {\mathcal{G}{uidance}}! \\ $$
Commented by prakash jain last updated on 04/Dec/15
![a_1 =1 a_2 =5 a_3 =15 a_4 =37 a_5 =83 b_n =a_n −a_(n+1) b_1 =−4 b_2 =−10 b_3 =−22 b_4 =−46 c_1 =6 c_2 =12 c_3 =24 c_n =b_n −b_(n+1) d_1 =−6 d_2 =−12 d_n =c_n −c_(n+1) d_n =−6n c_(n+1) =c_n −d_n =c_n +6n (c_1 =6) c_2 =6+6×1 c_3 =6+6×1+6×2 c_n =6+3(n−1)n b_(n+1) =b_n −c_n =b_n −6−3(n−1)n, b_1 =−4 b_2 =−4−6−3(0)(1)=−10 b_3 =−4−6−3(0)(1)−6−3(1)(2)=−22 b_4 =−4−6−3(0)(1)−6−3(1)(2)−6−3(2)(3)=−46 b_n =−4−6(n−1)−3Σ_(i=1) ^(n−1) (i−1)(i) a_(n+1) =a_n −b_n a_2 =a_1 −b_1 =1+4+6(0)+3Σ_(i=1) ^0 (i−1)(i)=5 a_3 =1+4+6(0)+3Σ_(i=1) ^0 (i−1)(i)+4+6(1)+3Σ_(i=1) ^1 (i−1)(i) =1+4+0+0+4+6+3(0) a_n =1+4(n−1)+3(n−2)(n−1)+3Σ_(j=1) ^(n−2) Σ_(i=1) ^j (i−1)i applying above formula a_1 =1 a_2 =1+4+0+0=5 a_3 =1+4×2+3(1)(2)+3[Σ_(i=1) ^1 (i−1)i] =1+8+6+3[0]=15 a_4 =1+4×3+3(2)(3)+3[Σ_(j=1) ^2 Σ_(i=1) ^j (i−1)i] =1+12+18+3[Σ_(i=1) ^1 (i−1)i+Σ_(i=1) ^2 (i−1)i] =1+12+18+6=37 a_5 =1+4×4+3×3×4+3[Σ_(i=1) ^1 (i−1)i+Σ_(i=1) ^2 (i−1)i+Σ_(i=1) ^3 (i−1)i] =1+16+36+3[0+2+(0+2+6)] =1+16+36+30=83 So the formula below satisfied a_1 to a_5 a_n =1+4(n−1)+3(n−2)(n−1)+3Σ_(j=1) ^(n−2) Σ_(i=1) ^j (i−1)i a_6 =1+4×5+3(4)(5)+3[(0∙1)+(0∙1+1∙2)+(0∙1+1∙2+2∙3)+(0∙1+1∙2+2∙3+3∙4)] =1+20+60+3[2+8+20] =1+20+60+90=171 see answer for a formula](Q3101.png)
$${a}_{\mathrm{1}} =\mathrm{1}\:{a}_{\mathrm{2}} =\mathrm{5}\:{a}_{\mathrm{3}} =\mathrm{15}\:{a}_{\mathrm{4}} =\mathrm{37}\:{a}_{\mathrm{5}} =\mathrm{83} \\ $$$${b}_{{n}} ={a}_{{n}} −{a}_{{n}+\mathrm{1}} \\ $$$${b}_{\mathrm{1}} =−\mathrm{4}\:\:{b}_{\mathrm{2}} =−\mathrm{10}\:{b}_{\mathrm{3}} =−\mathrm{22}\:{b}_{\mathrm{4}} =−\mathrm{46} \\ $$$${c}_{\mathrm{1}} =\mathrm{6}\:{c}_{\mathrm{2}} =\mathrm{12}\:{c}_{\mathrm{3}} =\mathrm{24} \\ $$$${c}_{{n}} ={b}_{{n}} −{b}_{{n}+\mathrm{1}} \\ $$$${d}_{\mathrm{1}} =−\mathrm{6}\:{d}_{\mathrm{2}} =−\mathrm{12} \\ $$$${d}_{{n}} ={c}_{{n}} −{c}_{{n}+\mathrm{1}} \\ $$$${d}_{{n}} =−\mathrm{6}{n} \\ $$$${c}_{{n}+\mathrm{1}} ={c}_{{n}} −{d}_{{n}} ={c}_{{n}} +\mathrm{6}{n}\:\left({c}_{\mathrm{1}} =\mathrm{6}\right) \\ $$$${c}_{\mathrm{2}} =\mathrm{6}+\mathrm{6}×\mathrm{1} \\ $$$${c}_{\mathrm{3}} =\mathrm{6}+\mathrm{6}×\mathrm{1}+\mathrm{6}×\mathrm{2} \\ $$$${c}_{{n}} =\mathrm{6}+\mathrm{3}\left({n}−\mathrm{1}\right){n} \\ $$$${b}_{{n}+\mathrm{1}} ={b}_{{n}} −{c}_{{n}} ={b}_{{n}} −\mathrm{6}−\mathrm{3}\left({n}−\mathrm{1}\right){n},\:{b}_{\mathrm{1}} =−\mathrm{4} \\ $$$${b}_{\mathrm{2}} =−\mathrm{4}−\mathrm{6}−\mathrm{3}\left(\mathrm{0}\right)\left(\mathrm{1}\right)=−\mathrm{10} \\ $$$${b}_{\mathrm{3}} =−\mathrm{4}−\mathrm{6}−\mathrm{3}\left(\mathrm{0}\right)\left(\mathrm{1}\right)−\mathrm{6}−\mathrm{3}\left(\mathrm{1}\right)\left(\mathrm{2}\right)=−\mathrm{22} \\ $$$${b}_{\mathrm{4}} =−\mathrm{4}−\mathrm{6}−\mathrm{3}\left(\mathrm{0}\right)\left(\mathrm{1}\right)−\mathrm{6}−\mathrm{3}\left(\mathrm{1}\right)\left(\mathrm{2}\right)−\mathrm{6}−\mathrm{3}\left(\mathrm{2}\right)\left(\mathrm{3}\right)=−\mathrm{46} \\ $$$${b}_{{n}} =−\mathrm{4}−\mathrm{6}\left({n}−\mathrm{1}\right)−\mathrm{3}\underset{{i}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left({i}−\mathrm{1}\right)\left({i}\right) \\ $$$${a}_{{n}+\mathrm{1}} ={a}_{{n}} −{b}_{{n}} \\ $$$${a}_{\mathrm{2}} ={a}_{\mathrm{1}} −{b}_{\mathrm{1}} =\mathrm{1}+\mathrm{4}+\mathrm{6}\left(\mathrm{0}\right)+\mathrm{3}\underset{{i}=\mathrm{1}} {\overset{\mathrm{0}} {\sum}}\left({i}−\mathrm{1}\right)\left({i}\right)=\mathrm{5} \\ $$$${a}_{\mathrm{3}} =\mathrm{1}+\mathrm{4}+\mathrm{6}\left(\mathrm{0}\right)+\mathrm{3}\underset{{i}=\mathrm{1}} {\overset{\mathrm{0}} {\sum}}\left({i}−\mathrm{1}\right)\left({i}\right)+\mathrm{4}+\mathrm{6}\left(\mathrm{1}\right)+\mathrm{3}\underset{{i}=\mathrm{1}} {\overset{\mathrm{1}} {\sum}}\left({i}−\mathrm{1}\right)\left({i}\right) \\ $$$$=\mathrm{1}+\mathrm{4}+\mathrm{0}+\mathrm{0}+\mathrm{4}+\mathrm{6}+\mathrm{3}\left(\mathrm{0}\right) \\ $$$${a}_{{n}} =\mathrm{1}+\mathrm{4}\left({n}−\mathrm{1}\right)+\mathrm{3}\left({n}−\mathrm{2}\right)\left({n}−\mathrm{1}\right)+\mathrm{3}\underset{{j}=\mathrm{1}} {\overset{{n}−\mathrm{2}} {\sum}}\underset{{i}=\mathrm{1}} {\overset{{j}} {\sum}}\left({i}−\mathrm{1}\right){i} \\ $$$${applying}\:{above}\:{formula} \\ $$$${a}_{\mathrm{1}} =\mathrm{1} \\ $$$${a}_{\mathrm{2}} =\mathrm{1}+\mathrm{4}+\mathrm{0}+\mathrm{0}=\mathrm{5} \\ $$$${a}_{\mathrm{3}} =\mathrm{1}+\mathrm{4}×\mathrm{2}+\mathrm{3}\left(\mathrm{1}\right)\left(\mathrm{2}\right)+\mathrm{3}\left[\underset{{i}=\mathrm{1}} {\overset{\mathrm{1}} {\sum}}\left({i}−\mathrm{1}\right){i}\right] \\ $$$$=\mathrm{1}+\mathrm{8}+\mathrm{6}+\mathrm{3}\left[\mathrm{0}\right]=\mathrm{15} \\ $$$${a}_{\mathrm{4}} =\mathrm{1}+\mathrm{4}×\mathrm{3}+\mathrm{3}\left(\mathrm{2}\right)\left(\mathrm{3}\right)+\mathrm{3}\left[\underset{{j}=\mathrm{1}} {\overset{\mathrm{2}} {\sum}}\underset{{i}=\mathrm{1}} {\overset{{j}} {\sum}}\left({i}−\mathrm{1}\right){i}\right] \\ $$$$=\mathrm{1}+\mathrm{12}+\mathrm{18}+\mathrm{3}\left[\underset{{i}=\mathrm{1}} {\overset{\mathrm{1}} {\sum}}\left({i}−\mathrm{1}\right){i}+\underset{{i}=\mathrm{1}} {\overset{\mathrm{2}} {\sum}}\left({i}−\mathrm{1}\right){i}\right] \\ $$$$=\mathrm{1}+\mathrm{12}+\mathrm{18}+\mathrm{6}=\mathrm{37} \\ $$$${a}_{\mathrm{5}} =\mathrm{1}+\mathrm{4}×\mathrm{4}+\mathrm{3}×\mathrm{3}×\mathrm{4}+\mathrm{3}\left[\underset{{i}=\mathrm{1}} {\overset{\mathrm{1}} {\sum}}\left({i}−\mathrm{1}\right){i}+\underset{{i}=\mathrm{1}} {\overset{\mathrm{2}} {\sum}}\left({i}−\mathrm{1}\right){i}+\underset{{i}=\mathrm{1}} {\overset{\mathrm{3}} {\sum}}\left({i}−\mathrm{1}\right){i}\right] \\ $$$$=\mathrm{1}+\mathrm{16}+\mathrm{36}+\mathrm{3}\left[\mathrm{0}+\mathrm{2}+\left(\mathrm{0}+\mathrm{2}+\mathrm{6}\right)\right] \\ $$$$=\mathrm{1}+\mathrm{16}+\mathrm{36}+\mathrm{30}=\mathrm{83} \\ $$$${S}\mathrm{o}\:\mathrm{the}\:\mathrm{formula}\:\mathrm{below}\:\mathrm{satisfied}\:{a}_{\mathrm{1}} \:\mathrm{to}\:{a}_{\mathrm{5}} \\ $$$${a}_{{n}} =\mathrm{1}+\mathrm{4}\left({n}−\mathrm{1}\right)+\mathrm{3}\left({n}−\mathrm{2}\right)\left({n}−\mathrm{1}\right)+\mathrm{3}\underset{{j}=\mathrm{1}} {\overset{{n}−\mathrm{2}} {\sum}}\underset{{i}=\mathrm{1}} {\overset{{j}} {\sum}}\left({i}−\mathrm{1}\right){i} \\ $$$${a}_{\mathrm{6}} =\mathrm{1}+\mathrm{4}×\mathrm{5}+\mathrm{3}\left(\mathrm{4}\right)\left(\mathrm{5}\right)+\mathrm{3}\left[\left(\mathrm{0}\centerdot\mathrm{1}\right)+\left(\mathrm{0}\centerdot\mathrm{1}+\mathrm{1}\centerdot\mathrm{2}\right)+\left(\mathrm{0}\centerdot\mathrm{1}+\mathrm{1}\centerdot\mathrm{2}+\mathrm{2}\centerdot\mathrm{3}\right)+\left(\mathrm{0}\centerdot\mathrm{1}+\mathrm{1}\centerdot\mathrm{2}+\mathrm{2}\centerdot\mathrm{3}+\mathrm{3}\centerdot\mathrm{4}\right)\right] \\ $$$$=\mathrm{1}+\mathrm{20}+\mathrm{60}+\mathrm{3}\left[\mathrm{2}+\mathrm{8}+\mathrm{20}\right] \\ $$$$=\mathrm{1}+\mathrm{20}+\mathrm{60}+\mathrm{90}=\mathrm{171} \\ $$$${see}\:{answer}\:{for}\:{a}\:{formula} \\ $$
Answered by Yozzi last updated on 02/Dec/15

$$\mathrm{6}×\left(\mathrm{1}−\mathrm{1}\right)−\left(−\mathrm{1}\right)=\mathrm{1} \\ $$$$\mathrm{6}\left(\mathrm{2}−\mathrm{1}\right)−\mathrm{1}=\mathrm{5} \\ $$$$\mathrm{6}×\left(\mathrm{4}−\mathrm{1}\right)−\mathrm{3}=\mathrm{15} \\ $$$$\mathrm{6}×\left(\mathrm{8}−\mathrm{1}\right)−\mathrm{5}=\mathrm{37} \\ $$$$\mathrm{6}×\left(\mathrm{16}−\mathrm{1}\right)−\mathrm{7}=\mathrm{83} \\ $$$${a}_{{n}} =\mathrm{6}\left(\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{1}\right)−\mathrm{2}{n}+\mathrm{3} \\ $$$$\Rightarrow{a}_{\mathrm{1}} =\mathrm{6}\left(\mathrm{1}−\mathrm{1}\right)−\mathrm{2}+\mathrm{3}=\mathrm{1} \\ $$$${a}_{\mathrm{2}} =\mathrm{6}\left(\mathrm{2}−\mathrm{1}\right)−\mathrm{4}+\mathrm{3}=\mathrm{6}−\mathrm{1}=\mathrm{5} \\ $$$${a}_{\mathrm{3}} =\mathrm{6}\left(\mathrm{3}\right)−\mathrm{6}+\mathrm{3}=\mathrm{15} \\ $$$${a}_{\mathrm{4}} =\mathrm{42}−\mathrm{8}+\mathrm{3}=\mathrm{42}−\mathrm{5}=\mathrm{37} \\ $$$${a}_{\mathrm{5}} =\mathrm{6}×\mathrm{15}−\mathrm{10}+\mathrm{3}=\mathrm{83} \\ $$$${The}\:{general}\:{term}\:{of}\:{the}\:{sequence}\:\left\{{b}_{{n}} \right\} \\ $$$${is}\:{then} \\ $$$${b}_{{n}} =\frac{\mathrm{6}\left(\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{1}\right)−\mathrm{2}{n}+\mathrm{3}}{\mathrm{2}^{{n}} }\:{n}\geqslant\mathrm{1} \\ $$$$ \\ $$
Commented by Yozzi last updated on 02/Dec/15
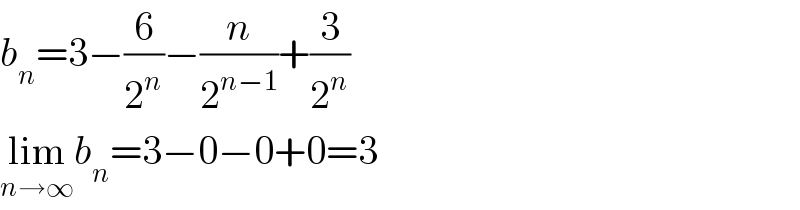
$${b}_{{n}} =\mathrm{3}−\frac{\mathrm{6}}{\mathrm{2}^{{n}} }−\frac{{n}}{\mathrm{2}^{{n}−\mathrm{1}} }+\frac{\mathrm{3}}{\mathrm{2}^{{n}} } \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{b}_{{n}} =\mathrm{3}−\mathrm{0}−\mathrm{0}+\mathrm{0}=\mathrm{3} \\ $$
Commented by Yozzi last updated on 02/Dec/15

$${Nice}\:{work}\:{Mr}.\:{Ahmad}!\:{It}\:{took}\:{a} \\ $$$${while}\:{for}\:{me}\:{to}\:{make}\:{such}\:{observations}. \\ $$$${It}\:{would}\:{be}\:{suitable}\:{if}\:{the}\:{formula} \\ $$$${I}\:{proposed}\:{is}\:{proved}\:{by}\:{induction} \\ $$$${on}\:{n}. \\ $$$$ \\ $$
Commented by RasheedAhmad last updated on 02/Dec/15

$$\mathcal{SUPER}!\:\mathcal{D}{on}'{t}\:{have}\:{words}!! \\ $$$${Within}\:{unexpected}\:{short}\:{time}! \\ $$$$ \\ $$$${This}\:{question}\:{is}\:{actually}\:{very} \\ $$$${closely}\:{related}\:{to}\:{Q}\mathrm{2941}. \\ $$$${The}\:{terms}\:{are}\:{actually}\:{sums}\:{of} \\ $$$$\mathrm{1},\:\mathrm{2},\:\mathrm{3},...{terms}\:{of}\:{the}\:{series}\:{of} \\ $$$${Q}\mathrm{2941}.\:{Your}\:{answer}\:{is}\:{sum}\:{of} \\ $$$${n}\:{terms}.\:{I}\:{think}\:{the}\:{Q}\mathrm{2941}\:{can} \\ $$$${also}\:{be}\:{solved}\:{now}\:{in}\:{a}\:{different}\: \\ $$$${way}. \\ $$
Commented by 123456 last updated on 02/Dec/15

$${s}_{{n}} =\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} \\ $$$${a}_{{n}+\mathrm{1}} ={s}_{{n}+\mathrm{1}} −{s}_{{n}} \\ $$
Commented by Rasheed Soomro last updated on 03/Dec/15
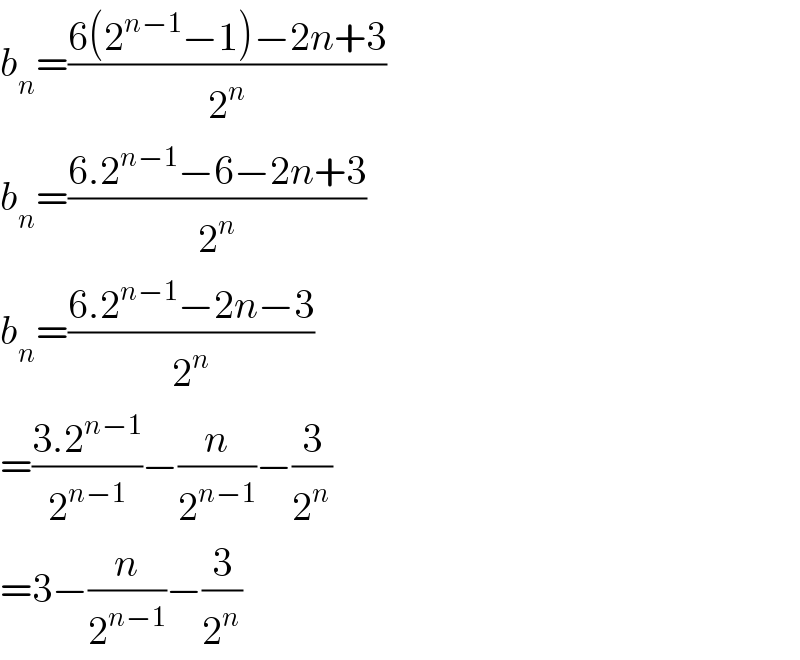
$${b}_{{n}} =\frac{\mathrm{6}\left(\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{1}\right)−\mathrm{2}{n}+\mathrm{3}}{\mathrm{2}^{{n}} } \\ $$$${b}_{{n}} =\frac{\mathrm{6}.\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{6}−\mathrm{2}{n}+\mathrm{3}}{\mathrm{2}^{{n}} } \\ $$$${b}_{{n}} =\frac{\mathrm{6}.\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{2}{n}−\mathrm{3}}{\mathrm{2}^{{n}} } \\ $$$$=\frac{\mathrm{3}.\mathrm{2}^{{n}−\mathrm{1}} }{\mathrm{2}^{{n}−\mathrm{1}} }−\frac{{n}}{\mathrm{2}^{{n}−\mathrm{1}} }−\frac{\mathrm{3}}{\mathrm{2}^{{n}} } \\ $$$$=\mathrm{3}−\frac{{n}}{\mathrm{2}^{{n}−\mathrm{1}} }−\frac{\mathrm{3}}{\mathrm{2}^{{n}} } \\ $$
Commented by Rasheed Soomro last updated on 03/Dec/15

$${Thanks}!\:{My}\:{answer}\:{was}\:{not}\:{matching}\:{with} \\ $$$${your}\:{answer}.{For}\:{testing}\:{I}\:{calculated}\:{wrongly}\: \\ $$$$\mathrm{2}{nd}\:{term}\:{which}\:{also}\:{didn}'{t}\:{match}...{but}\:{now} \\ $$$${it}'{s}\:{all}\:{right}. \\ $$$$\:\:\:\:\:\:{But}\:{then}\:{your}\:{answer}\:{in}\:{earlier}\:{comment} \\ $$$${needs}\:{to}\:{simplify}\:{a}\:{bit}\:{more}. \\ $$
Commented by Yozzi last updated on 03/Dec/15
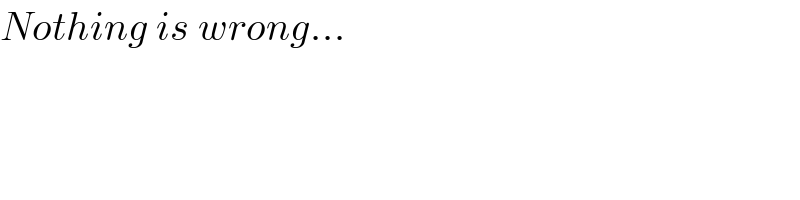
$${Nothing}\:{is}\:{wrong}... \\ $$
Commented by prakash jain last updated on 04/Dec/15
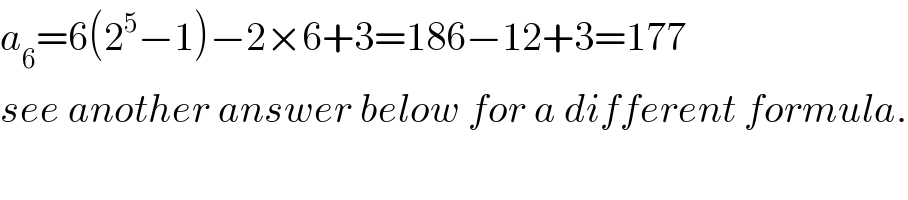
$${a}_{\mathrm{6}} =\mathrm{6}\left(\mathrm{2}^{\mathrm{5}} −\mathrm{1}\right)−\mathrm{2}×\mathrm{6}+\mathrm{3}=\mathrm{186}−\mathrm{12}+\mathrm{3}=\mathrm{177} \\ $$$${see}\:{another}\:{answer}\:{below}\:{for}\:{a}\:{different}\:{formula}. \\ $$
Answered by prakash jain last updated on 04/Dec/15
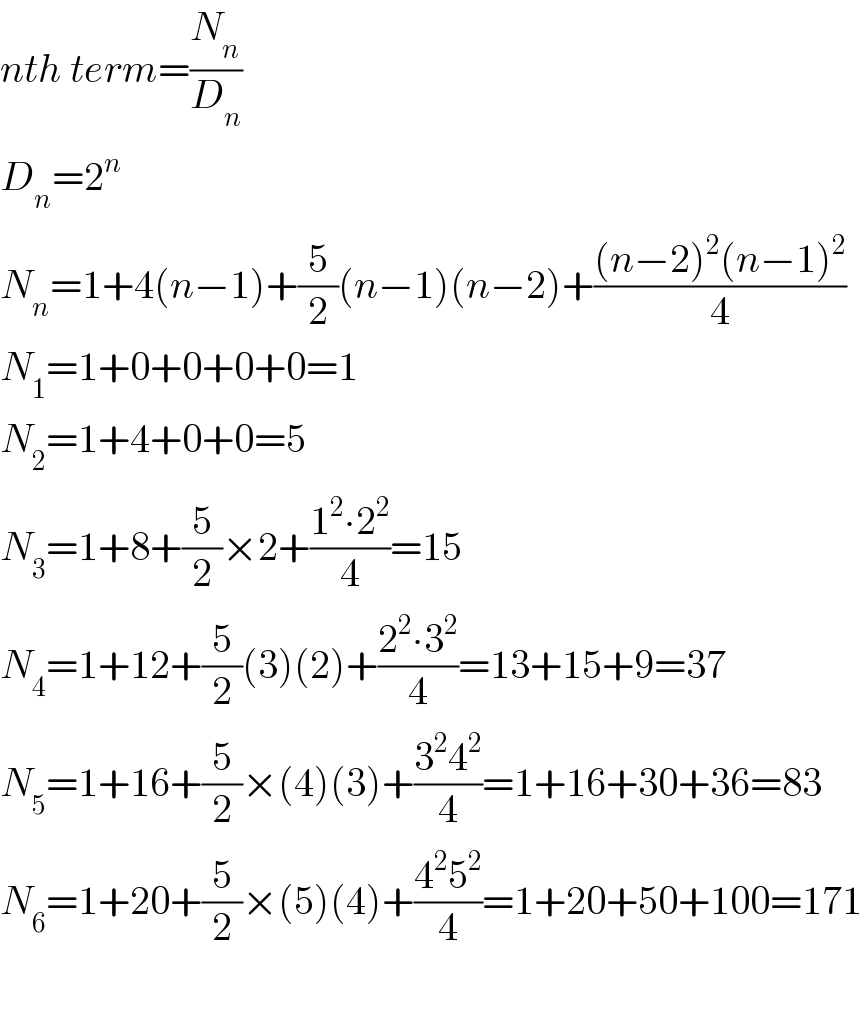
$${nth}\:{term}=\frac{{N}_{{n}} }{{D}_{{n}} } \\ $$$${D}_{{n}} =\mathrm{2}^{{n}} \\ $$$${N}_{{n}} =\mathrm{1}+\mathrm{4}\left({n}−\mathrm{1}\right)+\frac{\mathrm{5}}{\mathrm{2}}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)+\frac{\left({n}−\mathrm{2}\right)^{\mathrm{2}} \left({n}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$${N}_{\mathrm{1}} =\mathrm{1}+\mathrm{0}+\mathrm{0}+\mathrm{0}+\mathrm{0}=\mathrm{1} \\ $$$${N}_{\mathrm{2}} =\mathrm{1}+\mathrm{4}+\mathrm{0}+\mathrm{0}=\mathrm{5} \\ $$$${N}_{\mathrm{3}} =\mathrm{1}+\mathrm{8}+\frac{\mathrm{5}}{\mathrm{2}}×\mathrm{2}+\frac{\mathrm{1}^{\mathrm{2}} \centerdot\mathrm{2}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{15} \\ $$$${N}_{\mathrm{4}} =\mathrm{1}+\mathrm{12}+\frac{\mathrm{5}}{\mathrm{2}}\left(\mathrm{3}\right)\left(\mathrm{2}\right)+\frac{\mathrm{2}^{\mathrm{2}} \centerdot\mathrm{3}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{13}+\mathrm{15}+\mathrm{9}=\mathrm{37} \\ $$$${N}_{\mathrm{5}} =\mathrm{1}+\mathrm{16}+\frac{\mathrm{5}}{\mathrm{2}}×\left(\mathrm{4}\right)\left(\mathrm{3}\right)+\frac{\mathrm{3}^{\mathrm{2}} \mathrm{4}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{1}+\mathrm{16}+\mathrm{30}+\mathrm{36}=\mathrm{83} \\ $$$${N}_{\mathrm{6}} =\mathrm{1}+\mathrm{20}+\frac{\mathrm{5}}{\mathrm{2}}×\left(\mathrm{5}\right)\left(\mathrm{4}\right)+\frac{\mathrm{4}^{\mathrm{2}} \mathrm{5}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{1}+\mathrm{20}+\mathrm{50}+\mathrm{100}=\mathrm{171} \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 05/Dec/15

$$\mathcal{N}{ot}\:{only}\:{you}\:{have}\:\boldsymbol{\mathcal{K}{nowledge}}\:\:{but}\:{also}\:{a}\:\boldsymbol{\mathcal{N}{ice}}\:{way}\:{to} \\ $$$${convey}\:{it}! \\ $$
