
Question and Answers Forum
Question Number 30182 by abdo imad last updated on 17/Feb/18
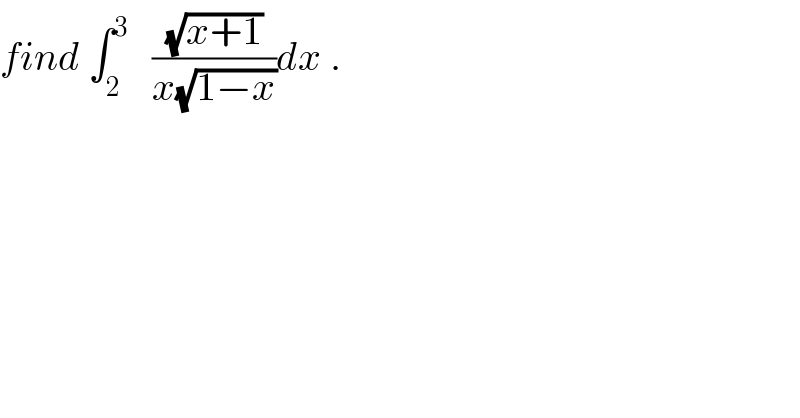
Commented by abdo imad last updated on 21/Feb/18
![let put (√((x+1)/(x−1))) =t ⇔((x+1)/(x−1)) =t^2 ⇔x+1=−t^2 +t^2 x⇔ (1−t^2 )x=−t^2 −1 ⇔x= ((−t^2 −1)/(−t^2 +1))=((t^2 +1)/(t^2 −1))=1+(2/(t^2 −1))⇒ (dx/dt) =((−4t)/((t^2 −1)^2 )) ⇒I= ∫_(√3) ^(√2) t ((t^2 −1)/(t^2 +1)) ((−4t)/((t^2 −1)^2 ))dt =4 ∫_(√2) ^(√3) (t^2 /((t^2 +1)(t^2 −1)))dt= 4 ∫_(√2) ^(√3) ((t^2 −1+1)/((t^2 +1)(t^2 −1)))dt =4 ∫_(√2) ^(√3) (dt/(t^2 +1)) +4 ∫_(√2) ^(√3) (dt/((t^2 +1)(t^2 −1))) we have ∫_(√2) ^(√3) (dt/(1+t^2 ))=arctan((√3)) −arctan((√2)) and ∫_(√2) ^(√3) (dt/((t^2 +1)(t^2 −1)))=(1/2)∫_(√2) ^(√3) ( (1/(t^2 −1)) −(1/(t^2 +1)))dt =(1/2) ∫_(√2) ^(√3) (dt/(t^2 −1)) −(1/2) (arctan((√(3))) −arctan(√2))) =(1/2)∫_(√2) ^(√3) ((1/(t−1)) −(1/(t+1)))dt −(1/2)(....) =(1/2)[ln∣((t−1)/(t+1))∣]_(√2) ^(√3) −(1/2)(...) ⇒ I=4(artan((√3))−arctan((√2))) +2 ∫_(√2) ^(√3) (dt/(t^2 −1))dt −2(arctan((√3))−arctan((√2))) =2(arctan((√3))−arctan((√2))) +ln∣(((√3) −1)/((√3)+1))∣−ln∣(((√2) −1)/((√2) +1))∣ .](Q30345.png)
Commented by abdo imad last updated on 21/Feb/18
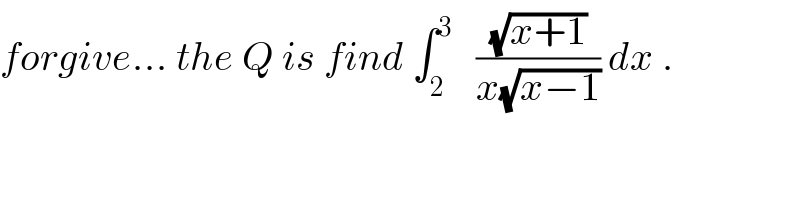
| ||
Question and Answers Forum | ||
Question Number 30182 by abdo imad last updated on 17/Feb/18 | ||
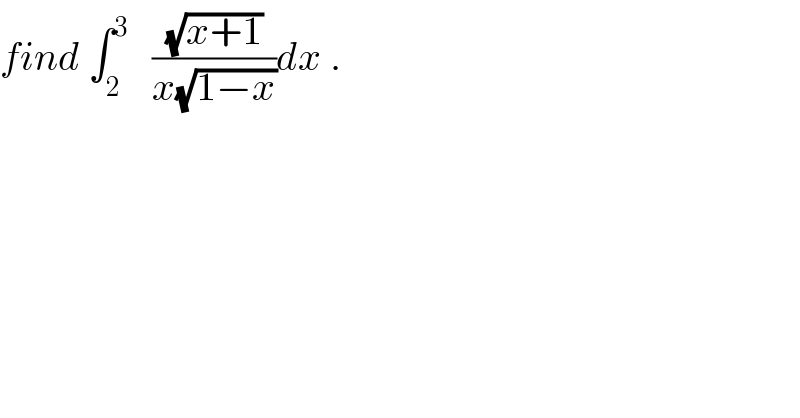 | ||
Commented by abdo imad last updated on 21/Feb/18 | ||
![let put (√((x+1)/(x−1))) =t ⇔((x+1)/(x−1)) =t^2 ⇔x+1=−t^2 +t^2 x⇔ (1−t^2 )x=−t^2 −1 ⇔x= ((−t^2 −1)/(−t^2 +1))=((t^2 +1)/(t^2 −1))=1+(2/(t^2 −1))⇒ (dx/dt) =((−4t)/((t^2 −1)^2 )) ⇒I= ∫_(√3) ^(√2) t ((t^2 −1)/(t^2 +1)) ((−4t)/((t^2 −1)^2 ))dt =4 ∫_(√2) ^(√3) (t^2 /((t^2 +1)(t^2 −1)))dt= 4 ∫_(√2) ^(√3) ((t^2 −1+1)/((t^2 +1)(t^2 −1)))dt =4 ∫_(√2) ^(√3) (dt/(t^2 +1)) +4 ∫_(√2) ^(√3) (dt/((t^2 +1)(t^2 −1))) we have ∫_(√2) ^(√3) (dt/(1+t^2 ))=arctan((√3)) −arctan((√2)) and ∫_(√2) ^(√3) (dt/((t^2 +1)(t^2 −1)))=(1/2)∫_(√2) ^(√3) ( (1/(t^2 −1)) −(1/(t^2 +1)))dt =(1/2) ∫_(√2) ^(√3) (dt/(t^2 −1)) −(1/2) (arctan((√(3))) −arctan(√2))) =(1/2)∫_(√2) ^(√3) ((1/(t−1)) −(1/(t+1)))dt −(1/2)(....) =(1/2)[ln∣((t−1)/(t+1))∣]_(√2) ^(√3) −(1/2)(...) ⇒ I=4(artan((√3))−arctan((√2))) +2 ∫_(√2) ^(√3) (dt/(t^2 −1))dt −2(arctan((√3))−arctan((√2))) =2(arctan((√3))−arctan((√2))) +ln∣(((√3) −1)/((√3)+1))∣−ln∣(((√2) −1)/((√2) +1))∣ .](Q30345.png) | ||
Commented by abdo imad last updated on 21/Feb/18 | ||
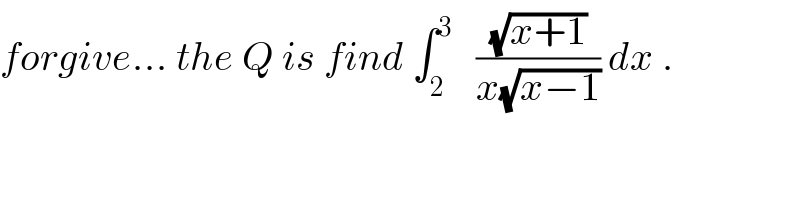 | ||