
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 30214 by abdo imad last updated on 18/Feb/18
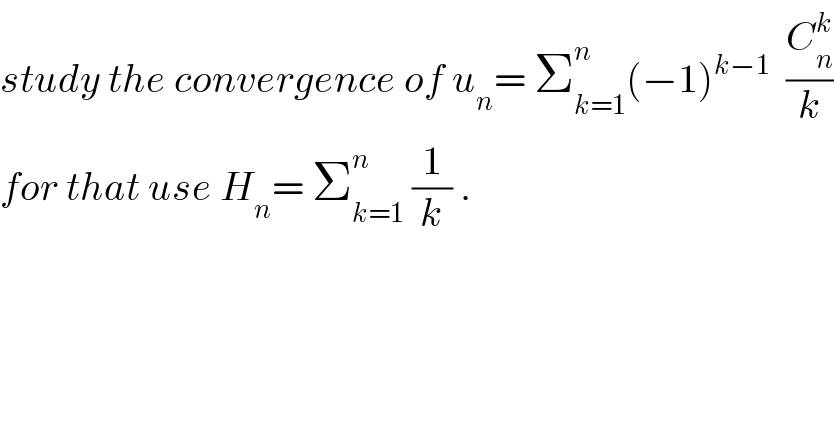
Commented by prof Abdo imad last updated on 22/Feb/18
![let condider p(x)= Σ_(k=1) ^n (−1)^(k−1) (C_n ^k /k) x^k we have p^′ (x)= Σ_(k=1) ^n C_n ^k (−1)^(k−1) x^(k−1) =((−1)/x)Σ_(k=1) ^n C_n ^k (−1)^k x^k =−(1/x)(Σ_(k=0) ^n (−1)^k x^k −1) =(1/x)( 1−(1−x)^n )=((1−(1−x)^n )/x) ⇒ p(x)= ∫_0 ^x ((1−(1−t)^n )/t)dt +λ but λ=p(0)=0⇒ p(x)= ∫_0 ^x ((1−(1−t)^n )/t)dt and u_n =p(1)⇒ u_n = ∫_0 ^1 ((1−(1−t)^n )/t)dt = = ∫_0 ^1 ((1+(1−t) +(1−t)^2 +....(1−t)^(n−1) )dt =∫_0 ^1 Σ_(k=0) ^(n−1) (1−t)^k dt= Σ_(k=0) ^(n−1) ∫_0 ^1 (1−t)^k dt =Σ_(k=0) ^(n−1) [((−1)/(k+1))(1−t)^(k+1) ]_0 ^1 =Σ_(k=0) ^(n−1) (1/(k+1)) = H_n but H_n ∼ln(n) for n→∞ ⇒lim_(n→∞) u_n =+∞.](Q30446.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 30214 by abdo imad last updated on 18/Feb/18 | ||
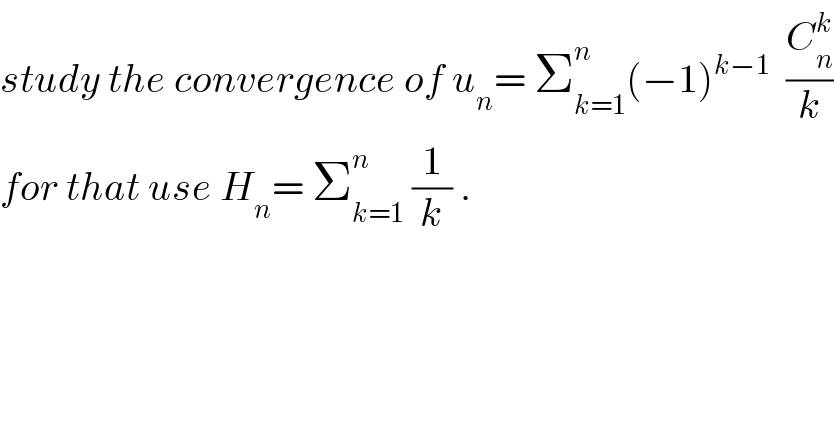 | ||
Commented by prof Abdo imad last updated on 22/Feb/18 | ||
![let condider p(x)= Σ_(k=1) ^n (−1)^(k−1) (C_n ^k /k) x^k we have p^′ (x)= Σ_(k=1) ^n C_n ^k (−1)^(k−1) x^(k−1) =((−1)/x)Σ_(k=1) ^n C_n ^k (−1)^k x^k =−(1/x)(Σ_(k=0) ^n (−1)^k x^k −1) =(1/x)( 1−(1−x)^n )=((1−(1−x)^n )/x) ⇒ p(x)= ∫_0 ^x ((1−(1−t)^n )/t)dt +λ but λ=p(0)=0⇒ p(x)= ∫_0 ^x ((1−(1−t)^n )/t)dt and u_n =p(1)⇒ u_n = ∫_0 ^1 ((1−(1−t)^n )/t)dt = = ∫_0 ^1 ((1+(1−t) +(1−t)^2 +....(1−t)^(n−1) )dt =∫_0 ^1 Σ_(k=0) ^(n−1) (1−t)^k dt= Σ_(k=0) ^(n−1) ∫_0 ^1 (1−t)^k dt =Σ_(k=0) ^(n−1) [((−1)/(k+1))(1−t)^(k+1) ]_0 ^1 =Σ_(k=0) ^(n−1) (1/(k+1)) = H_n but H_n ∼ln(n) for n→∞ ⇒lim_(n→∞) u_n =+∞.](Q30446.png) | ||