Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 3022 by Rasheed Soomro last updated on 03/Dec/15

Determine 1+2^(1/2) +3^(1/3) +...

$$\mathrm{Determine} \\ $$$$\mathrm{1}+\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} +... \\ $$

Commented by prakash jain last updated on 04/Dec/15

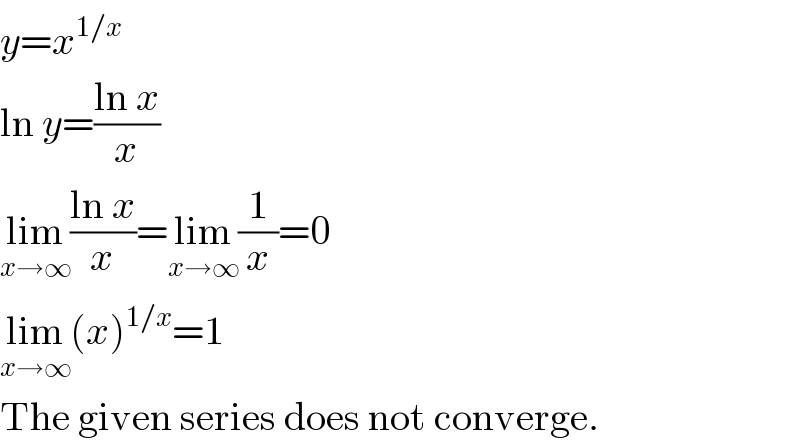
y=x^(1/x) ln y=((ln x)/x) lim_(x→∞) ((ln x)/x)=lim_(x→∞) (1/x)=0 lim_(x→∞) (x)^(1/x) =1 The given series does not converge.

$${y}={x}^{\mathrm{1}/{x}} \\ $$$$\mathrm{ln}\:{y}=\frac{\mathrm{ln}\:{x}}{{x}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{ln}\:{x}}{{x}}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}=\mathrm{0} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({x}\right)^{\mathrm{1}/{x}} =\mathrm{1} \\ $$$$\mathrm{The}\:\mathrm{given}\:\mathrm{series}\:\mathrm{does}\:\mathrm{not}\:\mathrm{converge}. \\ $$

Commented by Filup last updated on 03/Dec/15

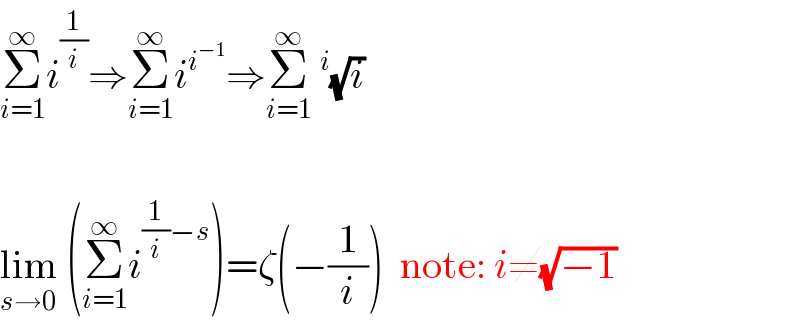
Σ_(i=1) ^∞ i^(1/i) ⇒Σ_(i=1) ^∞ i^i^(−1) ⇒Σ_(i=1) ^∞ ^i (√i) lim_(s→0) (Σ_(i=1) ^∞ i^((1/i)−s) )=ζ(−(1/i)) note: i≠(√(−1))

$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{i}^{\frac{\mathrm{1}}{{i}}} \Rightarrow\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{i}^{{i}^{−\mathrm{1}} } \Rightarrow\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\:^{{i}} \sqrt{{i}} \\ $$$$ \\ $$$$\underset{{s}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{i}^{\frac{\mathrm{1}}{{i}}−{s}} \right)=\zeta\left(−\frac{\mathrm{1}}{{i}}\right)\:\:\mathrm{note}:\:{i}\neq\sqrt{−\mathrm{1}} \\ $$

Commented by Rasheed Soomro last updated on 03/Dec/15

Didn′t understand. Try again please!

$$\mathcal{D}{idn}'{t}\:{understand}.\:\mathcal{T}{ry}\:{again}\:{please}! \\ $$

Commented by Filup last updated on 04/Dec/15

Because the given serious converges to value 1 (i^(−i) not S), the series at i→∞ is about ...1+1+1+1+... with each value getting closer to 1. This makes the series not limit to a single value. Hence showing evidence that ζ(−(1/i))=∞ and S_2 in some cases

$$\mathrm{Because}\:\mathrm{the}\:\mathrm{given}\:\mathrm{serious}\:\mathrm{converges} \\ $$$$\mathrm{to}\:\mathrm{value}\:\mathrm{1}\:\left({i}^{−{i}} \:\:{not}\:{S}\right),\:\mathrm{the}\:\mathrm{series}\:\mathrm{at}\:{i}\rightarrow\infty \\ $$$$\mathrm{is}\:\mathrm{about}\:\:...\mathrm{1}+\mathrm{1}+\mathrm{1}+\mathrm{1}+... \\ $$$$\mathrm{with}\:\mathrm{each}\:\mathrm{value}\:\mathrm{getting}\:\mathrm{closer}\:\mathrm{to}\:\mathrm{1}. \\ $$$$\mathrm{This}\:\mathrm{makes}\:\mathrm{the}\:\mathrm{series}\:\mathrm{not}\:\mathrm{limit}\:\mathrm{to}\:\mathrm{a}\:\mathrm{single} \\ $$$$\mathrm{value}. \\ $$$$ \\ $$$$\mathrm{Hence}\:\mathrm{showing}\:\mathrm{evidence}\:\mathrm{that}\:\zeta\left(−\frac{\mathrm{1}}{{i}}\right)=\infty \\ $$$$\mathrm{and}\:{S}_{\mathrm{2}} \:\mathrm{in}\:\mathrm{some}\:\mathrm{cases} \\ $$

Commented by prakash jain last updated on 04/Dec/15

A series S=Σ_(n=1) ^∞ a_n converges only lim_(n→∞) a_n =0. This is necessary condition.

$$\mathrm{A}\:\mathrm{series}\:\mathrm{S}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{a}_{{n}} \:\mathrm{converges}\:\mathrm{only}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}_{{n}} =\mathrm{0}. \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{necessary}\:\mathrm{condition}. \\ $$

Commented by Rasheed Soomro last updated on 04/Dec/15

ThankS!

$$\mathcal{T}\boldsymbol{{hank}}{S}! \\ $$

Answered by Filup last updated on 03/Dec/15

for S=ζ(−s), S→∞ There maybe be an analytical approach such as ζ(−1)=ΣN^+ =−(1/(12)) My unproven solution would be that for S=Σ_(i=1) ^∞ i^(1/i) =ζ(−(1/i)) as i→∞, S→∞ So, I would suggest that S={∞, S_2 } Where S_2 is an analytical solution

$$\mathrm{for}\:{S}=\zeta\left(−{s}\right),\:{S}\rightarrow\infty \\ $$$$\mathrm{There}\:\mathrm{maybe}\:\mathrm{be}\:\mathrm{an}\:\mathrm{analytical} \\ $$$$\mathrm{approach}\:\mathrm{such}\:\mathrm{as}\:\zeta\left(−\mathrm{1}\right)=\Sigma\mathbb{N}^{+} =−\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$ \\ $$$$\mathrm{My}\:\mathrm{unproven}\:\mathrm{solution}\:\mathrm{would}\:\mathrm{be}\:\mathrm{that} \\ $$$$\mathrm{for}\:{S}=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{i}^{\frac{\mathrm{1}}{{i}}} =\zeta\left(−\frac{\mathrm{1}}{{i}}\right) \\ $$$${as}\:\:{i}\rightarrow\infty,\:{S}\rightarrow\infty \\ $$$$ \\ $$$$\mathrm{So},\:\mathrm{I}\:\mathrm{would}\:\mathrm{suggest}\:\mathrm{that} \\ $$$${S}=\left\{\infty,\:{S}_{\mathrm{2}} \right\} \\ $$$$\mathrm{Where}\:\:{S}_{\mathrm{2}} \:\:\mathrm{is}\:\mathrm{an}\:\mathrm{analytical}\:\mathrm{solution} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com