Question Number 30233 by ajfour last updated on 18/Feb/18
Commented by ajfour last updated on 18/Feb/18
$${Find}\:{maximum}\:{area}\:{of}\:{quadrilateral} \\ $$$${ABCD}\:\:{if}\:\:{sides}\:{AB},\:{BC},\:{CD},\:{DA} \\ $$$${be}\:{a},\:{b},\:{c},\:{d}\:\:{respectively},\:{with} \\ $$$$\:\:{a}\:<\:{b}\:<\:{c}\:<\:{d}\:. \\ $$
Answered by mrW2 last updated on 19/Feb/18
![let ∠B=α, ∠D=β<α a^2 +b^2 −2ab cos α=c^2 +d^2 −2cd cos β ab sin α=cd sin β (dβ/dα) A=(1/2)(ab sin α+cd sin β) (dA/dα)=(1/2)[ab cos α+cd cos β (((ab sin α)/(cd sin β)))] (dA/dα)=(1/2)ab (cos α+((sin α)/(tan β)))=0 ⇒tan α=−tan β ⇒α=π−β or α+β=π⇒cyclic! a^2 +b^2 +2ab cos β=c^2 +d^2 −2cd cos β 2(ab+cd)cos β=c^2 +d^2 −a^2 −b^2 ⇒cos β=((c^2 +d^2 −a^2 −b^2 )/(2(ab+cd))) ⇒sin β=(√(1−(((c^2 +d^2 −a^2 −b^2 )^2 )/(4(ab+cd)^2 )))) =((√((2ab+2cd+c^2 +d^2 −a^2 −b^2 )(2ab+2cd−c^2 −d^2 +a^2 +b^2 )))/(2(ab+cd))) ⇒sin β =((√([(c+d)^2 −(a−b)^2 ][(a+b)^2 −(c−d)^2 ]))/(2(ab+cd))) ⇒sin β =((√((−a+b+c+d)(a−b+c+d)(a+b−c+d)(a+b+c−d)))/(2(ab+cd))) ⇒sin α=sin β A_(max) =(1/2)(ab+cd) sin β=(1/2)(ab+cd)×((√((−a+b+c+d)(a−b+c+d)(a+b−c+d)(a+b+c−d)))/(2(ab+cd))) ⇒A_(max) =(1/4)(√((−a+b+c+d)(a−b+c+d)(a+b−c+d)(a+b+c−d))) with s=((a+b+c+d)/2) ⇒A_(max) =(√((s−a)(s−b)(s−c)(s−d)))](Q30237.png)
$${let}\:\angle{B}=\alpha,\:\angle{D}=\beta<\alpha \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\alpha={c}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{cd}\:\mathrm{cos}\:\beta \\ $$$${ab}\:\mathrm{sin}\:\alpha={cd}\:\mathrm{sin}\:\beta\:\frac{{d}\beta}{{d}\alpha} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}\left({ab}\:\mathrm{sin}\:\alpha+{cd}\:\mathrm{sin}\:\beta\right) \\ $$$$\frac{{dA}}{{d}\alpha}=\frac{\mathrm{1}}{\mathrm{2}}\left[{ab}\:\mathrm{cos}\:\alpha+{cd}\:\mathrm{cos}\:\beta\:\left(\frac{{ab}\:\mathrm{sin}\:\alpha}{{cd}\:\mathrm{sin}\:\beta}\right)\right] \\ $$$$\frac{{dA}}{{d}\alpha}=\frac{\mathrm{1}}{\mathrm{2}}{ab}\:\left(\mathrm{cos}\:\alpha+\frac{\mathrm{sin}\:\alpha}{\mathrm{tan}\:\beta}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha=−\mathrm{tan}\:\beta \\ $$$$\Rightarrow\alpha=\pi−\beta\:{or}\:\alpha+\beta=\pi\Rightarrow{cyclic}! \\ $$$$ \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}\:\mathrm{cos}\:\beta={c}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{cd}\:\mathrm{cos}\:\beta \\ $$$$\mathrm{2}\left({ab}+{cd}\right)\mathrm{cos}\:\beta={c}^{\mathrm{2}} +{d}^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{cos}\:\beta=\frac{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}\left({ab}+{cd}\right)} \\ $$$$\Rightarrow\mathrm{sin}\:\beta=\sqrt{\mathrm{1}−\frac{\left({c}^{\mathrm{2}} +{d}^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{4}\left({ab}+{cd}\right)^{\mathrm{2}} }}\:=\frac{\sqrt{\left(\mathrm{2}{ab}+\mathrm{2}{cd}+{c}^{\mathrm{2}} +{d}^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left(\mathrm{2}{ab}+\mathrm{2}{cd}−{c}^{\mathrm{2}} −{d}^{\mathrm{2}} +{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}}{\mathrm{2}\left({ab}+{cd}\right)} \\ $$$$\Rightarrow\mathrm{sin}\:\beta\:=\frac{\sqrt{\left[\left({c}+{d}\right)^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} \right]\left[\left({a}+{b}\right)^{\mathrm{2}} −\left({c}−{d}\right)^{\mathrm{2}} \right]}}{\mathrm{2}\left({ab}+{cd}\right)} \\ $$$$\Rightarrow\mathrm{sin}\:\beta\:=\frac{\sqrt{\left(−{a}+{b}+{c}+{d}\right)\left({a}−{b}+{c}+{d}\right)\left({a}+{b}−{c}+{d}\right)\left({a}+{b}+{c}−{d}\right)}}{\mathrm{2}\left({ab}+{cd}\right)} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\mathrm{sin}\:\beta \\ $$$${A}_{{max}} =\frac{\mathrm{1}}{\mathrm{2}}\left({ab}+{cd}\right)\:\mathrm{sin}\:\beta=\frac{\mathrm{1}}{\mathrm{2}}\left({ab}+{cd}\right)×\frac{\sqrt{\left(−{a}+{b}+{c}+{d}\right)\left({a}−{b}+{c}+{d}\right)\left({a}+{b}−{c}+{d}\right)\left({a}+{b}+{c}−{d}\right)}}{\mathrm{2}\left({ab}+{cd}\right)} \\ $$$$\Rightarrow{A}_{{max}} =\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\left(−{a}+{b}+{c}+{d}\right)\left({a}−{b}+{c}+{d}\right)\left({a}+{b}−{c}+{d}\right)\left({a}+{b}+{c}−{d}\right)} \\ $$$${with}\:{s}=\frac{{a}+{b}+{c}+{d}}{\mathrm{2}} \\ $$$$\Rightarrow{A}_{{max}} =\sqrt{\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)\left({s}−{d}\right)} \\ $$
Commented by ajfour last updated on 19/Feb/18
$${Wonderful}\:{answer}.\:{Thank}\:{you}\:{Sir}. \\ $$
Commented by mrW2 last updated on 19/Feb/18
$${if}\:{perimeter}\:{of}\:{quadrilateral}\:{is}\:{l},\:{find} \\ $$$${the}\:{maximal}\:{possible}\:{area}\:{of}\:{it}. \\ $$$${let}\:{the}\:{first}\:{three}\:{side}\:{lengths}\:{are}\:{x},{y},{z}.\: \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\left({l}−\mathrm{2}{x}\right)\left({l}−\mathrm{2}{y}\right)\left({l}−\mathrm{2}{z}\right)\left(\mathrm{2}{x}+\mathrm{2}{y}+\mathrm{2}{z}−{l}\right)} \\ $$$${f}\left({x},{y},{z}\right)=\sqrt{\left({l}−\mathrm{2}{x}\right)\left({l}−\mathrm{2}{y}\right)\left({l}−\mathrm{2}{z}\right)\left(\mathrm{2}{x}+\mathrm{2}{y}+\mathrm{2}{z}−{l}\right)} \\ $$$$\frac{\partial{f}}{\partial{x}}=\frac{−\mathrm{2}\left(\mathrm{2}{x}+\mathrm{2}{y}+\mathrm{2}{z}−{l}\right)+\mathrm{2}\left({l}−\mathrm{2}{x}\right)}{\mathrm{2}{f}}=\frac{\mathrm{2}\left({l}−\mathrm{2}{x}−{y}−{z}\right)}{{f}}=\mathrm{0} \\ $$$$\Rightarrow{l}=\mathrm{2}{x}+{y}+{z} \\ $$$${similarly} \\ $$$$\Rightarrow{l}=\mathrm{2}{y}+{x}+{z} \\ $$$$\Rightarrow{l}=\mathrm{2}{z}+{y}+{x} \\ $$$$\Rightarrow\mathrm{3}{l}=\mathrm{4}\left({x}+{y}+{z}\right) \\ $$$$\Rightarrow{x}+{y}+{z}=\frac{\mathrm{3}{l}}{\mathrm{4}} \\ $$$$\Rightarrow{l}=\mathrm{2}{x}+{y}+{z}={x}+\frac{\mathrm{3}{l}}{\mathrm{4}} \\ $$$$\Rightarrow{x}=\frac{{l}}{\mathrm{4}} \\ $$$${similarly} \\ $$$$\Rightarrow{y}=\frac{{l}}{\mathrm{4}} \\ $$$$\Rightarrow{z}=\frac{{l}}{\mathrm{4}} \\ $$$$\Rightarrow{area}\:{is}\:{maximal}\:{if}\:{it}'{s}\:{a}\:{square}. \\ $$$${A}_{{max}} =\frac{{l}^{\mathrm{2}} }{\mathrm{16}} \\ $$
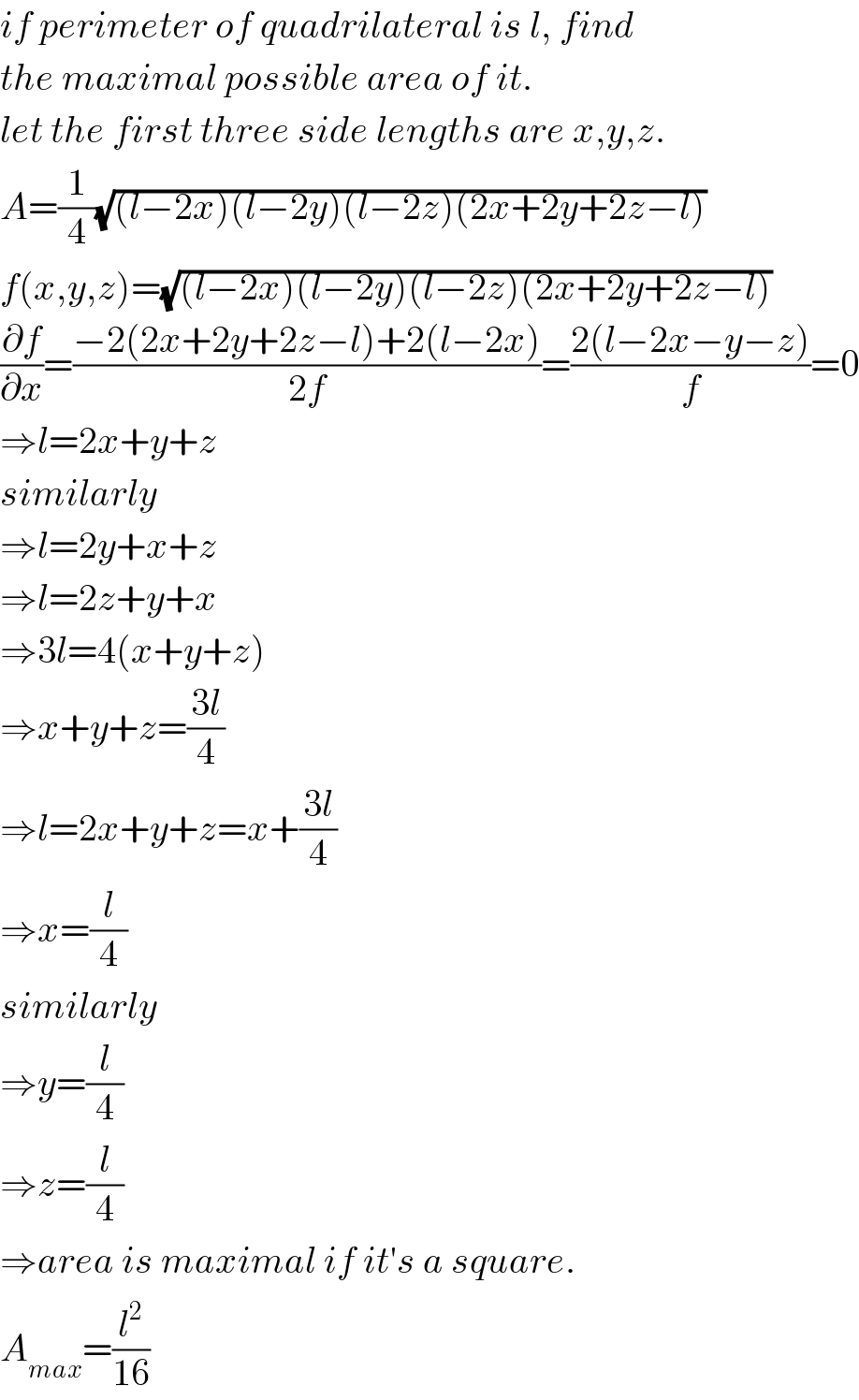
Commented by ajfour last updated on 19/Feb/18
$${Good}\:{way}\:{to}\:{verify}\:{Sir}! \\ $$