
Question and Answers Forum
Question Number 30259 by mondodotto@gmail.com last updated on 19/Feb/18

Commented by prof Abdo imad last updated on 20/Feb/18
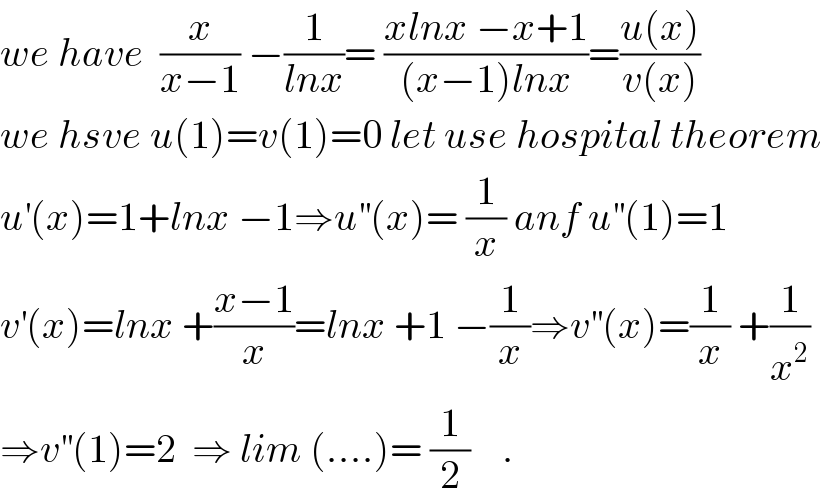
Answered by $@ty@m last updated on 19/Feb/18
![We have ln x=ln {1+(x−1)} =(x−1)−(((x−1)^2 )/2)+... ∴lim_(x→1) ((x/(x−1))−(1/(ln x))) ∴lim_(x→1) ((x/(x−1))−(1/((x−1)−(((x−1)^2 )/2)+(((x−1)^3 )/3)−...))) lim_(x→1) (1/(x−1)){x−(1/(1−((x−1)/2)+(((x−1)^2 )/3)−..))} lim_(x→1) (1/(x−1))[((x{1−((x−1)/2)+(((x−1)^2 )/3)−..}−1)/(1−((x−1)/2)+(((x−1)^2 )/3)−..))] lim_(x→1) (1/(x−1))[(((x−1)−((x(x−1))/2)+((x(x−1)^2 )/3)−..)/(1−((x−1)/2)+(((x−1)^2 )/3)−..))] lim_(x→1) ((x−1)/(x−1))[((1−(x/2)+((x(x−1))/3)−..)/(1−((x−1)/2)+(((x−1)^2 )/3)−..))] =(1/2)](Q30296.png)
| ||
Question and Answers Forum | ||
Question Number 30259 by mondodotto@gmail.com last updated on 19/Feb/18 | ||
 | ||
Commented by prof Abdo imad last updated on 20/Feb/18 | ||
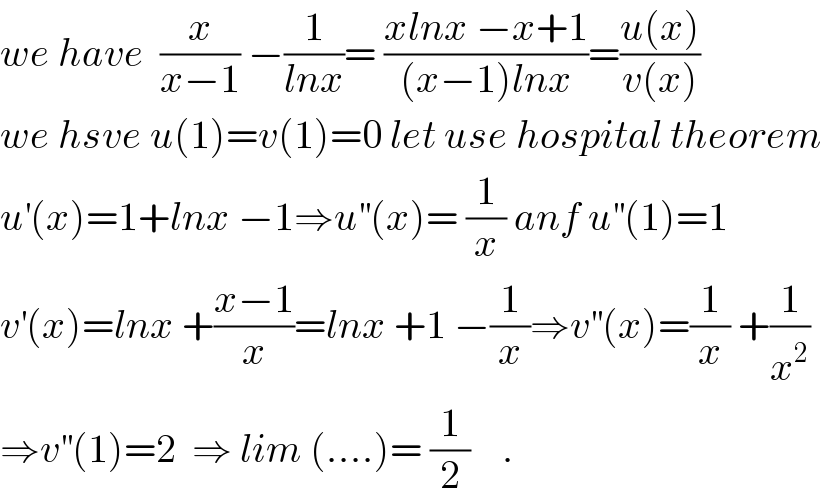 | ||
Answered by $@ty@m last updated on 19/Feb/18 | ||
![We have ln x=ln {1+(x−1)} =(x−1)−(((x−1)^2 )/2)+... ∴lim_(x→1) ((x/(x−1))−(1/(ln x))) ∴lim_(x→1) ((x/(x−1))−(1/((x−1)−(((x−1)^2 )/2)+(((x−1)^3 )/3)−...))) lim_(x→1) (1/(x−1)){x−(1/(1−((x−1)/2)+(((x−1)^2 )/3)−..))} lim_(x→1) (1/(x−1))[((x{1−((x−1)/2)+(((x−1)^2 )/3)−..}−1)/(1−((x−1)/2)+(((x−1)^2 )/3)−..))] lim_(x→1) (1/(x−1))[(((x−1)−((x(x−1))/2)+((x(x−1)^2 )/3)−..)/(1−((x−1)/2)+(((x−1)^2 )/3)−..))] lim_(x→1) ((x−1)/(x−1))[((1−(x/2)+((x(x−1))/3)−..)/(1−((x−1)/2)+(((x−1)^2 )/3)−..))] =(1/2)](Q30296.png) | ||
| ||