
Question and Answers Forum
Question Number 30364 by ajfour last updated on 21/Feb/18

Commented by ajfour last updated on 21/Feb/18

Commented by ajfour last updated on 21/Feb/18

Answered by mrW2 last updated on 22/Feb/18

Commented by mrW2 last updated on 23/Feb/18
![Eqn. of parabola in u−v−system: v=cu^2 with c=(1/(4a)) At point T(u,v): tan φ=(dv/du)=2cu ⇒u=((tan φ)/(2c))=2a tan φ=GT ⇒v=((tan^2 φ)/(4c))=a tan^2 φ=GV Length of parabola VT^(⌢) =l l=∫_0 ^( u) (√(1+((dv/du))^2 )) du=2a∫_0 ^( φ) (√(1+tan^2 φ)) d(tan φ) =a[tan φ (√(1+tan^2 φ))+ln (tan φ+(√(1+tan^2 φ)))] ST^(⌢) =VT^(⌢) =l rθ=a[tan φ (√(1+tan^2 φ))+ln (tan φ+(√(1+tan^2 φ)))] ⇒θ=(a/r)[tan φ (√(1+tan^2 φ))+ln (tan φ+(√(1+tan^2 φ)))] FG=GV−FV=v−a=a(tan^2 φ−1) Point F(x,y) in x−y−system: x=r sin θ+2a tan φ cos (π−φ−θ)−a(tan^2 φ−1) sin (π−φ−θ) ⇒x=r sin θ−2a tan φ cos (φ+θ)−a(tan^2 φ−1) sin (φ+θ) ⇒x(φ)=r sin {(a/r)[tan φ (√(1+tan^2 φ))+ln (tan φ+(√(1+tan^2 φ)))]}−2a tan φ cos {φ+(a/r)[tan φ (√(1+tan^2 φ))+ln (tan φ+(√(1+tan^2 φ)))]}−a(tan^2 φ−1) sin {φ+(a/r)[tan φ (√(1+tan^2 φ))+ln (tan φ+(√(1+tan^2 φ)))]} y=r cos θ+2a tan φ sin (π−φ−θ)+a(tan^2 φ−1) cos (π−φ−θ) y=r cos θ+2a tan φ sin (φ+θ)−a(tan^2 φ−1) cos (φ+θ) ⇒y(φ)=r cos {(a/r)[tan φ (√(1+tan^2 φ))+ln (tan φ+(√(1+tan^2 φ)))]}+2a tan φ sin {φ+(a/r)[tan φ (√(1+tan^2 φ))+ln (tan φ+(√(1+tan^2 φ)))]}−a(tan^2 φ−1) cos {φ+(a/r)[tan φ (√(1+tan^2 φ))+ln (tan φ+(√(1+tan^2 φ)))]} locus of focus F is: x(φ)=r sin {(a/r)[tan φ (√(1+tan^2 φ))+ln (tan φ+(√(1+tan^2 φ)))]}−2a tan φ cos {φ+(a/r)[tan φ (√(1+tan^2 φ))+ln (tan φ+(√(1+tan^2 φ)))]}−a(tan^2 φ−1) sin {φ+(a/r)[tan φ (√(1+tan^2 φ))+ln (tan φ+(√(1+tan^2 φ)))]} y(φ)=r cos {(a/r)[tan φ (√(1+tan^2 φ))+ln (tan φ+(√(1+tan^2 φ)))]}+2a tan φ sin {φ+(a/r)[tan φ (√(1+tan^2 φ))+ln (tan φ+(√(1+tan^2 φ)))]}−a(tan^2 φ−1) cos {φ+(a/r)[tan φ (√(1+tan^2 φ))+ln (tan φ+(√(1+tan^2 φ)))]} with −(π/2)<φ<(π/2)](Q30503.png)
Commented by ajfour last updated on 23/Feb/18

Commented by ajfour last updated on 23/Feb/18
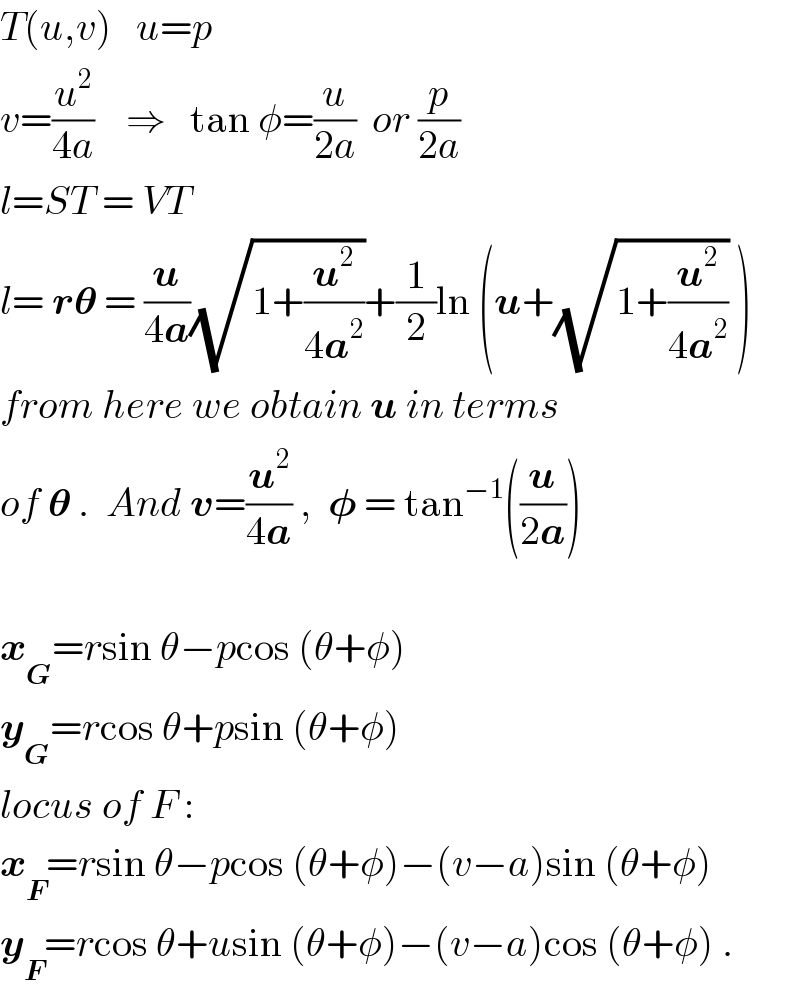
Commented by mrW2 last updated on 23/Feb/18

Commented by mrW2 last updated on 23/Feb/18

Commented by mrW2 last updated on 23/Feb/18

Commented by mrW2 last updated on 23/Feb/18
Commented by ajfour last updated on 23/Feb/18

