
Question and Answers Forum
Question Number 30522 by abdo imad last updated on 22/Feb/18
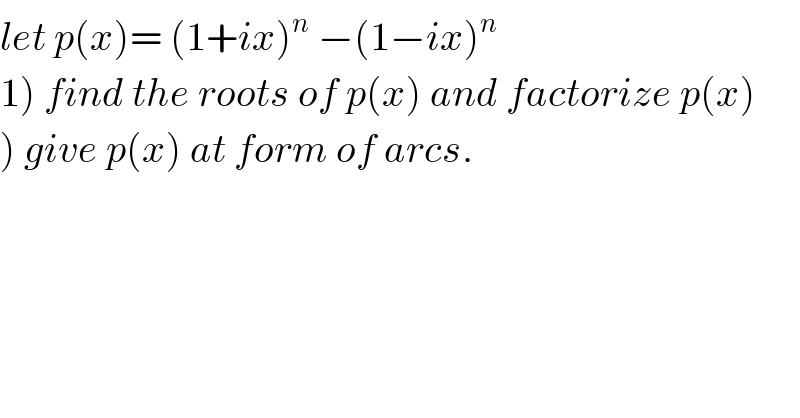
Commented by abdo imad last updated on 24/Feb/18
![1) we have p(x)=2i Im(1+ix)^n but ∣1+ix∣=(√(1+x^2 )) ⇒1+ix =(√(1+x^2 )) ( (1/(√(1+x^2 ))) +i (x/(√(1+x^2 ))))=r e^(iθ) ⇒r=(√(1+x^2 )) and cosθ =(1/(√(1+x^2 ))) and sinθ = (x/(√(1+x^2 ))) ⇒tanθ=x ⇒θ= artanx ⇒(1+ix)^n =((√(1+x^2 )))^n e^(inarctanx) ⇒ p(x)= 2i((√(1+x^2 )) )^n sin(narctanx) p(x)=0 ⇔ narctanx=kπ ⇔arctanx=((kπ)/n) ⇔ x_k =tan(((kπ)/n)) and k∈[[0,n−1]] and p(x)=λ Π_(k=0) ^(n−1) (x−tan(((kπ)/n)))let find λ we have p(x)= Σ_(k=0) ^n C_n ^k (ix)^k −Σ_(k=0) ^n C_n ^k (−ix)^k =Σ_(k=0) ^n C_n ^k ((i)^k −(−i)^k )x^k =2i Σ_(p=0) ^([((n−1)/2)]) C_n ^(2p+1) x^(2p+1) ⇒λ= 2i C_n ^(2[((n−1)/2)]+1) ⇒ p(x)= 2i C_n ^(2[((n−1)/2)]+1) Π_(k=0) ^(n−1) (x−tan(((kπ)/n))) . 2) p(x)=2i ((√(1+x^2 )) )^n sin(narctanx).](Q30699.png)
Answered by sma3l2996 last updated on 23/Feb/18
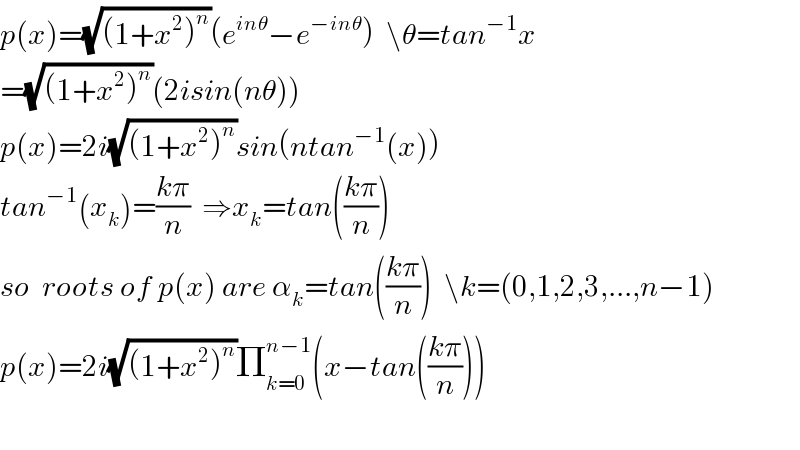
Commented by abdo imad last updated on 24/Feb/18

| ||
Question and Answers Forum | ||
Question Number 30522 by abdo imad last updated on 22/Feb/18 | ||
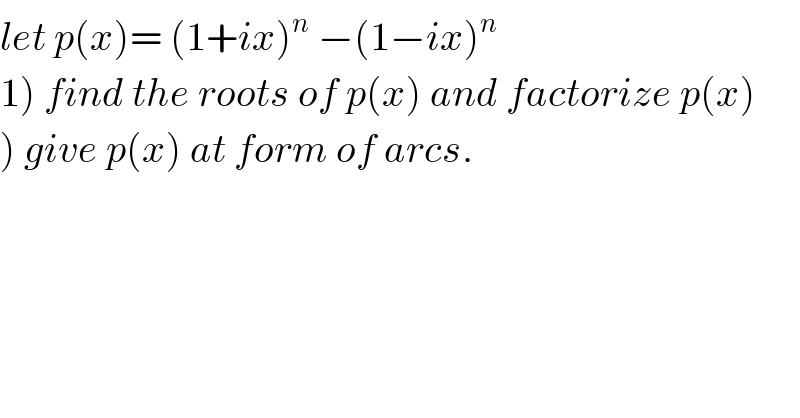 | ||
Commented by abdo imad last updated on 24/Feb/18 | ||
![1) we have p(x)=2i Im(1+ix)^n but ∣1+ix∣=(√(1+x^2 )) ⇒1+ix =(√(1+x^2 )) ( (1/(√(1+x^2 ))) +i (x/(√(1+x^2 ))))=r e^(iθ) ⇒r=(√(1+x^2 )) and cosθ =(1/(√(1+x^2 ))) and sinθ = (x/(√(1+x^2 ))) ⇒tanθ=x ⇒θ= artanx ⇒(1+ix)^n =((√(1+x^2 )))^n e^(inarctanx) ⇒ p(x)= 2i((√(1+x^2 )) )^n sin(narctanx) p(x)=0 ⇔ narctanx=kπ ⇔arctanx=((kπ)/n) ⇔ x_k =tan(((kπ)/n)) and k∈[[0,n−1]] and p(x)=λ Π_(k=0) ^(n−1) (x−tan(((kπ)/n)))let find λ we have p(x)= Σ_(k=0) ^n C_n ^k (ix)^k −Σ_(k=0) ^n C_n ^k (−ix)^k =Σ_(k=0) ^n C_n ^k ((i)^k −(−i)^k )x^k =2i Σ_(p=0) ^([((n−1)/2)]) C_n ^(2p+1) x^(2p+1) ⇒λ= 2i C_n ^(2[((n−1)/2)]+1) ⇒ p(x)= 2i C_n ^(2[((n−1)/2)]+1) Π_(k=0) ^(n−1) (x−tan(((kπ)/n))) . 2) p(x)=2i ((√(1+x^2 )) )^n sin(narctanx).](Q30699.png) | ||
Answered by sma3l2996 last updated on 23/Feb/18 | ||
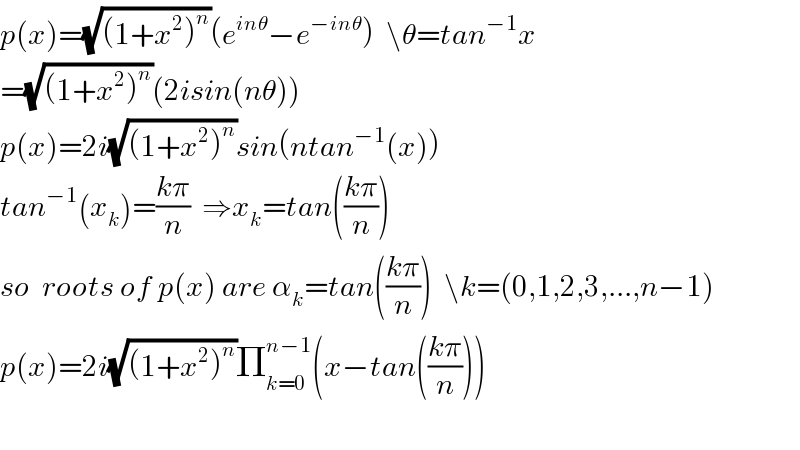 | ||
| ||
Commented by abdo imad last updated on 24/Feb/18 | ||
 | ||