
Question and Answers Forum
Question Number 30527 by abdo imad last updated on 22/Feb/18
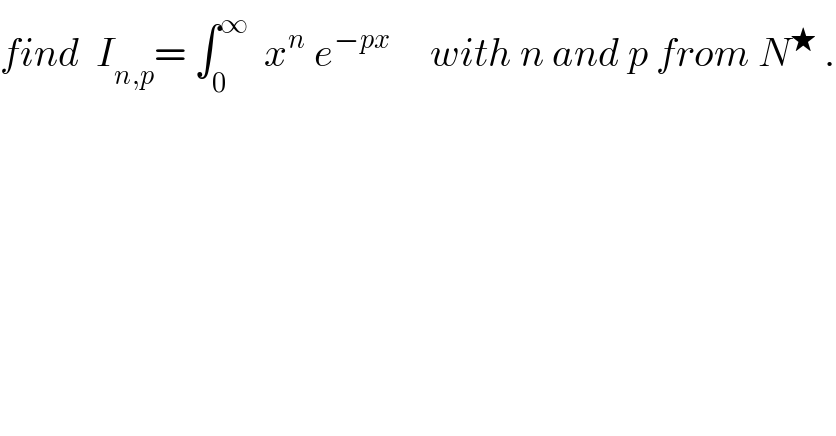
Answered by sma3l2996 last updated on 23/Feb/18
![I=∫_0 ^∞ x^n e^(−px) dx u=x^n ⇒u′=nx^(n−1) v′=e^(−px) ⇒v=((−1)/p)e^(−px) I=−(1/p)[x^n e^(−px) ]_0 ^∞ +(n/p)∫_0 ^∞ x^(n−1) e^(−px) dx (lim_(x→∞) x^n e^(−px) =0) =(n/p)∫_0 ^∞ x^(n−1) e^(−px) dx u=x^(n−1) ⇒u′=(n−1)x^(n−2) v′=e^(−px) ⇒v=((−1)/p)e^(−px) I=((n(n−1))/p^2 )∫_0 ^∞ x^(n−2) e^(−px) dx . . . k times I=((n(n−1)(n−2)...(n−k+1))/p^k )∫_0 ^∞ x^(n−k) e^(−px) dx . . . n times I=((n(n−1)(n−2)...(n−n+1))/p^n )∫_0 ^∞ e^(−px) dx I=((n!)/p^n )[−(1/p)e^(−px) ]_0 ^∞ =((n!)/p^(n+1) )(−(lim_(x→∞) e^(−px) −e^0 )) I=((n!)/p^(n+1) )](Q30531.png)
| ||
Question and Answers Forum | ||
Question Number 30527 by abdo imad last updated on 22/Feb/18 | ||
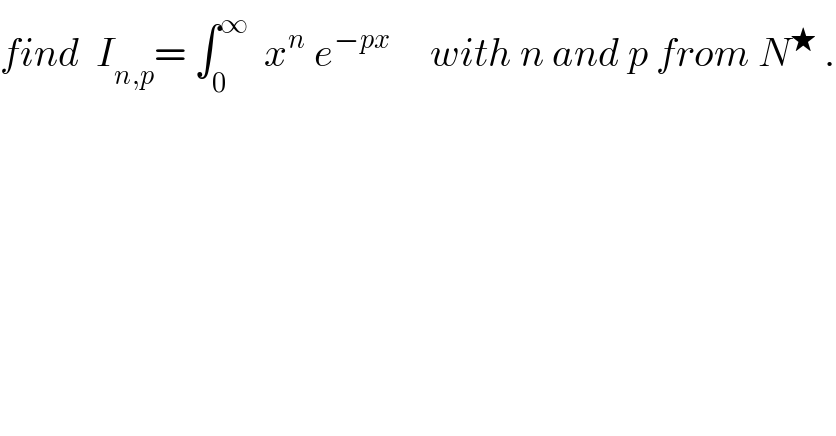 | ||
Answered by sma3l2996 last updated on 23/Feb/18 | ||
![I=∫_0 ^∞ x^n e^(−px) dx u=x^n ⇒u′=nx^(n−1) v′=e^(−px) ⇒v=((−1)/p)e^(−px) I=−(1/p)[x^n e^(−px) ]_0 ^∞ +(n/p)∫_0 ^∞ x^(n−1) e^(−px) dx (lim_(x→∞) x^n e^(−px) =0) =(n/p)∫_0 ^∞ x^(n−1) e^(−px) dx u=x^(n−1) ⇒u′=(n−1)x^(n−2) v′=e^(−px) ⇒v=((−1)/p)e^(−px) I=((n(n−1))/p^2 )∫_0 ^∞ x^(n−2) e^(−px) dx . . . k times I=((n(n−1)(n−2)...(n−k+1))/p^k )∫_0 ^∞ x^(n−k) e^(−px) dx . . . n times I=((n(n−1)(n−2)...(n−n+1))/p^n )∫_0 ^∞ e^(−px) dx I=((n!)/p^n )[−(1/p)e^(−px) ]_0 ^∞ =((n!)/p^(n+1) )(−(lim_(x→∞) e^(−px) −e^0 )) I=((n!)/p^(n+1) )](Q30531.png) | ||
| ||