Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 30590 by abdo imad last updated on 23/Feb/18

decompose sur R[x] x^(2n+1) −1.

$${decompose}\:{sur}\:{R}\left[{x}\right]\:\:{x}^{\mathrm{2}{n}+\mathrm{1}} \:−\mathrm{1}. \\ $$

Answered by sma3l2996 last updated on 23/Feb/18

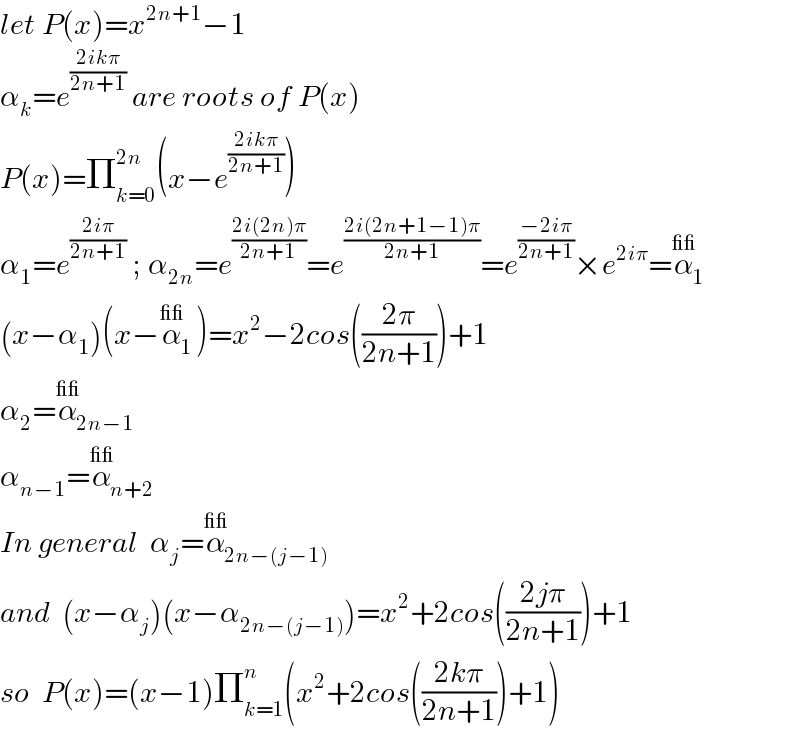
let P(x)=x^(2n+1) −1 α_k =e^((2ikπ)/(2n+1)) are roots of P(x) P(x)=Π_(k=0) ^(2n) (x−e^((2ikπ)/(2n+1)) ) α_1 =e^((2iπ)/(2n+1)) ; α_(2n) =e^((2i(2n)π)/(2n+1)) =e^((2i(2n+1−1)π)/(2n+1)) =e^((−2iπ)/(2n+1)) ×e^(2iπ) =α_1 ^(__) (x−α_1 )(x−α_1 ^(__) )=x^2 −2cos(((2π)/(2n+1)))+1 α_2 =α_(2n−1) ^(__) α_(n−1) =α_(n+2) ^(__) In general α_j =α_(2n−(j−1)) ^(__) and (x−α_j )(x−α_(2n−(j−1)) )=x^2 +2cos(((2jπ)/(2n+1)))+1 so P(x)=(x−1)Π_(k=1) ^n (x^2 +2cos(((2kπ)/(2n+1)))+1)

$${let}\:{P}\left({x}\right)={x}^{\mathrm{2}{n}+\mathrm{1}} −\mathrm{1} \\ $$$$\alpha_{{k}} ={e}^{\frac{\mathrm{2}{ik}\pi}{\mathrm{2}{n}+\mathrm{1}}} \:{are}\:{roots}\:{of}\:{P}\left({x}\right) \\ $$$${P}\left({x}\right)=\prod_{{k}=\mathrm{0}} ^{\mathrm{2}{n}} \left({x}−{e}^{\frac{\mathrm{2}{ik}\pi}{\mathrm{2}{n}+\mathrm{1}}} \right) \\ $$$$\alpha_{\mathrm{1}} ={e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{2}{n}+\mathrm{1}}} \:;\:\alpha_{\mathrm{2}{n}} ={e}^{\frac{\mathrm{2}{i}\left(\mathrm{2}{n}\right)\pi}{\mathrm{2}{n}+\mathrm{1}}} ={e}^{\frac{\mathrm{2}{i}\left(\mathrm{2}{n}+\mathrm{1}−\mathrm{1}\right)\pi}{\mathrm{2}{n}+\mathrm{1}}} ={e}^{\frac{−\mathrm{2}{i}\pi}{\mathrm{2}{n}+\mathrm{1}}} ×{e}^{\mathrm{2}{i}\pi} =\overset{\_\_} {\alpha}_{\mathrm{1}} \\ $$$$\left({x}−\alpha_{\mathrm{1}} \right)\left({x}−\overset{\_\_} {\alpha}_{\mathrm{1}} \right)={x}^{\mathrm{2}} −\mathrm{2}{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)+\mathrm{1} \\ $$$$\alpha_{\mathrm{2}} =\overset{\_\_} {\alpha}_{\mathrm{2}{n}−\mathrm{1}} \\ $$$$\alpha_{{n}−\mathrm{1}} =\overset{\_\_} {\alpha}_{{n}+\mathrm{2}} \\ $$$${In}\:{general}\:\:\alpha_{{j}} =\overset{\_\_} {\alpha}_{\mathrm{2}{n}−\left({j}−\mathrm{1}\right)} \\ $$$${and}\:\:\left({x}−\alpha_{{j}} \right)\left({x}−\alpha_{\mathrm{2}{n}−\left({j}−\mathrm{1}\right)} \right)={x}^{\mathrm{2}} +\mathrm{2}{cos}\left(\frac{\mathrm{2}{j}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)+\mathrm{1} \\ $$$${so}\:\:{P}\left({x}\right)=\left({x}−\mathrm{1}\right)\prod_{{k}=\mathrm{1}} ^{{n}} \left({x}^{\mathrm{2}} +\mathrm{2}{cos}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)+\mathrm{1}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com