Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 30592 by abdo imad last updated on 23/Feb/18

let p(x)=x^(2n) −2cosα x^n +1 1) find roots lf p(x) 2)factorize p(x) inside C[x] 3)factorize p(x) inside R[x].

$${let}\:{p}\left({x}\right)={x}^{\mathrm{2}{n}} \:−\mathrm{2}{cos}\alpha\:{x}^{{n}} \:+\mathrm{1} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{roots}\:{lf}\:{p}\left({x}\right) \\ $$$$\left.\mathrm{2}\right){factorize}\:{p}\left({x}\right)\:{inside}\:{C}\left[{x}\right] \\ $$$$\left.\mathrm{3}\right){factorize}\:{p}\left({x}\right)\:{inside}\:{R}\left[{x}\right]. \\ $$

Answered by sma3l2996 last updated on 23/Feb/18

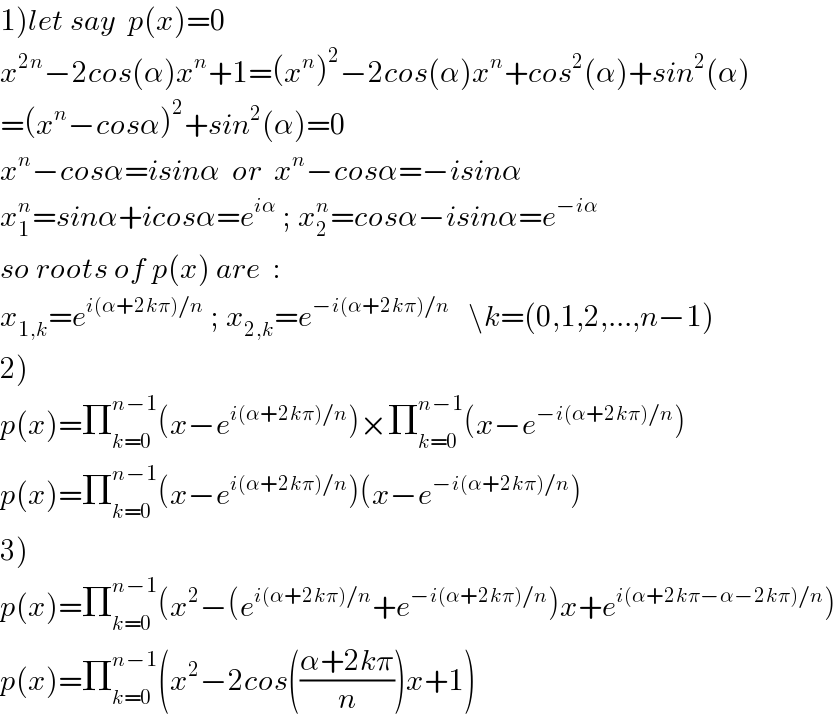
1)let say p(x)=0 x^(2n) −2cos(α)x^n +1=(x^n )^2 −2cos(α)x^n +cos^2 (α)+sin^2 (α) =(x^n −cosα)^2 +sin^2 (α)=0 x^n −cosα=isinα or x^n −cosα=−isinα x_1 ^n =sinα+icosα=e^(iα) ; x_2 ^n =cosα−isinα=e^(−iα) so roots of p(x) are : x_(1,k) =e^(i(α+2kπ)/n) ; x_(2,k) =e^(−i(α+2kπ)/n) \k=(0,1,2,...,n−1) 2) p(x)=Π_(k=0) ^(n−1) (x−e^(i(α+2kπ)/n) )×Π_(k=0) ^(n−1) (x−e^(−i(α+2kπ)/n) ) p(x)=Π_(k=0) ^(n−1) (x−e^(i(α+2kπ)/n) )(x−e^(−i(α+2kπ)/n) ) 3) p(x)=Π_(k=0) ^(n−1) (x^2 −(e^(i(α+2kπ)/n) +e^(−i(α+2kπ)/n) )x+e^(i(α+2kπ−α−2kπ)/n) ) p(x)=Π_(k=0) ^(n−1) (x^2 −2cos(((α+2kπ)/n))x+1)

$$\left.\mathrm{1}\right){let}\:{say}\:\:{p}\left({x}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}{n}} −\mathrm{2}{cos}\left(\alpha\right){x}^{{n}} +\mathrm{1}=\left({x}^{{n}} \right)^{\mathrm{2}} −\mathrm{2}{cos}\left(\alpha\right){x}^{{n}} +{cos}^{\mathrm{2}} \left(\alpha\right)+{sin}^{\mathrm{2}} \left(\alpha\right) \\ $$$$=\left({x}^{{n}} −{cos}\alpha\right)^{\mathrm{2}} +{sin}^{\mathrm{2}} \left(\alpha\right)=\mathrm{0} \\ $$$${x}^{{n}} −{cos}\alpha={isin}\alpha\:\:{or}\:\:{x}^{{n}} −{cos}\alpha=−{isin}\alpha \\ $$$${x}_{\mathrm{1}} ^{{n}} ={sin}\alpha+{icos}\alpha={e}^{{i}\alpha} \:;\:{x}_{\mathrm{2}} ^{{n}} ={cos}\alpha−{isin}\alpha={e}^{−{i}\alpha} \\ $$$${so}\:{roots}\:{of}\:{p}\left({x}\right)\:{are}\:\:: \\ $$$${x}_{\mathrm{1},{k}} ={e}^{{i}\left(\alpha+\mathrm{2}{k}\pi\right)/{n}} \:;\:{x}_{\mathrm{2},{k}} ={e}^{−{i}\left(\alpha+\mathrm{2}{k}\pi\right)/{n}} \:\:\:\backslash{k}=\left(\mathrm{0},\mathrm{1},\mathrm{2},...,{n}−\mathrm{1}\right) \\ $$$$\left.\mathrm{2}\right) \\ $$$${p}\left({x}\right)=\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}−{e}^{{i}\left(\alpha+\mathrm{2}{k}\pi\right)/{n}} \right)×\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}−{e}^{−{i}\left(\alpha+\mathrm{2}{k}\pi\right)/{n}} \right) \\ $$$${p}\left({x}\right)=\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}−{e}^{{i}\left(\alpha+\mathrm{2}{k}\pi\right)/{n}} \right)\left({x}−{e}^{−{i}\left(\alpha+\mathrm{2}{k}\pi\right)/{n}} \right) \\ $$$$\left.\mathrm{3}\right) \\ $$$${p}\left({x}\right)=\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}^{\mathrm{2}} −\left({e}^{{i}\left(\alpha+\mathrm{2}{k}\pi\right)/{n}} +{e}^{−{i}\left(\alpha+\mathrm{2}{k}\pi\right)/{n}} \right){x}+{e}^{{i}\left(\alpha+\mathrm{2}{k}\pi−\alpha−\mathrm{2}{k}\pi\right)/{n}} \right) \\ $$$${p}\left({x}\right)=\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}^{\mathrm{2}} −\mathrm{2}{cos}\left(\frac{\alpha+\mathrm{2}{k}\pi}{{n}}\right){x}+\mathrm{1}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com