
Question and Answers Forum
Question Number 30599 by abdo imad last updated on 23/Feb/18
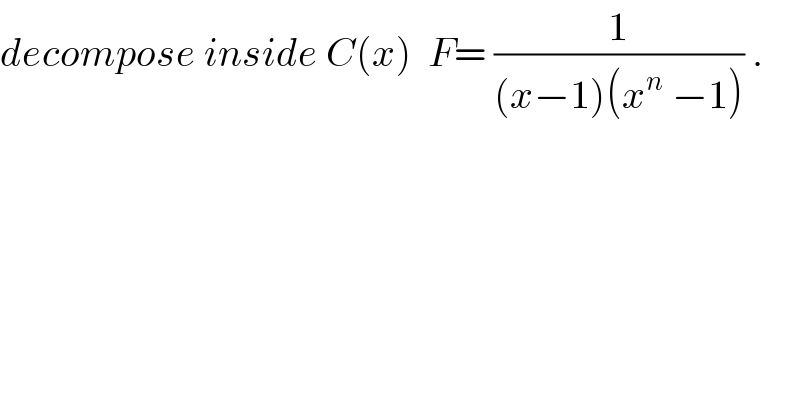
Commented by abdo imad last updated on 25/Feb/18
![the roots of z^n −1=0 are the complex z_k = e^(i((2kπ)/k)) with k∈[[0,n−1]] ⇒F will be decomposed inside C(x) at form F(x)= (a/(x−1)) +(b/((x−1)^2 )) +Σ_(k=1) ^(n−1) (λ_k /(x−z_k )) we have (x−1)(x^n −1)=x^(n+1) −x −x^n +1 ⇒ (d/dx)( (x−1)(x^n −1))=(n+1)x^n −nx^(n−1) −1⇒ λ_k = (1/((n+1)z_k ^n −n z_k ^(n−1) −1)) =(1/(n+1−(n/z_k )−1))= (z_k /(nz_k −n)) the ch.x−1=y give F(x)= (1/((x−1)^2 (1+x +x^2 +...+x^(n−1) ))) =g(y)= (1/(y^2 (1+(1+y) +(1+y)^2 +....(1+y)^(n−1) ))) after divide 1 per 2+y +(1+y)^2 +...(1+y)^(n−1) folowing the increasing powers after all calculus we find a=((1−n)/(2n)) and b= (1/n) look also that b=lim_(x→1) (x−1)^2 F(x)=lim_(x→1) (1/(1+x +x^2 +...+x^(n−1) )) =(1/n)](Q30791.png)
| ||
Question and Answers Forum | ||
Question Number 30599 by abdo imad last updated on 23/Feb/18 | ||
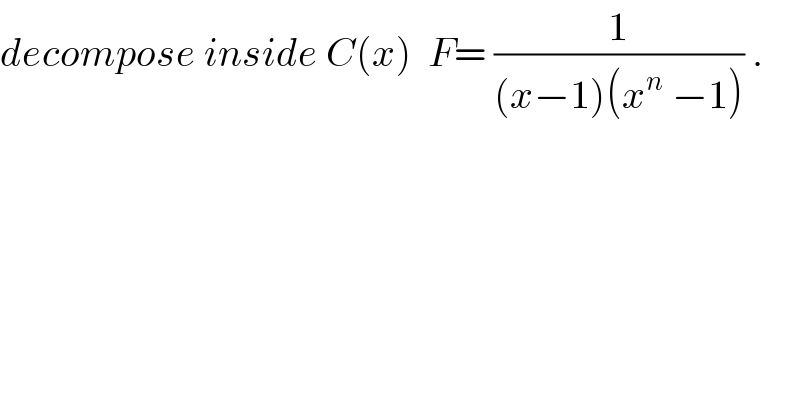 | ||
Commented by abdo imad last updated on 25/Feb/18 | ||
![the roots of z^n −1=0 are the complex z_k = e^(i((2kπ)/k)) with k∈[[0,n−1]] ⇒F will be decomposed inside C(x) at form F(x)= (a/(x−1)) +(b/((x−1)^2 )) +Σ_(k=1) ^(n−1) (λ_k /(x−z_k )) we have (x−1)(x^n −1)=x^(n+1) −x −x^n +1 ⇒ (d/dx)( (x−1)(x^n −1))=(n+1)x^n −nx^(n−1) −1⇒ λ_k = (1/((n+1)z_k ^n −n z_k ^(n−1) −1)) =(1/(n+1−(n/z_k )−1))= (z_k /(nz_k −n)) the ch.x−1=y give F(x)= (1/((x−1)^2 (1+x +x^2 +...+x^(n−1) ))) =g(y)= (1/(y^2 (1+(1+y) +(1+y)^2 +....(1+y)^(n−1) ))) after divide 1 per 2+y +(1+y)^2 +...(1+y)^(n−1) folowing the increasing powers after all calculus we find a=((1−n)/(2n)) and b= (1/n) look also that b=lim_(x→1) (x−1)^2 F(x)=lim_(x→1) (1/(1+x +x^2 +...+x^(n−1) )) =(1/n)](Q30791.png) | ||