Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 3062 by 123456 last updated on 04/Dec/15

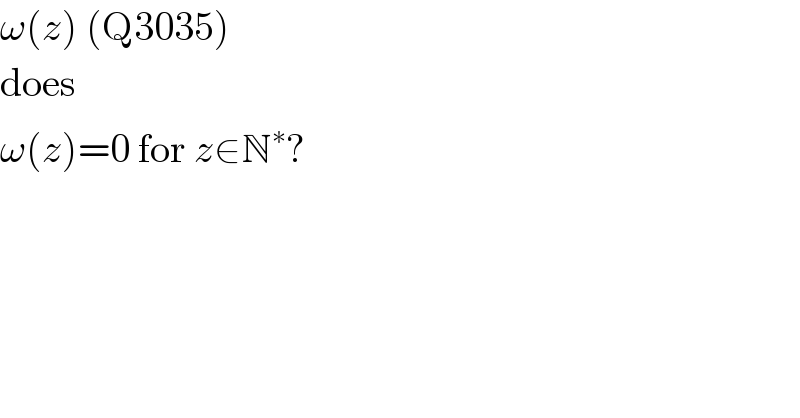
ω(z) (Q3035) does ω(z)=0 for z∈N^∗ ?

$$\omega\left({z}\right)\:\left(\mathrm{Q3035}\right) \\ $$$$\mathrm{does} \\ $$$$\omega\left({z}\right)=\mathrm{0}\:\mathrm{for}\:{z}\in\mathbb{N}^{\ast} ? \\ $$

Commented by Filup last updated on 04/Dec/15

What is N^∗ ?

$$\mathrm{What}\:\mathrm{is}\:\mathbb{N}^{\ast} ? \\ $$

Commented by Filup last updated on 04/Dec/15

ω(z)=lim_(n→∞) ((n^z [z+(z+1)+...+(z+n)])/(z(z+1)∙∙∙(z+n)))

$$\omega\left({z}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}^{{z}} \left[{z}+\left({z}+\mathrm{1}\right)+...+\left({z}+{n}\right)\right]}{{z}\left({z}+\mathrm{1}\right)\centerdot\centerdot\centerdot\left({z}+{n}\right)} \\ $$

Commented by 123456 last updated on 04/Dec/15

N^∗ =N/{0}

$$\mathbb{N}^{\ast} =\mathbb{N}/\left\{\mathrm{0}\right\} \\ $$

Commented by Filup last updated on 04/Dec/15

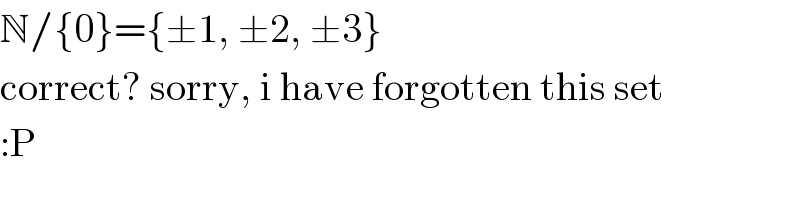
N/{0}={±1, ±2, ±3} correct? sorry, i have forgotten this set :P

$$\mathbb{N}/\left\{\mathrm{0}\right\}=\left\{\pm\mathrm{1},\:\pm\mathrm{2},\:\pm\mathrm{3}\right\} \\ $$$$\mathrm{correct}?\:\mathrm{sorry},\:\mathrm{i}\:\mathrm{have}\:\mathrm{forgotten}\:\mathrm{this}\:\mathrm{set} \\ $$$$:\mathrm{P} \\ $$

Commented by 123456 last updated on 04/Dec/15

N={0,1,2,...} (natural numbers) the set you shown is Z={0,±1,±2,...} (integer numbers) Z^∗ =Z/{0}={±1,±2,...}

$$\mathbb{N}=\left\{\mathrm{0},\mathrm{1},\mathrm{2},...\right\}\:\left(\mathrm{natural}\:\mathrm{numbers}\right) \\ $$$$\mathrm{the}\:\mathrm{set}\:\mathrm{you}\:\mathrm{shown}\:\mathrm{is} \\ $$$$\mathbb{Z}=\left\{\mathrm{0},\pm\mathrm{1},\pm\mathrm{2},...\right\}\:\left(\mathrm{integer}\:\mathrm{numbers}\right) \\ $$$$\mathbb{Z}^{\ast} =\mathbb{Z}/\left\{\mathrm{0}\right\}=\left\{\pm\mathrm{1},\pm\mathrm{2},...\right\} \\ $$

Commented by Filup last updated on 04/Dec/15

Ah! Thanks!!!

$${Ah}!\:\mathrm{T}{hanks}!!! \\ $$

Commented by prakash jain last updated on 04/Dec/15

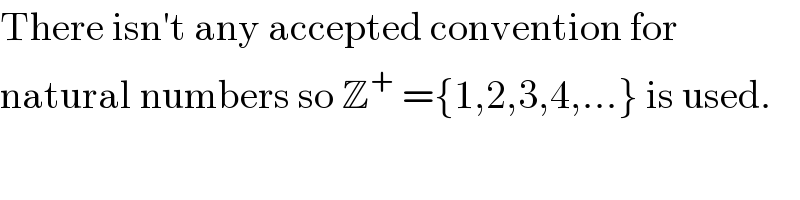
There isn′t any accepted convention for natural numbers so Z^+ ={1,2,3,4,...} is used.

$$\mathrm{There}\:\mathrm{isn}'\mathrm{t}\:\mathrm{any}\:\mathrm{accepted}\:\mathrm{convention}\:\mathrm{for}\: \\ $$$$\mathrm{natural}\:\mathrm{numbers}\:\mathrm{so}\:\mathbb{Z}^{+} \:=\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},...\right\}\:\mathrm{is}\:\mathrm{used}. \\ $$

Commented by 123456 last updated on 04/Dec/15

its have N={0,1,2,...} or N={1,2,3,...} its depends from people to people and source to source, the two have their advantagens

$$\mathrm{its}\:\mathrm{have} \\ $$$$\mathbb{N}=\left\{\mathrm{0},\mathrm{1},\mathrm{2},...\right\} \\ $$$$\mathrm{or} \\ $$$$\mathbb{N}=\left\{\mathrm{1},\mathrm{2},\mathrm{3},...\right\} \\ $$$$\mathrm{its}\:\mathrm{depends}\:\mathrm{from}\:\mathrm{people}\:\mathrm{to}\:\mathrm{people}\:\mathrm{and} \\ $$$$\mathrm{source}\:\mathrm{to}\:\mathrm{source},\:\mathrm{the}\:\mathrm{two}\:\mathrm{have}\:\mathrm{their} \\ $$$$\mathrm{advantagens} \\ $$$$ \\ $$

Answered by Filup last updated on 04/Dec/15

ω(z)=lim_(n→∞) ((n^z [z+(z+1)+...+(z+n)])/(z(z+1)∙∙∙(z+n))) ω(z)=lim_(n→∞) ((n^z (z+Σ_(i=1) ^n (z+i)))/(((z+n)!)/((z−1)!))) ω(z)=lim_(n→∞) ((n^z [z+(1/2)n(2z+n+1)])/(((z+n)!)/((z−1)!))) ω(z)=lim_(n→∞) ((n^z [z+(1/2)(2zn+n^2 +n)])/(((z+n)!)/((z−1)!))) ω(z)=lim_(n→∞) (([2zn^z +2zn^(z+1) +n^(z+2) +n^(z+1) ](z−1)!)/(2(z+n)!)) ω(z)=lim_(n→∞) (((2zn^z +2z(n^(z+1) +1)+n^(z+2) )(z−1)!)/(2(z+n)!)) ω(z)=lim_(n→∞) (((2z(n^z +n^(z+1) +1)+n^(z+2) )(z−1)!)/(2(z+n)!)) ω(z)=lim_(n→∞) ((2z(n^z +n^(z+1) +1)+n^(z+2) )/(2(z+n)!)) (z−1)! ω(z)=lim_(n→∞) (((z(n^z +n^(z+1) +1))/((z+n)!)) + (n^(z+2) /(2(z+n)!)))(z−1)! ω(z)=lim_(n→∞) (z−1)!∙(z[(n^z /((z+n)!))+(n^(z+1) /((z+n)!))+(1/((z+n)!))] + (n^(z+2) /(2(z+n)!))) continue (will edit if I figure it out)

$$\omega\left({z}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}^{{z}} \left[{z}+\left({z}+\mathrm{1}\right)+...+\left({z}+{n}\right)\right]}{{z}\left({z}+\mathrm{1}\right)\centerdot\centerdot\centerdot\left({z}+{n}\right)} \\ $$$$ \\ $$$$\omega\left({z}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}^{{z}} \left({z}+\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left({z}+{i}\right)\right)}{\frac{\left({z}+{n}\right)!}{\left({z}−\mathrm{1}\right)!}} \\ $$$$\omega\left({z}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}^{{z}} \left[{z}+\frac{\mathrm{1}}{\mathrm{2}}{n}\left(\mathrm{2}{z}+{n}+\mathrm{1}\right)\right]}{\frac{\left({z}+{n}\right)!}{\left({z}−\mathrm{1}\right)!}} \\ $$$$\omega\left({z}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}^{{z}} \left[{z}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{zn}+{n}^{\mathrm{2}} +{n}\right)\right]}{\frac{\left({z}+{n}\right)!}{\left({z}−\mathrm{1}\right)!}} \\ $$$$\omega\left({z}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\left[\mathrm{2}{zn}^{{z}} +\mathrm{2}{zn}^{{z}+\mathrm{1}} +{n}^{{z}+\mathrm{2}} +{n}^{{z}+\mathrm{1}} \right]\left({z}−\mathrm{1}\right)!}{\mathrm{2}\left({z}+{n}\right)!} \\ $$$$\omega\left({z}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{2}{zn}^{{z}} +\mathrm{2}{z}\left({n}^{{z}+\mathrm{1}} +\mathrm{1}\right)+{n}^{{z}+\mathrm{2}} \right)\left({z}−\mathrm{1}\right)!}{\mathrm{2}\left({z}+{n}\right)!} \\ $$$$\omega\left({z}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{2}{z}\left({n}^{{z}} +{n}^{{z}+\mathrm{1}} +\mathrm{1}\right)+{n}^{{z}+\mathrm{2}} \right)\left({z}−\mathrm{1}\right)!}{\mathrm{2}\left({z}+{n}\right)!} \\ $$$$\omega\left({z}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}{z}\left({n}^{{z}} +{n}^{{z}+\mathrm{1}} +\mathrm{1}\right)+{n}^{{z}+\mathrm{2}} }{\mathrm{2}\left({z}+{n}\right)!}\:\left({z}−\mathrm{1}\right)! \\ $$$$\omega\left({z}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{z}\left({n}^{{z}} +{n}^{{z}+\mathrm{1}} +\mathrm{1}\right)}{\left({z}+{n}\right)!}\:+\:\frac{{n}^{{z}+\mathrm{2}} }{\mathrm{2}\left({z}+{n}\right)!}\right)\left({z}−\mathrm{1}\right)! \\ $$$$\omega\left({z}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left({z}−\mathrm{1}\right)!\centerdot\left({z}\left[\frac{{n}^{{z}} }{\left({z}+{n}\right)!}+\frac{{n}^{{z}+\mathrm{1}} }{\left({z}+{n}\right)!}+\frac{\mathrm{1}}{\left({z}+{n}\right)!}\right]\:+\:\frac{{n}^{{z}+\mathrm{2}} }{\mathrm{2}\left({z}+{n}\right)!}\right) \\ $$$$ \\ $$$$\mathrm{continue}\:\:\left(\mathrm{will}\:\mathrm{edit}\:\mathrm{if}\:\mathrm{I}\:\mathrm{figure}\:\mathrm{it}\:\mathrm{out}\right) \\ $$

Answered by prakash jain last updated on 04/Dec/15

w_n (z)=((n^z [z+(z+1)+..+(z+n)])/(z(z+1)..(z+n))) =((n^z [((n+1)/2)(2z+n)])/(((z+n)!)/((z−1)!))) =((n^z (z−1)!(n+1)(2z+n))/(2(z+n)!)) =(((z−1)!)/2)∙((n^z (2nz+2z+n^2 ))/((n+z)!)) =k_1 ∙(n^(z+1) /((n+z)!))+k_2 ∙(n^z /((n+z)!))+k_3 ∙(n^(z+2) /((n+z)!)) lim_(n→∞) (n^(z+2) /((n+z)!))=lim_(n→∞) (n^(z+2) /((n+z)!))≤lim_(n→∞) (n^(z+2) /((n−1)!n^(z+1) )) =lim_(n→∞) (n/((n−1)!))=0 simlarly lim_(n→∞) (n^(z+1) /((n+z)!))=0 and lim_(n→∞) (n^z /((n+z)!))=0 lim_(n→∞) w_n (z)=w(z)=0

$${w}_{{n}} \left({z}\right)=\frac{{n}^{{z}} \left[{z}+\left({z}+\mathrm{1}\right)+..+\left({z}+{n}\right)\right]}{{z}\left({z}+\mathrm{1}\right)..\left({z}+{n}\right)} \\ $$$$=\frac{{n}^{{z}} \left[\frac{{n}+\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{z}+{n}\right)\right]}{\frac{\left({z}+{n}\right)!}{\left({z}−\mathrm{1}\right)!}} \\ $$$$=\frac{{n}^{{z}} \left({z}−\mathrm{1}\right)!\left({n}+\mathrm{1}\right)\left(\mathrm{2}{z}+{n}\right)}{\mathrm{2}\left({z}+{n}\right)!} \\ $$$$=\frac{\left({z}−\mathrm{1}\right)!}{\mathrm{2}}\centerdot\frac{{n}^{{z}} \left(\mathrm{2}{nz}+\mathrm{2}{z}+{n}^{\mathrm{2}} \right)}{\left({n}+{z}\right)!} \\ $$$$={k}_{\mathrm{1}} \centerdot\frac{{n}^{{z}+\mathrm{1}} }{\left({n}+{z}\right)!}+{k}_{\mathrm{2}} \centerdot\frac{{n}^{{z}} }{\left({n}+{z}\right)!}+{k}_{\mathrm{3}} \centerdot\frac{{n}^{{z}+\mathrm{2}} }{\left({n}+{z}\right)!} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}^{{z}+\mathrm{2}} }{\left({n}+{z}\right)!}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}^{{z}+\mathrm{2}} }{\left({n}+{z}\right)!}\leqslant\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}^{{z}+\mathrm{2}} }{\left({n}−\mathrm{1}\right)!{n}^{{z}+\mathrm{1}} } \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}}{\left({n}−\mathrm{1}\right)!}=\mathrm{0} \\ $$$$\mathrm{simlarly}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}^{{z}+\mathrm{1}} }{\left({n}+{z}\right)!}=\mathrm{0} \\ $$$$\mathrm{and}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}^{{z}} }{\left({n}+{z}\right)!}=\mathrm{0} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{w}_{{n}} \left({z}\right)={w}\left({z}\right)=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com