
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 30752 by abdo imad last updated on 25/Feb/18
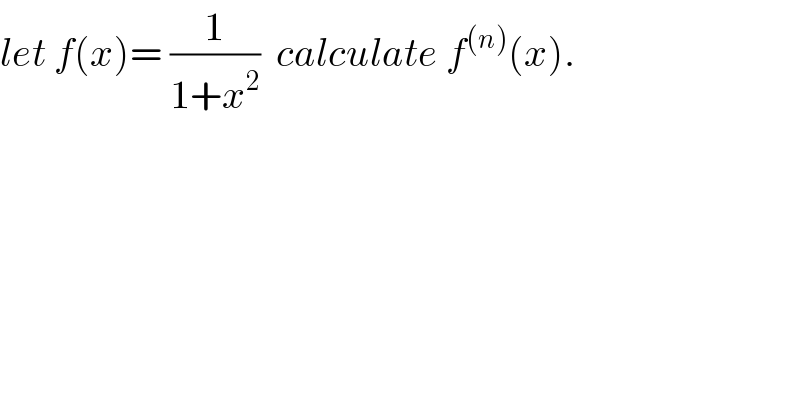
Commented by abdo imad last updated on 28/Feb/18
![we have f(x)= (1/((x+i)(x−i)))=(1/(2i))( (1/(x−i)) −(1/(x+i))) ⇒ f^((n)) (x)= (1/(2i))( ((1/(x−i)))^((n)) −((1/(x+i)))^((n)) ) =(1/(2i))( (((−1)^n n!)/((x−i)^(n+1) )) −(((−1)^n n!)/((x+i)^(n+1) ))) =((n!(−1)^n )/(2i))( (((x+i)^(n+1) −(x−i)^(n+1) )/((1+x^2 )^(n+1) ))) but (x+i)^(n+1) −(x−i)^(n+1) = Σ_(k=0) ^(n+1) C_(n+1) ^k i^k x^(n+1−k) −Σ_(k=0) ^(n+1) (−i)^k x^(n+1−k) =Σ_(k=0) ^(n+1) C_(n+1) ^k ( i^k −(−i)^k )x^(n+1−k) =Σ_(p=0) ^([(n/2)]) C_(n+1) ^(2p+1) (2i) x^(n+1−2p−1) ⇒ f^((n)) (x)=n! (−1)^n ((Σ_(p=0) ^([(n/2)]) C_(n+1) ^(2p+1) x^(n−2p) )/((1+x^2 )^(n+1) )) . also wecan give f^((n)) at form of arctan....](Q30908.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 30752 by abdo imad last updated on 25/Feb/18 | ||
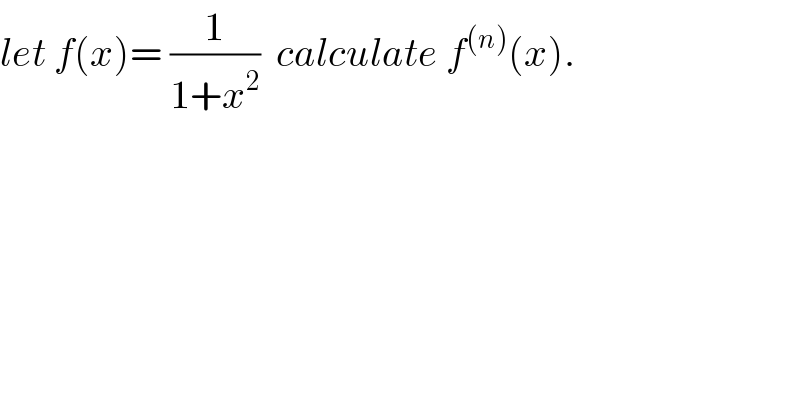 | ||
Commented by abdo imad last updated on 28/Feb/18 | ||
![we have f(x)= (1/((x+i)(x−i)))=(1/(2i))( (1/(x−i)) −(1/(x+i))) ⇒ f^((n)) (x)= (1/(2i))( ((1/(x−i)))^((n)) −((1/(x+i)))^((n)) ) =(1/(2i))( (((−1)^n n!)/((x−i)^(n+1) )) −(((−1)^n n!)/((x+i)^(n+1) ))) =((n!(−1)^n )/(2i))( (((x+i)^(n+1) −(x−i)^(n+1) )/((1+x^2 )^(n+1) ))) but (x+i)^(n+1) −(x−i)^(n+1) = Σ_(k=0) ^(n+1) C_(n+1) ^k i^k x^(n+1−k) −Σ_(k=0) ^(n+1) (−i)^k x^(n+1−k) =Σ_(k=0) ^(n+1) C_(n+1) ^k ( i^k −(−i)^k )x^(n+1−k) =Σ_(p=0) ^([(n/2)]) C_(n+1) ^(2p+1) (2i) x^(n+1−2p−1) ⇒ f^((n)) (x)=n! (−1)^n ((Σ_(p=0) ^([(n/2)]) C_(n+1) ^(2p+1) x^(n−2p) )/((1+x^2 )^(n+1) )) . also wecan give f^((n)) at form of arctan....](Q30908.png) | ||