
Question and Answers Forum
Question Number 30757 by abdo imad last updated on 25/Feb/18
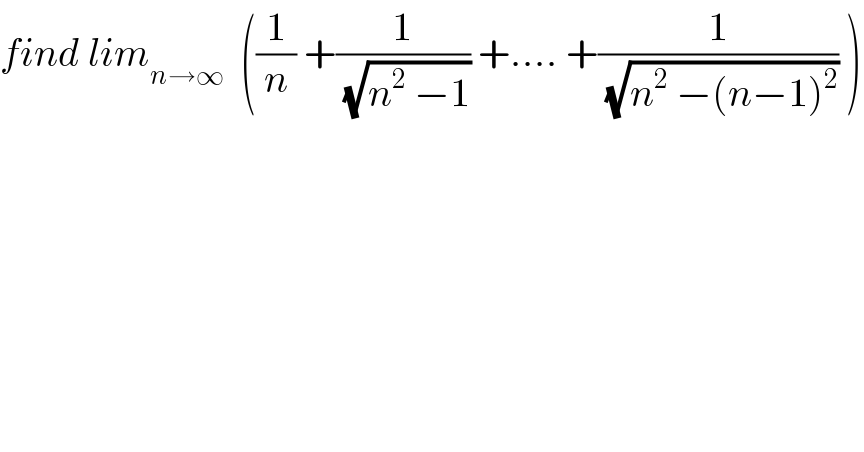
Commented by abdo imad last updated on 28/Feb/18
![let put w_n = (1/n) +(1/(√(n^2 −1))) +...+(1/(√(n^2 −(n−1)^2 ))) w_n =(1/n)( 1+(1/(√(1−(1^2 /n^2 )))) +(1/(√(1−(2^2 /n^2 )))) +..... + (1/(√(1−(((n−1)^2 )/n^2 ))))) = (1/n)Σ_(k=0) ^(n−1) (1/(√(1 −((k/n))^2 ))) so w_n is a Rieman sum and lim_(n→∞) w_n = ∫_0 ^1 (dx/(√(1−x^2 ))) =[arcsinx]_0 ^1 =(π/2) .](Q30906.png)
| ||
Question and Answers Forum | ||
Question Number 30757 by abdo imad last updated on 25/Feb/18 | ||
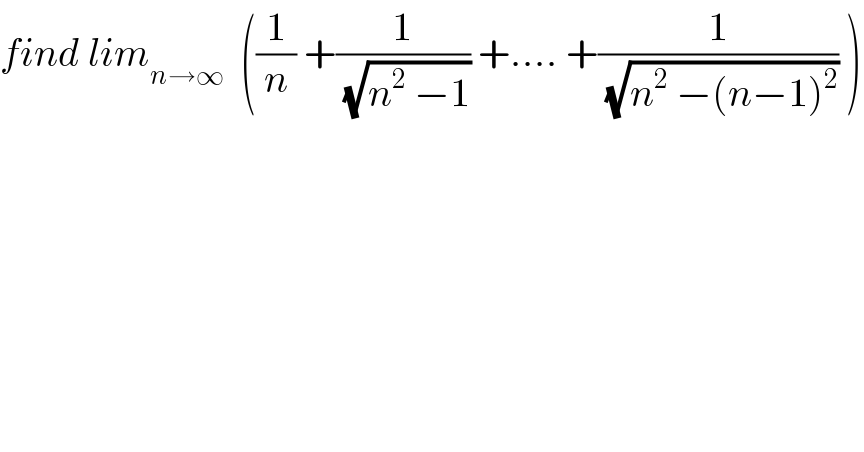 | ||
Commented by abdo imad last updated on 28/Feb/18 | ||
![let put w_n = (1/n) +(1/(√(n^2 −1))) +...+(1/(√(n^2 −(n−1)^2 ))) w_n =(1/n)( 1+(1/(√(1−(1^2 /n^2 )))) +(1/(√(1−(2^2 /n^2 )))) +..... + (1/(√(1−(((n−1)^2 )/n^2 ))))) = (1/n)Σ_(k=0) ^(n−1) (1/(√(1 −((k/n))^2 ))) so w_n is a Rieman sum and lim_(n→∞) w_n = ∫_0 ^1 (dx/(√(1−x^2 ))) =[arcsinx]_0 ^1 =(π/2) .](Q30906.png) | ||