
Question and Answers Forum
Question Number 30769 by abdo imad last updated on 25/Feb/18
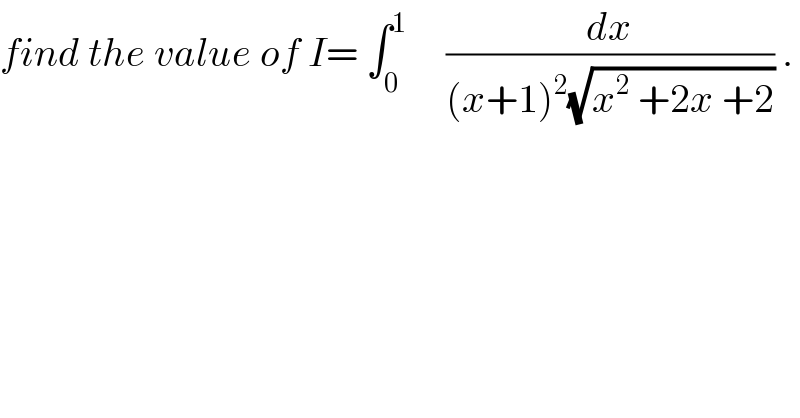
Commented by abdo imad last updated on 27/Feb/18
![we have x^2 +2x+2=(x+1)^2 +1 the ch=x+1=t give I= ∫_1 ^2 (dt/(t^2 (√(1+t^2 )))) the we can use the ch.t=tanθ ⇒ I= ∫_(π/4) ^(artan2) ((1+tan^2 θ)/(tan^2 θ(√(1+tan^2 θ))))dθ = ∫_(π/4) ^(arctan2) ((cos^2 θ)/(sin^2 θ)) (1/(cosθ))dθ = ∫_(π/4) ^(arctan2) ((cosθ)/(sin^2 θ)) dθ =[−(1/(sinθ))]_(π/4) ^(arctan2) =(√2) − (1/(sin(arctan2))) but we have the formula sin(arctanx)= (x/(√(1+x^2 )))( for proof put x=tanθ)⇒ sin(arctan2)= (2/(√5)) ⇒ I=(√2) −(2/(√5)) .](Q30884.png)
| ||
Question and Answers Forum | ||
Question Number 30769 by abdo imad last updated on 25/Feb/18 | ||
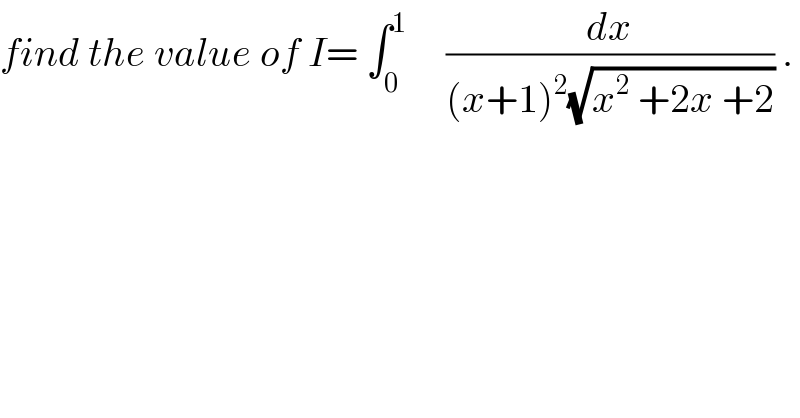 | ||
Commented by abdo imad last updated on 27/Feb/18 | ||
![we have x^2 +2x+2=(x+1)^2 +1 the ch=x+1=t give I= ∫_1 ^2 (dt/(t^2 (√(1+t^2 )))) the we can use the ch.t=tanθ ⇒ I= ∫_(π/4) ^(artan2) ((1+tan^2 θ)/(tan^2 θ(√(1+tan^2 θ))))dθ = ∫_(π/4) ^(arctan2) ((cos^2 θ)/(sin^2 θ)) (1/(cosθ))dθ = ∫_(π/4) ^(arctan2) ((cosθ)/(sin^2 θ)) dθ =[−(1/(sinθ))]_(π/4) ^(arctan2) =(√2) − (1/(sin(arctan2))) but we have the formula sin(arctanx)= (x/(√(1+x^2 )))( for proof put x=tanθ)⇒ sin(arctan2)= (2/(√5)) ⇒ I=(√2) −(2/(√5)) .](Q30884.png) | ||