
Question and Answers Forum
Question Number 30773 by abdo imad last updated on 25/Feb/18
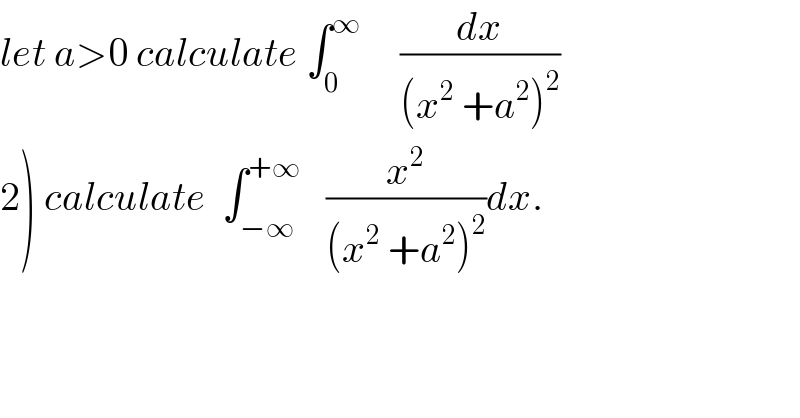
Commented byabdo imad last updated on 26/Feb/18
![1)the ch. x=a tant give I=∫_0 ^∞ (dx/((x^2 +a^2 )^2 )) = ∫_0 ^(π/2) (1/(a^4 (1+tan^2 t)^2 )) a(1+tan^2 t)dt =(1/a^3 ) ∫_0 ^(π/2) (dt/(1+tan^2 t))⇒a^3 I= ∫_0 ^(π/2) cos^2 tdt = ∫_0 ^(π/2) ((1+cos(2t))/2)dt=(π/4) +[(1/4) sin(2t)]_0 ^(π/2) =(π/4) ⇒ I=(π/(4 a^3 )) 2) let put J= ∫_(−∞) ^(+∞) (x^2 /((x^2 +a^2 )^2 ))dx J= 2∫_0 ^∞ ((x^2 +a^(2 ) −a^2 )/((x^2 +a^2 )^2 ))dx =2∫_0 ^∞ (dx/((x^2 +a^2 )))dx −2a^2 ∫_0 ^∞ (dx/((x^2 +a^2 )^2 ))dx ch x=at ⇒ ∫_0 ^∞ (dx/((x^2 +a^2 )))= ∫_0 ^∞ ((adt)/(a^2 (1+t^2 )))=(1/a)(π/2)= (π/(2a)) J=(π/a) −2a^2 I = (π/a) −2a^2 (π/(4a^3 ))= (π/a) −(π/(2a))⇒ J=(π/(2a)) .](Q30847.png)
| ||
Question and Answers Forum | ||
Question Number 30773 by abdo imad last updated on 25/Feb/18 | ||
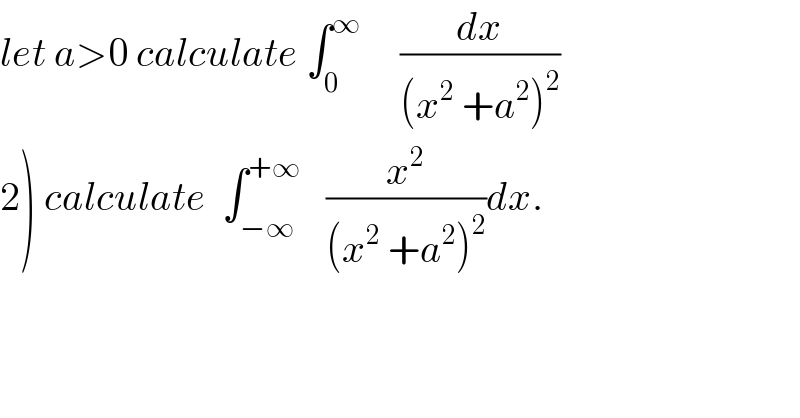 | ||
Commented byabdo imad last updated on 26/Feb/18 | ||
![1)the ch. x=a tant give I=∫_0 ^∞ (dx/((x^2 +a^2 )^2 )) = ∫_0 ^(π/2) (1/(a^4 (1+tan^2 t)^2 )) a(1+tan^2 t)dt =(1/a^3 ) ∫_0 ^(π/2) (dt/(1+tan^2 t))⇒a^3 I= ∫_0 ^(π/2) cos^2 tdt = ∫_0 ^(π/2) ((1+cos(2t))/2)dt=(π/4) +[(1/4) sin(2t)]_0 ^(π/2) =(π/4) ⇒ I=(π/(4 a^3 )) 2) let put J= ∫_(−∞) ^(+∞) (x^2 /((x^2 +a^2 )^2 ))dx J= 2∫_0 ^∞ ((x^2 +a^(2 ) −a^2 )/((x^2 +a^2 )^2 ))dx =2∫_0 ^∞ (dx/((x^2 +a^2 )))dx −2a^2 ∫_0 ^∞ (dx/((x^2 +a^2 )^2 ))dx ch x=at ⇒ ∫_0 ^∞ (dx/((x^2 +a^2 )))= ∫_0 ^∞ ((adt)/(a^2 (1+t^2 )))=(1/a)(π/2)= (π/(2a)) J=(π/a) −2a^2 I = (π/a) −2a^2 (π/(4a^3 ))= (π/a) −(π/(2a))⇒ J=(π/(2a)) .](Q30847.png) | ||