
Question and Answers Forum
Question Number 30774 by abdo imad last updated on 25/Feb/18

Commented byabdo imad last updated on 26/Feb/18
![let put (√t) x=u ⇒f(t)= ∫_0 ^(√t) ln(1+u^2 )(du/(√t)) =(1/(√t)) ∫_0 ^(√t) ln(1+u^2 )du but we have by parts ∫_0 ^(√t) ln(1+u^2 )du= [uln(1+u^2 )]_0 ^(√t) −∫_0 ^(√t) u((2u)/(1+u^2 ))du =(√t) ln(1+t) −2∫_0 ^(√t) ((1+u^2 −1)/(1+u^2 ))du =(√t) ln(1+t) −2(√t) +2 ∫_0 ^(√t) (du/(1+u^2 )) =(√t) ln(1+t)−2(√t) +2 arctan((√t))⇒ f(t)= ln(1+t) +((2 arctan((√t)))/(√t)) −2 .](Q30846.png)
Answered by sma3l2996 last updated on 25/Feb/18
![let u=tx f(t)=∫_0 ^t ln(1+u^2 )du =[uln(1+u^2 )]_0 ^t −2∫_0 ^t (u^2 /(1+u^2 ))du =tln(1+t^2 )−2∫_0 ^t (1−(1/(1+u^2 )))du =tln(1+t^2 )−2[u−tan^(−1) (u)]_0 ^t f(t)=tln(1+t^2 )−2t+2tan^(−1) (t)](Q30788.png)
Commented byabdo imad last updated on 26/Feb/18
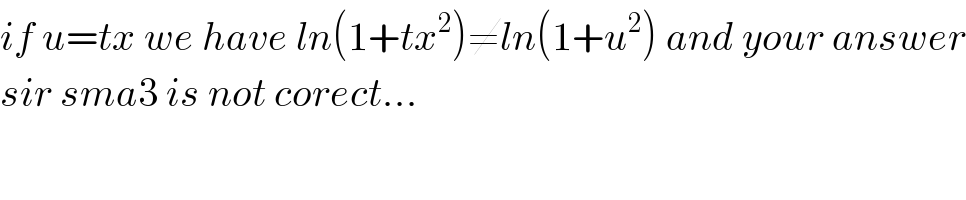
| ||
Question and Answers Forum | ||
Question Number 30774 by abdo imad last updated on 25/Feb/18 | ||
 | ||
Commented byabdo imad last updated on 26/Feb/18 | ||
![let put (√t) x=u ⇒f(t)= ∫_0 ^(√t) ln(1+u^2 )(du/(√t)) =(1/(√t)) ∫_0 ^(√t) ln(1+u^2 )du but we have by parts ∫_0 ^(√t) ln(1+u^2 )du= [uln(1+u^2 )]_0 ^(√t) −∫_0 ^(√t) u((2u)/(1+u^2 ))du =(√t) ln(1+t) −2∫_0 ^(√t) ((1+u^2 −1)/(1+u^2 ))du =(√t) ln(1+t) −2(√t) +2 ∫_0 ^(√t) (du/(1+u^2 )) =(√t) ln(1+t)−2(√t) +2 arctan((√t))⇒ f(t)= ln(1+t) +((2 arctan((√t)))/(√t)) −2 .](Q30846.png) | ||
Answered by sma3l2996 last updated on 25/Feb/18 | ||
![let u=tx f(t)=∫_0 ^t ln(1+u^2 )du =[uln(1+u^2 )]_0 ^t −2∫_0 ^t (u^2 /(1+u^2 ))du =tln(1+t^2 )−2∫_0 ^t (1−(1/(1+u^2 )))du =tln(1+t^2 )−2[u−tan^(−1) (u)]_0 ^t f(t)=tln(1+t^2 )−2t+2tan^(−1) (t)](Q30788.png) | ||
| ||
Commented byabdo imad last updated on 26/Feb/18 | ||
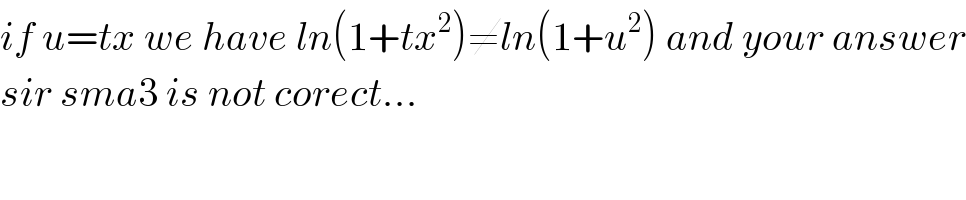 | ||