Math Question and Answers


Question and Answers Forum

All Questions Topic List
Coordinate Geometry Questions
Previous in All Question Next in All Question
Previous in Coordinate Geometry Next in Coordinate Geometry
Question Number 30820 by ajfour last updated on 26/Feb/18

	Answered by mrW2 last updated on 26/Feb/18
	$Eqn. of ellipse 1 (original one): (x^2 /a^2 )+(y^2 /b^2 )=1 ((r^2 cos^2 ϕ)/a^2 )+((r^2 sin^2 ϕ)/b^2 )=1 ⇒r^2 [((cos^2 ϕ)/a^2 )+((sin^2 ϕ)/b^2 )]=1 ⇒r^2 =((a^2 b^2 )/(a^2 sin^2 ϕ+b^2 cos^2 ϕ)) Eqn. of ellipse 2 (rotated one): ⇒r^2 [((cos^2 (ϕ−θ))/a^2 )+((sin^2 (ϕ−θ))/b^2 )]=1 ⇒r^2 =((a^2 b^2 )/(a^2 sin^2 (ϕ−θ)+b^2 cos^2 (ϕ−θ))) Intersection of both ellipses: ((cos^2 ϕ)/a^2 )+((sin^2 ϕ)/b^2 )=((cos^2 (ϕ−θ))/a^2 )+((sin^2 (ϕ−θ))/b^2 ) b^2 cos^2 ϕ+a^2 sin^2 ϕ=b^2 cos^2 (ϕ−θ)+a^2 sin^2 (ϕ−θ) b^2 cos^2 ϕ+a^2 sin^2 ϕ=b^2 (cos ϕ cos θ+sin ϕ sin θ)^2 +a^2 (sin ϕ cos θ−cos ϕ sin θ)^2 b^2 cos^2 ϕ+a^2 sin^2 ϕ=b^2 cos^2 ϕ cos^2 θ+b^2 sin^2 ϕ sin^2 θ+2b^2 sin ϕ cos ϕ sin θ cos θ+a^2 sin^2 ϕ cos^2 θ+a^2 cos^2 ϕ sin^2 θ−2a^2 sin ϕ cos ϕ sin θ cos θ b^2 (cos^2 ϕ−sin^2 ϕ) sin^2 θ−a^2 (cos^2 ϕ−sin^2 ϕ) sin^2 θ=2(b^2 −a^2 ) sin ϕ cos ϕ sin θ cos θ (b^2 −a^2 )cos 2ϕ sin^2 θ=(b^2 −a^2 ) sin 2ϕ sin θ cos θ cos 2ϕ sin θ= sin 2ϕ cos θ ⇒tan 2ϕ=tan θ ⇒2ϕ=θ or θ+π ⇒ϕ_1 =(θ/2) ⇒ϕ_2 =(θ/2)+(π/2) A=∫_ϕ_1 ^( ϕ_2 ) ∫_r_1 ^r_2 rdrdϕ =(1/2)∫_ϕ_1 ^( ϕ_2 ) [r_2 ^2 −r_1 ^2 ]dϕ =((a^2 b^2 )/2)∫_ϕ_1 ^( ϕ_2 ) [(1/(a^2 sin^2 (ϕ−θ)+b^2 cos^2 (ϕ−θ)))−(1/(a^2 sin^2 ϕ+b^2 cos^2 ϕ))]dϕ =((a^2 b^2 )/2)[(1/(ab))tan^(−1) {(a/b) tan (ϕ−θ)}−(1/(ab))tan^(−1) {(a/b) tan ϕ}]_ϕ_1 ^ϕ_2 =((ab)/2)[tan^(−1) {(a/b) tan (ϕ−θ)}−tan^(−1) {(a/b) tan ϕ}]_ϕ_1 ^ϕ_2 =((ab)/2)[tan^(−1) {(a/b) tan ((π/2)−(θ/2))}−tan^(−1) {(a/b) tan ((π/2)+(θ/2))}−tan^(−1) {(a/b) tan ((θ/2)−θ)}+tan^(−1) {(a/b) tan (θ/2)}] =((ab)/2)[2 tan^(−1) {(a/b) tan ((π/2)−(θ/2))}−π+2 tan^(−1) {(a/b) tan (θ/2)}] =ab[tan^(−1) {(a/b) tan ((π/2)−(θ/2))}+tan^(−1) {(a/b) tan (θ/2)}−(π/2)] =ab{(π/2)− tan^(−1) [((2ab)/((a^2 −b^2 )sin θ))]} ⇒A=ab tan^(−1) ∣(((a^2 −b^2 )sin θ)/(2ab))∣ An other way: A=(1/2)(πab−4∫_ϕ_1 ^( ϕ_2 ) (r_1 ^2 /2)dϕ) =ab(π/2)−∫_ϕ_1 ^( ϕ_2 ) ((a^2 b^2 )/(a^2 sin^2 ϕ+b^2 cos^2 ϕ))dϕ =ab(π/2)−a^2 b^2 [(1/(ab)) tan^(−1) {(a/b)tan ϕ}]_ϕ_1 ^ϕ_2 =ab(π/2)−ab[tan^(−1) {(a/b)tan ((π/2)+(θ/2))}−tan^(−1) {(a/b)tan ((θ/2))}] =ab(π/2)−ab[π−tan^(−1) {(a/b)tan ((π/2)−(θ/2))}−tan^(−1) {(a/b)tan ((θ/2))}] =ab[tan^(−1) {(a/b)tan ((π/2)−(θ/2))}+tan^(−1) {(a/b)tan ((θ/2))}−(π/2)] ..... as above$
	$E q n . o f e l l i p s e 1 (o r i g i n a l o n e) :$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $\frac{r^{2} \cos^{2} φ}{a^{2}} + \frac{r^{2} \sin^{2} φ}{b^{2}} = 1$ $\Rightarrow r^{2} [\frac{\cos^{2} φ}{a^{2}} + \frac{\sin^{2} φ}{b^{2}}] = 1$ $\Rightarrow r^{2} = \frac{a^{2} b^{2}}{a^{2} \sin^{2} φ + b^{2} \cos^{2} φ}$ $E q n . o f e l l i p s e 2 (r o t a t e d o n e) :$ $\Rightarrow r^{2} [\frac{\cos^{2} (φ - θ)}{a^{2}} + \frac{\sin^{2} (φ - θ)}{b^{2}}] = 1$ $\Rightarrow r^{2} = \frac{a^{2} b^{2}}{a^{2} \sin^{2} (φ - θ) + b^{2} \cos^{2} (φ - θ)}$ $I n t e r s e c t i o n o f b o t h e l l i p s e s :$ $\frac{\cos^{2} φ}{a^{2}} + \frac{\sin^{2} φ}{b^{2}} = \frac{\cos^{2} (φ - θ)}{a^{2}} + \frac{\sin^{2} (φ - θ)}{b^{2}}$ $b^{2} \cos^{2} φ + a^{2} \sin^{2} φ = b^{2} \cos^{2} (φ - θ) + a^{2} \sin^{2} (φ - θ)$ $b^{2} \cos^{2} φ + a^{2} \sin^{2} φ = b^{2} {(\cos φ \cos θ + \sin φ \sin θ)}^{2} + a^{2} {(\sin φ \cos θ - \cos φ \sin θ)}^{2}$ $b^{2} \cos^{2} φ + a^{2} \sin^{2} φ = b^{2} \cos^{2} φ \cos^{2} θ + b^{2} \sin^{2} φ \sin^{2} θ + 2 b^{2} \sin φ \cos φ \sin θ \cos θ + a^{2} \sin^{2} φ \cos^{2} θ + a^{2} \cos^{2} φ \sin^{2} θ - 2 a^{2} \sin φ \cos φ \sin θ \cos θ$ $b^{2} (\cos^{2} φ - \sin^{2} φ) \sin^{2} θ - a^{2} (\cos^{2} φ - \sin^{2} φ) \sin^{2} θ = 2 (b^{2} - a^{2}) \sin φ \cos φ \sin θ \cos θ$ $(b^{2} - a^{2}) \cos 2 φ \sin^{2} θ = (b^{2} - a^{2}) \sin 2 φ \sin θ \cos θ$ $\cos 2 φ \sin θ = \sin 2 φ \cos θ$ $\Rightarrow \tan 2 φ = \tan θ$ $\Rightarrow 2 φ = θ o r θ + π$ $\Rightarrow φ_{1} = \frac{θ}{2}$ $\Rightarrow φ_{2} = \frac{θ}{2} + \frac{π}{2}$ $A = \int_{φ_{1}}^{φ_{2}} \int_{r_{1}}^{r_{2}} r d r d φ$ $= \frac{1}{2} \int_{φ_{1}}^{φ_{2}} [r_{2}^{2} - r_{1}^{2}] d φ$ $= \frac{a^{2} b^{2}}{2} \int_{φ_{1}}^{φ_{2}} [\frac{1}{a^{2} \sin^{2} (φ - θ) + b^{2} \cos^{2} (φ - θ)} - \frac{1}{a^{2} \sin^{2} φ + b^{2} \cos^{2} φ}] d φ$ $= \frac{a^{2} b^{2}}{2} {[\frac{1}{a b} \tan^{- 1} {\frac{a}{b} \tan (φ - θ)} - \frac{1}{a b} \tan^{- 1} {\frac{a}{b} \tan φ}]}_{φ_{1}}^{φ_{2}}$ $= \frac{a b}{2} {[\tan^{- 1} {\frac{a}{b} \tan (φ - θ)} - \tan^{- 1} {\frac{a}{b} \tan φ}]}_{φ_{1}}^{φ_{2}}$ $= \frac{a b}{2} [\tan^{- 1} {\frac{a}{b} \tan (\frac{π}{2} - \frac{θ}{2})} - \tan^{- 1} {\frac{a}{b} \tan (\frac{π}{2} + \frac{θ}{2})} - \tan^{- 1} {\frac{a}{b} \tan (\frac{θ}{2} - θ)} + \tan^{- 1} {\frac{a}{b} \tan \frac{θ}{2}}]$ $= \frac{a b}{2} [2 \tan^{- 1} {\frac{a}{b} \tan (\frac{π}{2} - \frac{θ}{2})} - π + 2 \tan^{- 1} {\frac{a}{b} \tan \frac{θ}{2}}]$ $= a b [\tan^{- 1} {\frac{a}{b} \tan (\frac{π}{2} - \frac{θ}{2})} + \tan^{- 1} {\frac{a}{b} \tan \frac{θ}{2}} - \frac{π}{2}]$ $= a b {\frac{π}{2} - \tan^{- 1} [\frac{2 a b}{(a^{2} - b^{2}) \sin θ}]}$ $\Rightarrow A = a b \tan^{- 1} ∣ \frac{(a^{2} - b^{2}) \sin θ}{2 a b} ∣$ $A n o t h e r w a y :$ $A = \frac{1}{2} (π a b - 4 \int_{φ_{1}}^{φ_{2}} \frac{r_{1}^{2}}{2} d φ)$ $= a b \frac{π}{2} - \int_{φ_{1}}^{φ_{2}} \frac{a^{2} b^{2}}{a^{2} \sin^{2} φ + b^{2} \cos^{2} φ} d φ$ $= a b \frac{π}{2} - a^{2} b^{2} {[\frac{1}{a b} \tan^{- 1} {\frac{a}{b} \tan φ}]}_{φ_{1}}^{φ_{2}}$ $= a b \frac{π}{2} - a b [\tan^{- 1} {\frac{a}{b} \tan (\frac{π}{2} + \frac{θ}{2})} - \tan^{- 1} {\frac{a}{b} \tan (\frac{θ}{2})}]$ $= a b \frac{π}{2} - a b [π - \tan^{- 1} {\frac{a}{b} \tan (\frac{π}{2} - \frac{θ}{2})} - \tan^{- 1} {\frac{a}{b} \tan (\frac{θ}{2})}]$ $= a b [\tan^{- 1} {\frac{a}{b} \tan (\frac{π}{2} - \frac{θ}{2})} + \tan^{- 1} {\frac{a}{b} \tan (\frac{θ}{2})} - \frac{π}{2}]$ $. . . . . a s a b o v e$
	Commented by ajfour last updated on 26/Feb/18

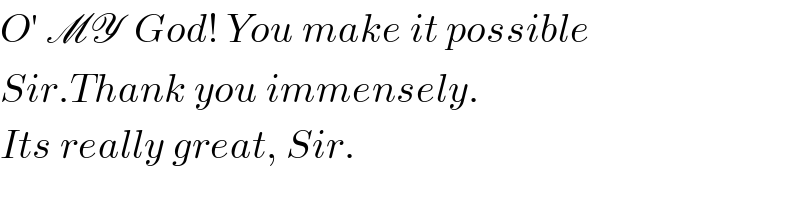
	$O^{'} MY G o d! Y o u m a k e i t p o s s i b l e$ $S i r . T h a n k y o u i m m e n s e l y .$ $I t s r e a l l y g r e a t, S i r .$
	Commented by ajfour last updated on 26/Feb/18

	$Y e s S i r, t h a n k y o u a g a i n .$
	Commented by mrW2 last updated on 26/Feb/18

	$T h a n k s f o r c h e c k i n g!$ $I c h e c k e d a g a i n . T h e f i n a l f o r m u l a i s$ $A = a b \tan^{- 1} ∣ \frac{(a^{2} - b^{2}) \sin θ}{2 a b} ∣$ ${I t}^{'} s m o r e s i m p l e t h a n I^{'} v e e x p e c t e d .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum