Question Number 30849 by Penguin last updated on 27/Feb/18
![x^7 +x^6 +x^5 +x^4 +x^3 +x^2 +x+1=0 Σ_(k=1) ^7 [ℜ(x_k )]^2 = ? x_k = k^( th) root of the equation ℜ(x_k ) = real part of the root](Q30849.png)
$${x}^{\mathrm{7}} +{x}^{\mathrm{6}} +{x}^{\mathrm{5}} +{x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0} \\ $$$$\: \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{7}} {\sum}}\left[\Re\left({x}_{{k}} \right)\right]^{\mathrm{2}} \:=\:? \\ $$$${x}_{{k}} \:=\:{k}^{\:\mathrm{th}} \:\mathrm{root}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\Re\left({x}_{{k}} \right)\:=\:\mathrm{real}\:\mathrm{part}\:\mathrm{of}\:\mathrm{the}\:\mathrm{root} \\ $$
Commented by prof Abdo imad last updated on 27/Feb/18
![z root for this equation ⇔ z^8 =1 and z≠o the roots of this equation are z_k =e^(i((kπ)/4)) and k∈[[1,7]] ⇒ Re(z_k ) = cos(((kπ)/4))⇒ (Re(z_k ))^2 =cos^2 (((kπ)/4)) and Σ_(k=1) ^7 (Re(z_k ))^2 = Σ_(k=1) ^7 ((1+cos(((kπ)/2)))/2) =(7/2) +(1/2) Σ_(k=1) ^(7 ) cos(((kπ)/2)) but Σ_(k=1) ^7 cos(((kπ)/2))=Σ_(k=0) ^7 cos(((kπ)/2)) −1 =Re( Σ_(k=0) ^7 e^(i((kπ)/2)) )−1 Re( ((1−(e^(i(π/2)) )^8 )/(1−e^(i(π/2)) )))−1=0−1=−1⇒ Σ_(k=1) ^7 (Re(z_k ))^2 =(7/2) −(1/2) =3.](Q30850.png)
$${z}\:{root}\:{for}\:{this}\:{equation}\:\Leftrightarrow\:{z}^{\mathrm{8}} =\mathrm{1}\:{and}\:{z}\neq{o}\: \\ $$$${the}\:{roots}\:{of}\:{this}\:{equation}\:{are}\:{z}_{{k}} \:={e}^{{i}\frac{{k}\pi}{\mathrm{4}}} \:\:{and} \\ $$$${k}\in\left[\left[\mathrm{1},\mathrm{7}\right]\right]\:\Rightarrow\:{Re}\left({z}_{{k}} \right)\:=\:{cos}\left(\frac{{k}\pi}{\mathrm{4}}\right)\Rightarrow \\ $$$$\left({Re}\left({z}_{{k}} \right)\right)^{\mathrm{2}} ={cos}^{\mathrm{2}} \left(\frac{{k}\pi}{\mathrm{4}}\right)\:{and} \\ $$$$\sum_{{k}=\mathrm{1}} ^{\mathrm{7}} \:\left({Re}\left({z}_{{k}} \right)\right)^{\mathrm{2}} =\:\sum_{{k}=\mathrm{1}} ^{\mathrm{7}} \frac{\mathrm{1}+{cos}\left(\frac{{k}\pi}{\mathrm{2}}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{7}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{k}=\mathrm{1}} ^{\mathrm{7}\:} \:{cos}\left(\frac{{k}\pi}{\mathrm{2}}\right)\:{but} \\ $$$$\sum_{{k}=\mathrm{1}} ^{\mathrm{7}} \:{cos}\left(\frac{{k}\pi}{\mathrm{2}}\right)=\sum_{{k}=\mathrm{0}} ^{\mathrm{7}} \:{cos}\left(\frac{{k}\pi}{\mathrm{2}}\right)\:−\mathrm{1} \\ $$$$={Re}\left(\:\sum_{{k}=\mathrm{0}} ^{\mathrm{7}} \:{e}^{{i}\frac{{k}\pi}{\mathrm{2}}} \right)−\mathrm{1} \\ $$$${Re}\left(\:\frac{\mathrm{1}−\left({e}^{{i}\frac{\pi}{\mathrm{2}}} \right)^{\mathrm{8}} }{\mathrm{1}−{e}^{{i}\frac{\pi}{\mathrm{2}}} }\right)−\mathrm{1}=\mathrm{0}−\mathrm{1}=−\mathrm{1}\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{\mathrm{7}} \left({Re}\left({z}_{{k}} \right)\right)^{\mathrm{2}} =\frac{\mathrm{7}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:=\mathrm{3}. \\ $$$$ \\ $$
Commented by Penguin last updated on 27/Feb/18
$$\sum_{{k}=\mathrm{1}} ^{\mathrm{7}} \:\left({Re}\left({z}_{{k}} \right)\right)^{\mathrm{2}} =\:\sum_{{k}=\mathrm{1}} ^{\mathrm{7}} \frac{\mathrm{1}+{cos}\left(\frac{{k}\pi}{\mathrm{2}}\right)}{\mathrm{2}} \\ $$$$\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{get}\:\mathrm{this}\:\mathrm{result}? \\ $$
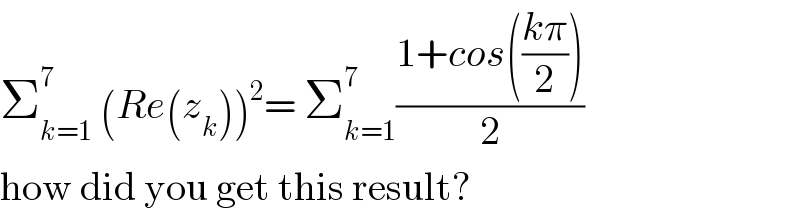
Commented by MJS last updated on 27/Feb/18
![I tried to solve it, must admit that this might not always be possible (but I always love to try...) x_1 =−1 x_2 =−i x_3 =i x_4 =−((√2)/2)−((√2)/2)i x_5 =−((√2)/2)+((√2)/2)i x_6 =((√2)/2)−((√2)/2)i x_7 =((√2)/2)+((√2)/2)i Σ_(k=1) ^7 [ℜ(x_k )]^2 = 3](Q30874.png)
$$\mathrm{I}\:\mathrm{tried}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{it},\:\mathrm{must}\:\mathrm{admit}\:\mathrm{that} \\ $$$$\mathrm{this}\:\mathrm{might}\:\mathrm{not}\:\mathrm{always}\:\mathrm{be}\:\mathrm{possible} \\ $$$$\left(\mathrm{but}\:\mathrm{I}\:\mathrm{always}\:\mathrm{love}\:\mathrm{to}\:\mathrm{try}...\right) \\ $$$${x}_{\mathrm{1}} =−\mathrm{1} \\ $$$${x}_{\mathrm{2}} =−\mathrm{i} \\ $$$${x}_{\mathrm{3}} =\mathrm{i} \\ $$$${x}_{\mathrm{4}} =−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{i} \\ $$$${x}_{\mathrm{5}} =−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{i} \\ $$$${x}_{\mathrm{6}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{i} \\ $$$${x}_{\mathrm{7}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{i} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{7}} {\sum}}\left[\Re\left({x}_{{k}} \right)\right]^{\mathrm{2}} \:=\:\mathrm{3} \\ $$
Commented by rahul 19 last updated on 27/Feb/18
$${yahh},\:{short}\:{methods}! \\ $$
Commented by abdo imad last updated on 28/Feb/18
$${look}\:{my}\:{proof}\:{i}\:{have}\:{used}\:{the}\:{formula}\:{cos}^{\mathrm{2}} \alpha=\frac{\mathrm{1}+{cos}\left(\mathrm{2}\alpha\right)}{\mathrm{2}}\:. \\ $$