Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 31074 by abdo imad last updated on 02/Mar/18

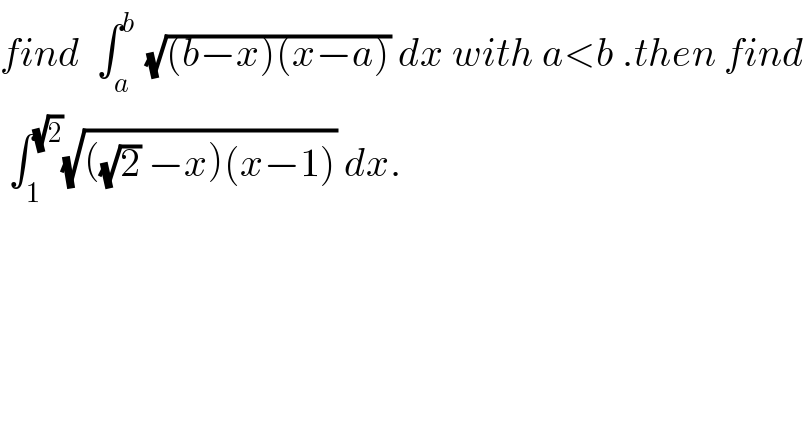
find ∫_a ^b (√((b−x)(x−a))) dx with a<b .then find ∫_1 ^(√2) (√(((√2) −x)(x−1))) dx.

$${find}\:\:\int_{{a}} ^{{b}} \:\sqrt{\left({b}−{x}\right)\left({x}−{a}\right)}\:{dx}\:{with}\:{a}<{b}\:.{then}\:{find}\: \\ $$ $$\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \sqrt{\left(\sqrt{\mathrm{2}}\:−{x}\right)\left({x}−\mathrm{1}\right)}\:{dx}. \\ $$

Commented byabdo imad last updated on 09/Mar/18

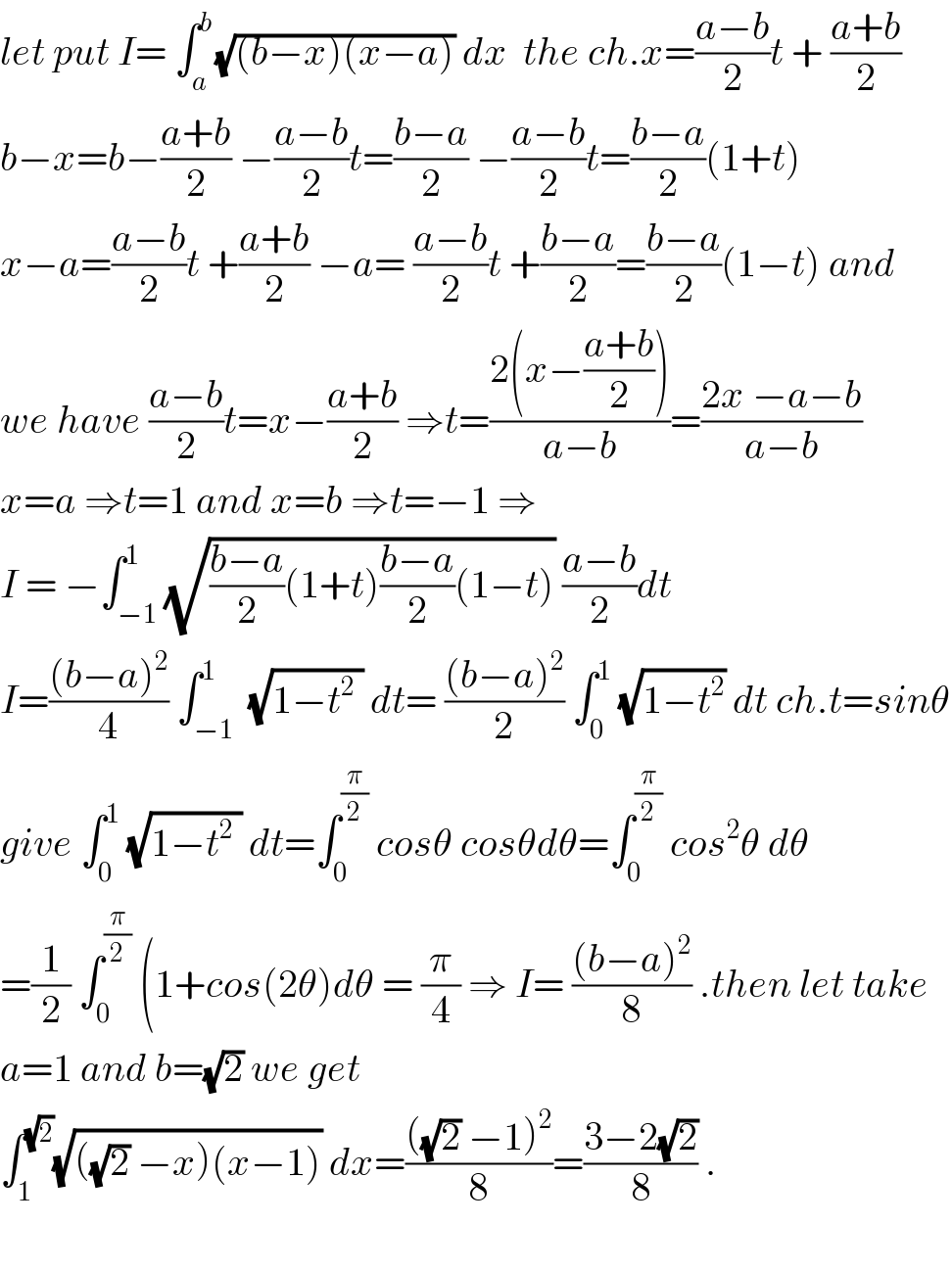
let put I= ∫_a ^b (√((b−x)(x−a))) dx the ch.x=((a−b)/2)t + ((a+b)/2) b−x=b−((a+b)/2) −((a−b)/2)t=((b−a)/2) −((a−b)/2)t=((b−a)/2)(1+t) x−a=((a−b)/2)t +((a+b)/2) −a= ((a−b)/2)t +((b−a)/2)=((b−a)/2)(1−t) and we have ((a−b)/2)t=x−((a+b)/2) ⇒t=((2(x−((a+b)/2)))/(a−b))=((2x −a−b)/(a−b)) x=a ⇒t=1 and x=b ⇒t=−1 ⇒ I = −∫_(−1) ^(1 ) (√(((b−a)/2)(1+t)((b−a)/2)(1−t))) ((a−b)/2)dt I=(((b−a)^2 )/4) ∫_(−1) ^1 (√(1−t^2 )) dt= (((b−a)^2 )/2) ∫_0 ^1 (√(1−t^2 )) dt ch.t=sinθ give ∫_0 ^1 (√(1−t^2 )) dt=∫_0 ^(π/2) cosθ cosθdθ=∫_0 ^(π/2) cos^2 θ dθ =(1/2) ∫_0 ^(π/2) (1+cos(2θ)dθ = (π/4) ⇒ I= (((b−a)^2 )/8) .then let take a=1 and b=(√2) we get ∫_1 ^(√2) (√(((√2) −x)(x−1))) dx=((((√2) −1)^2 )/8)=((3−2(√2))/8) .

$${let}\:{put}\:{I}=\:\int_{{a}} ^{{b}} \sqrt{\left({b}−{x}\right)\left({x}−{a}\right)}\:{dx}\:\:{the}\:{ch}.{x}=\frac{{a}−{b}}{\mathrm{2}}{t}\:+\:\frac{{a}+{b}}{\mathrm{2}} \\ $$ $${b}−{x}={b}−\frac{{a}+{b}}{\mathrm{2}}\:−\frac{{a}−{b}}{\mathrm{2}}{t}=\frac{{b}−{a}}{\mathrm{2}}\:−\frac{{a}−{b}}{\mathrm{2}}{t}=\frac{{b}−{a}}{\mathrm{2}}\left(\mathrm{1}+{t}\right) \\ $$ $${x}−{a}=\frac{{a}−{b}}{\mathrm{2}}{t}\:+\frac{{a}+{b}}{\mathrm{2}}\:−{a}=\:\frac{{a}−{b}}{\mathrm{2}}{t}\:+\frac{{b}−{a}}{\mathrm{2}}=\frac{{b}−{a}}{\mathrm{2}}\left(\mathrm{1}−{t}\right)\:{and} \\ $$ $${we}\:{have}\:\frac{{a}−{b}}{\mathrm{2}}{t}={x}−\frac{{a}+{b}}{\mathrm{2}}\:\Rightarrow{t}=\frac{\mathrm{2}\left({x}−\frac{{a}+{b}}{\mathrm{2}}\right)}{{a}−{b}}=\frac{\mathrm{2}{x}\:−{a}−{b}}{{a}−{b}} \\ $$ $${x}={a}\:\Rightarrow{t}=\mathrm{1}\:{and}\:{x}={b}\:\Rightarrow{t}=−\mathrm{1}\:\Rightarrow \\ $$ $${I}\:=\:−\int_{−\mathrm{1}} ^{\mathrm{1}\:} \sqrt{\frac{{b}−{a}}{\mathrm{2}}\left(\mathrm{1}+{t}\right)\frac{{b}−{a}}{\mathrm{2}}\left(\mathrm{1}−{t}\right)}\:\frac{{a}−{b}}{\mathrm{2}}{dt} \\ $$ $${I}=\frac{\left({b}−{a}\right)^{\mathrm{2}} }{\mathrm{4}}\:\int_{−\mathrm{1}} ^{\mathrm{1}} \:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} \:}\:{dt}=\:\frac{\left({b}−{a}\right)^{\mathrm{2}} }{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:{dt}\:{ch}.{t}={sin}\theta \\ $$ $${give}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} \:}\:{dt}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\theta\:{cos}\theta{d}\theta=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}} \theta\:{d}\theta \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\mathrm{1}+{cos}\left(\mathrm{2}\theta\right){d}\theta\:=\:\frac{\pi}{\mathrm{4}}\:\Rightarrow\:{I}=\:\frac{\left({b}−{a}\right)^{\mathrm{2}} }{\mathrm{8}}\:.{then}\:{let}\:{take}\right. \\ $$ $${a}=\mathrm{1}\:{and}\:{b}=\sqrt{\mathrm{2}}\:{we}\:{get} \\ $$ $$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \sqrt{\left(\sqrt{\mathrm{2}}\:−{x}\right)\left({x}−\mathrm{1}\right)}\:{dx}=\frac{\left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{8}}=\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{8}}\:. \\ $$ $$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com