
Question and Answers Forum
Question Number 31083 by abdo imad last updated on 02/Mar/18
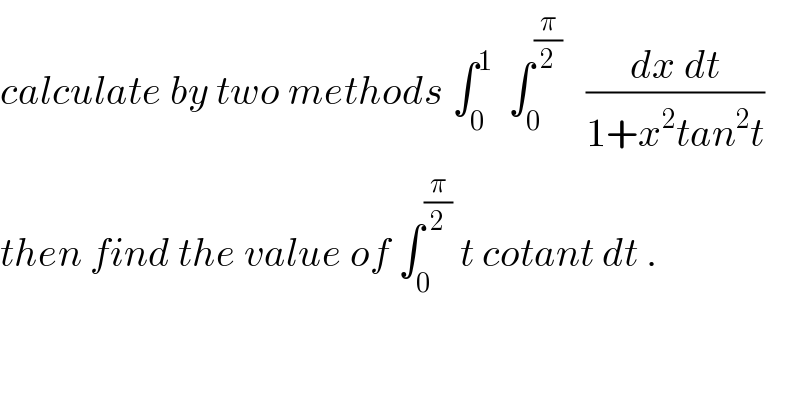
Commented by abdo imad last updated on 11/Mar/18
![let put I= ∫_0 ^(π/2) (∫_0 ^1 (dx/(1+x^2 tan^2 t)))dt ch. xtant=u give ∫_0 ^1 (dx/(1+x^2 tan^2 t))= ∫_0 ^1 (1/(1+u^2 )) (du/(tant)) =(1/(tant)) [arctanu]_0 ^(tant) = (t/(tant)) ⇒ I= ∫_0 ^(π/2) t cotant dt from another side by fubini theorem we have I= ∫_0 ^1 (∫_0 ^(π/2) (dt/(1+x^2 tan^2 t)))dx the ch.tant =u give ∫_0 ^(π/2) (dt/(1+x^2 tan^2 t)) = ∫_0 ^∞ (du/((1+u^2 )(1+x^2 u^2 ))) let decompose F(u)= (1/((1+u^2 )(1+x^2 u^2 ))) =((au+b)/(1+u^2 )) +((cu +d)/(1+x^2 u^2 )) F(−u)=F(u) ⇒((−au +b)/(1+u^2 )) +((−cu+d)/(1+x^2 u^2 ))=F(u) ⇒a=c=0⇒ F(u) =(b/(1+u^2 )) +(d/(1+x^2 u^2 )) lim_(u→∞) u^2 F(u)=0=b +(d/x^2 ) ⇒ d=−bx^2 ⇒F(u)= (b/(1+u^2 )) −((bx^2 )/(1+x^2 u^2 )) we look that b=(1/(1−x^2 )) and F(u)=(1/(1−x^2 ))( (1/(1+u^2 )) −(x^2 /(1+x^2 u^2 ))) ∫_0 ^∞ F(u)du= (1/(1−x^2 ))∫_0 ^∞ (du/(1+u^2 )) −(x^2 /(1−x^2 )) ∫_0 ^(+∞) (du/(1+x^2 u^2 )) =(π/(2(1−x^2 ))) −(x^2 /(1−x^2 )) ∫_0 ^∞ (1/(1+α^2 ))(dα/x) (ch.xu=α) = (π/(2(1−x^2 ))) −((πx)/(2(1−x^2 )))=((π(1−x))/(2(1−x)(1+x))) = (π/(2(1+x))) I =∫_0 ^1 ((πdx)/(2(1+x))) =(π/2) ∫_0 ^1 (dx/(1+x)) =(π/2) ln(2) ⇒ ∫_0 ^(π/2) t cotant dt =(π/2)ln(2).](Q31627.png)
| ||
Question and Answers Forum | ||
Question Number 31083 by abdo imad last updated on 02/Mar/18 | ||
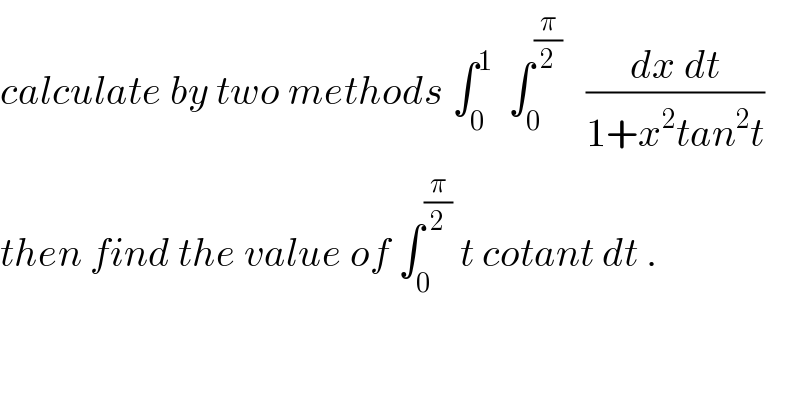 | ||
Commented by abdo imad last updated on 11/Mar/18 | ||
![let put I= ∫_0 ^(π/2) (∫_0 ^1 (dx/(1+x^2 tan^2 t)))dt ch. xtant=u give ∫_0 ^1 (dx/(1+x^2 tan^2 t))= ∫_0 ^1 (1/(1+u^2 )) (du/(tant)) =(1/(tant)) [arctanu]_0 ^(tant) = (t/(tant)) ⇒ I= ∫_0 ^(π/2) t cotant dt from another side by fubini theorem we have I= ∫_0 ^1 (∫_0 ^(π/2) (dt/(1+x^2 tan^2 t)))dx the ch.tant =u give ∫_0 ^(π/2) (dt/(1+x^2 tan^2 t)) = ∫_0 ^∞ (du/((1+u^2 )(1+x^2 u^2 ))) let decompose F(u)= (1/((1+u^2 )(1+x^2 u^2 ))) =((au+b)/(1+u^2 )) +((cu +d)/(1+x^2 u^2 )) F(−u)=F(u) ⇒((−au +b)/(1+u^2 )) +((−cu+d)/(1+x^2 u^2 ))=F(u) ⇒a=c=0⇒ F(u) =(b/(1+u^2 )) +(d/(1+x^2 u^2 )) lim_(u→∞) u^2 F(u)=0=b +(d/x^2 ) ⇒ d=−bx^2 ⇒F(u)= (b/(1+u^2 )) −((bx^2 )/(1+x^2 u^2 )) we look that b=(1/(1−x^2 )) and F(u)=(1/(1−x^2 ))( (1/(1+u^2 )) −(x^2 /(1+x^2 u^2 ))) ∫_0 ^∞ F(u)du= (1/(1−x^2 ))∫_0 ^∞ (du/(1+u^2 )) −(x^2 /(1−x^2 )) ∫_0 ^(+∞) (du/(1+x^2 u^2 )) =(π/(2(1−x^2 ))) −(x^2 /(1−x^2 )) ∫_0 ^∞ (1/(1+α^2 ))(dα/x) (ch.xu=α) = (π/(2(1−x^2 ))) −((πx)/(2(1−x^2 )))=((π(1−x))/(2(1−x)(1+x))) = (π/(2(1+x))) I =∫_0 ^1 ((πdx)/(2(1+x))) =(π/2) ∫_0 ^1 (dx/(1+x)) =(π/2) ln(2) ⇒ ∫_0 ^(π/2) t cotant dt =(π/2)ln(2).](Q31627.png) | ||