
Question and Answers Forum
Question Number 31085 by abdo imad last updated on 02/Mar/18
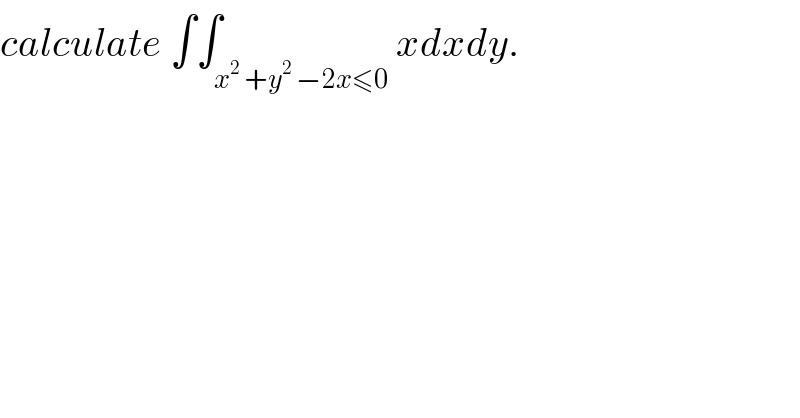
Commented by abdo imad last updated on 11/Mar/18
![let use the olar coordinates x=rcosθ and y=rsinθ x^2 +y^2 −2x ≤0 ⇔ r^2 −2rcosθ≤0 ⇔ 0<r≤2coθ due to diffeomorphisme ((−π)/2)≤θ≤(π/2) ⇒ I=∫∫_(−(π/2)≤θ≤(π/2) and 0<r≤2cosθ) rcosθ rdrdθ =∫_(−(π/2)) ^(π/2) ( ∫_0 ^(2cosθ) r^2 dr)cosθ dθ but ∫_0 ^(2cosθ) r^2 dr=[(1/3)r^3 ]_0 ^(2cosθ) =(8/3) cos^3 θ ⇒ I= (8/3) ∫_(−(π/2)) ^(π/2) cos^4 dθ =((16)/3) ∫_0 ^(π/2) (((1+cos(2θ))^2 )/4)dθ =(4/3)∫_0 ^(π/2) (1+2cos(2θ)+((1+cos(4θ))/2))dθ =(4/3)(π/2) +(8/3)∫_0 ^(π/2) cos(2θ)dθ +(2/3) (π/2) +(2/3) ∫_0 ^(π/2) cos(4θ)dθ =((2π)/3) +0 +(π/3) +0 =π ⇒ I=π.](Q31622.png)
| ||
Question and Answers Forum | ||
Question Number 31085 by abdo imad last updated on 02/Mar/18 | ||
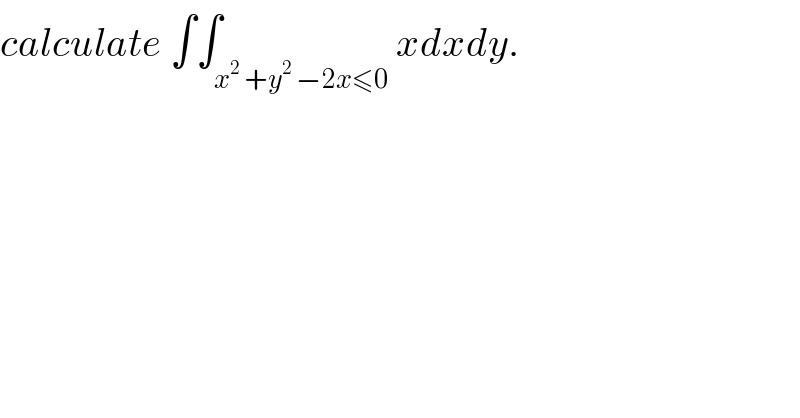 | ||
Commented by abdo imad last updated on 11/Mar/18 | ||
![let use the olar coordinates x=rcosθ and y=rsinθ x^2 +y^2 −2x ≤0 ⇔ r^2 −2rcosθ≤0 ⇔ 0<r≤2coθ due to diffeomorphisme ((−π)/2)≤θ≤(π/2) ⇒ I=∫∫_(−(π/2)≤θ≤(π/2) and 0<r≤2cosθ) rcosθ rdrdθ =∫_(−(π/2)) ^(π/2) ( ∫_0 ^(2cosθ) r^2 dr)cosθ dθ but ∫_0 ^(2cosθ) r^2 dr=[(1/3)r^3 ]_0 ^(2cosθ) =(8/3) cos^3 θ ⇒ I= (8/3) ∫_(−(π/2)) ^(π/2) cos^4 dθ =((16)/3) ∫_0 ^(π/2) (((1+cos(2θ))^2 )/4)dθ =(4/3)∫_0 ^(π/2) (1+2cos(2θ)+((1+cos(4θ))/2))dθ =(4/3)(π/2) +(8/3)∫_0 ^(π/2) cos(2θ)dθ +(2/3) (π/2) +(2/3) ∫_0 ^(π/2) cos(4θ)dθ =((2π)/3) +0 +(π/3) +0 =π ⇒ I=π.](Q31622.png) | ||