Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 31092 by abdo imad last updated on 02/Mar/18

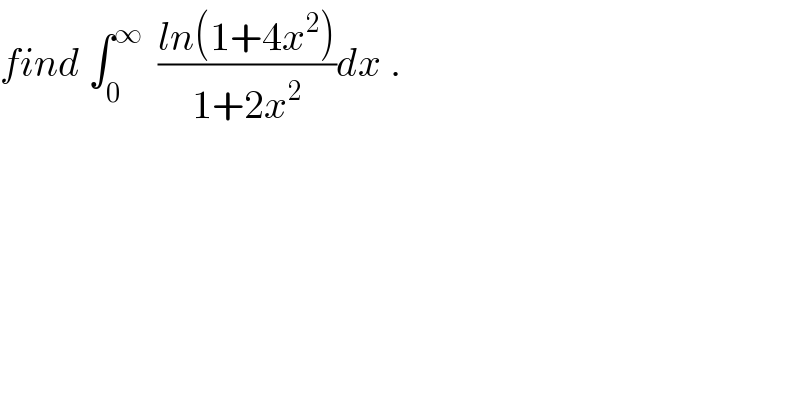
find ∫_0 ^∞ ((ln(1+4x^2 ))/(1+2x^2 ))dx .

$${find}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left(\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }{dx}\:. \\ $$

Commented by abdo imad last updated on 07/Mar/18

let introduce the parametric function f(t)=∫_0 ^∞ ((ln(1+tx^2 ))/(1+2x^2 ))dx with t≥0 wehave f^′ (t)=∫_0 ^∞ (x^2 /((1+tx^2 )(1+2x^2 )))dx =(1/2)∫_0 ^∞ ((2x^2 +1−1)/((1+tx^2 )(1+2x^2 )))dx=(1/2)∫_0 ^∞ (dx/(1+tx^2 )) −(1/2)∫_0 ^∞ (dx/((1+2x^2 )(1+tx^2 ))) but ∫_0 ^∞ (dx/(1+tx^2 )) =_((√t)x=u) =∫_0 ^∞ (1/(1+u^2 )) (du/(√t))=(π/(2(√t))) now let decompose F(t)= (1/((1+2x^2 )(1+tx^2 )))=((ax+b)/(2x^2 +1)) +((cx+d)/(tx^2 +1)) F(−x)=F(x)⇒F(x)=((−ax+b)/(2x^2 +1)) +((−cx +d)/(tx^2 +1))⇒a=c=0 ⇒ F(x)=(b/(2x^2 +1)) +(d/(t^ x^2 +1)) we have lim_(x→+∞) x^2 F(x)=0 =(b/2) +(d/t)=0⇒2d +tb=0 ⇒d=−(t/2)b⇒ F(t)= (b/(2x^2 +1)) −(t/2) (b/(tx^2 +1)) wehave F(0)=1=b −((tb)/2) ⇒ (1−(t/2))b=1 ⇒ (2−t)b=2 ⇒b= (2/(2−t)) ⇒ F(x)= (2/((2−t)(2x^2 +1))) − (t/((2−t)(tx^2 +1))) =(1/(2−t))( (2/(2x^2 +1)) −(t/(tx^2 +1)))⇒ ∫_0 ^∞ F(x)dx= (2/(2−t))∫_0 ^∞ (dx/(2x^2 +1)) −(t/(2−t))∫_0 ^∞ (dx/(tx^2 +1)) but ∫_0 ^∞ (dx/(2x^2 +1))=_((√2)x=u) ∫_0 ^∞ (1/(1+u^2 )) (du/(√2))=(π/(2(√2))). ∫_0 ^∞ (dx/(tx^2 +1))=(π/(2(√t))) ⇒∫_0 ^∞ F(x)dx= (π/((√2)(2−t))) −(t/(2−t)) (π/(2(√t))) =(π/((√2)(2−t))) −((π(√t))/(2(2−t))) ⇒f^′ (t)=(π/(4(√t))) −(π/(2(√2)(2−t))) +((π(√t))/(4(2−t))) =(π/4)( (1/(√t)) −((2π)/((√2)(2−t))) +((√t)/(2−t)))⇒ f(t)=(π/4)∫ (dt/(√t)) −(π/(2(√2)))∫ (dt/(2−t)) +(π/4)∫ ((√t)/(2−t))dt +λ =(π/2)(√t) +(π/(2(√2)))ln∣2−t∣ +(π/4)∫ (u/(2−u^2 )) 2udu +λ (π/4)∫ ((2u^2 )/(2−u^2 ))du=(π/2) ∫ (u^2 /(2−u^2 ))du and ∫ (u^2 /(2−u^2 ))du= −∫ ((2−u^2 −2)/(2−u^2 ))du=−u +2∫ (du/(2−u^2 )) =−u +(1/(√2)) ∫( (1/((√2) −u)) +(1/((√2) +u)))=−(√t) +(1/(√2))ln∣(((√2) +(√t))/((√2) −(√t)))∣ ⇒ f(t)=(π/2)(√t) +(π/(2(√2)))ln∣2−t∣ +(π/2)(−(√t) +(1/(√2))ln∣(((√2) +(√t))/((√2) −(√t)))∣)+λ f(t)=(π/(2(√2)))ln∣2−t∣ +(π/(2(√2)))ln∣(((√2) +(√t))/((√2) −(√t)))∣ +λ we have f(0)=0=((πln2)/(2(√2))) +λ ⇒λ=−((πln2)/(2(√2))) finally f(t)=(π/(2(√2)))ln∣2−t∣ +(π/(2(√2)))ln∣(((√2) +(√t))/((√2) −(√t)))∣ −((πln2)/(2(√2))) let take t=4 ∫_0 ^∞ ((ln(1+4t^2 ))/(1+2t^2 ))=(π/(2(√2)))ln2 +(π/(2(√2)))ln∣(((√2) +2)/((√2) −2))∣ −((πln2)/(2(√2))) .

$${let}\:{introduce}\:{the}\:{parametric}\:{function} \\ $$$${f}\left({t}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left(\mathrm{1}+{tx}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }{dx}\:{with}\:{t}\geqslant\mathrm{0}\:{wehave} \\ $$$${f}^{'} \left({t}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{tx}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} \right)}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{\left(\mathrm{1}+{tx}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} \right)}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\mathrm{1}+{tx}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left(\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{tx}^{\mathrm{2}} \right)}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\mathrm{1}+{tx}^{\mathrm{2}} }\:=_{\sqrt{{t}}{x}={u}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{{du}}{\sqrt{{t}}}=\frac{\pi}{\mathrm{2}\sqrt{{t}}}\:\:{now}\:{let}\:{decompose} \\ $$$${F}\left({t}\right)=\:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{tx}^{\mathrm{2}} \right)}=\frac{{ax}+{b}}{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{cx}+{d}}{{tx}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(−{x}\right)={F}\left({x}\right)\Rightarrow{F}\left({x}\right)=\frac{−{ax}+{b}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}\:+\frac{−{cx}\:+{d}}{{tx}^{\mathrm{2}} +\mathrm{1}}\Rightarrow{a}={c}=\mathrm{0}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{{b}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}\:+\frac{{d}}{{t}^{} {x}^{\mathrm{2}} +\mathrm{1}}\:{we}\:{have}\:{lim}_{{x}\rightarrow+\infty} {x}^{\mathrm{2}} {F}\left({x}\right)=\mathrm{0} \\ $$$$=\frac{{b}}{\mathrm{2}}\:+\frac{{d}}{{t}}=\mathrm{0}\Rightarrow\mathrm{2}{d}\:+{tb}=\mathrm{0}\:\Rightarrow{d}=−\frac{{t}}{\mathrm{2}}{b}\Rightarrow \\ $$$${F}\left({t}\right)=\:\frac{{b}}{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}\:−\frac{{t}}{\mathrm{2}}\:\frac{{b}}{{tx}^{\mathrm{2}} +\mathrm{1}}\:\:{wehave}\:{F}\left(\mathrm{0}\right)=\mathrm{1}={b}\:−\frac{{tb}}{\mathrm{2}}\:\Rightarrow \\ $$$$\left(\mathrm{1}−\frac{{t}}{\mathrm{2}}\right){b}=\mathrm{1}\:\Rightarrow\:\left(\mathrm{2}−{t}\right){b}=\mathrm{2}\:\Rightarrow{b}=\:\frac{\mathrm{2}}{\mathrm{2}−{t}}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\:\frac{\mathrm{2}}{\left(\mathrm{2}−{t}\right)\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)}\:−\:\:\frac{{t}}{\left(\mathrm{2}−{t}\right)\left({tx}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}−{t}}\left(\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}\:−\frac{{t}}{{tx}^{\mathrm{2}} \:+\mathrm{1}}\right)\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{F}\left({x}\right){dx}=\:\frac{\mathrm{2}}{\mathrm{2}−{t}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}\:−\frac{{t}}{\mathrm{2}−{t}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{{tx}^{\mathrm{2}} +\mathrm{1}}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}=_{\sqrt{\mathrm{2}}{x}={u}} \:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{{du}}{\sqrt{\mathrm{2}}}=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}. \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{{tx}^{\mathrm{2}} \:+\mathrm{1}}=\frac{\pi}{\mathrm{2}\sqrt{{t}}}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} {F}\left({x}\right){dx}=\:\frac{\pi}{\sqrt{\mathrm{2}}\left(\mathrm{2}−{t}\right)}\:−\frac{{t}}{\mathrm{2}−{t}}\:\frac{\pi}{\mathrm{2}\sqrt{{t}}} \\ $$$$=\frac{\pi}{\sqrt{\mathrm{2}}\left(\mathrm{2}−{t}\right)}\:−\frac{\pi\sqrt{{t}}}{\mathrm{2}\left(\mathrm{2}−{t}\right)}\:\Rightarrow{f}^{'} \left({t}\right)=\frac{\pi}{\mathrm{4}\sqrt{{t}}}\:−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}\left(\mathrm{2}−{t}\right)}\:+\frac{\pi\sqrt{{t}}}{\mathrm{4}\left(\mathrm{2}−{t}\right)} \\ $$$$=\frac{\pi}{\mathrm{4}}\left(\:\:\:\frac{\mathrm{1}}{\sqrt{{t}}}\:−\frac{\mathrm{2}\pi}{\sqrt{\mathrm{2}}\left(\mathrm{2}−{t}\right)}\:+\frac{\sqrt{{t}}}{\mathrm{2}−{t}}\right)\Rightarrow \\ $$$${f}\left({t}\right)=\frac{\pi}{\mathrm{4}}\int\:\frac{{dt}}{\sqrt{{t}}}\:−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\int\:\:\frac{{dt}}{\mathrm{2}−{t}}\:+\frac{\pi}{\mathrm{4}}\int\:\:\frac{\sqrt{{t}}}{\mathrm{2}−{t}}{dt}\:+\lambda \\ $$$$=\frac{\pi}{\mathrm{2}}\sqrt{{t}}\:\:+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid\mathrm{2}−{t}\mid\:+\frac{\pi}{\mathrm{4}}\int\:\:\:\:\frac{{u}}{\mathrm{2}−{u}^{\mathrm{2}} }\:\mathrm{2}{udu}\:+\lambda \\ $$$$\frac{\pi}{\mathrm{4}}\int\:\:\:\frac{\mathrm{2}{u}^{\mathrm{2}} }{\mathrm{2}−{u}^{\mathrm{2}} }{du}=\frac{\pi}{\mathrm{2}}\:\int\:\frac{{u}^{\mathrm{2}} }{\mathrm{2}−{u}^{\mathrm{2}} }{du}\:{and} \\ $$$$\int\:\:\frac{{u}^{\mathrm{2}} }{\mathrm{2}−{u}^{\mathrm{2}} }{du}=\:−\int\:\:\frac{\mathrm{2}−{u}^{\mathrm{2}} \:−\mathrm{2}}{\mathrm{2}−\boldsymbol{{u}}^{\mathrm{2}} }\boldsymbol{{du}}=−\boldsymbol{{u}}\:\:+\mathrm{2}\int\:\:\:\frac{{du}}{\mathrm{2}−{u}^{\mathrm{2}} } \\ $$$$=−{u}\:\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\int\left(\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}}\:−{u}}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}\:+{u}}\right)=−\sqrt{{t}}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{ln}\mid\frac{\sqrt{\mathrm{2}}\:+\sqrt{{t}}}{\sqrt{\mathrm{2}}\:−\sqrt{{t}}}\mid\:\Rightarrow \\ $$$${f}\left({t}\right)=\frac{\pi}{\mathrm{2}}\sqrt{{t}}\:\:+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid\mathrm{2}−{t}\mid\:+\frac{\pi}{\mathrm{2}}\left(−\sqrt{{t}}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{ln}\mid\frac{\sqrt{\mathrm{2}}\:+\sqrt{{t}}}{\sqrt{\mathrm{2}}\:−\sqrt{{t}}}\mid\right)+\lambda \\ $$$${f}\left({t}\right)=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid\mathrm{2}−{t}\mid\:+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid\frac{\sqrt{\mathrm{2}}\:+\sqrt{{t}}}{\sqrt{\mathrm{2}}\:−\sqrt{{t}}}\mid\:+\lambda\:{we}\:{have} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}=\frac{\pi{ln}\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}}\:+\lambda\:\Rightarrow\lambda=−\frac{\pi{ln}\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}}\:{finally} \\ $$$${f}\left({t}\right)=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid\mathrm{2}−{t}\mid\:+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid\frac{\sqrt{\mathrm{2}}\:+\sqrt{{t}}}{\sqrt{\mathrm{2}}\:−\sqrt{{t}}}\mid\:−\frac{\pi{ln}\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}}\:{let}\:{take}\:{t}=\mathrm{4} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left(\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{2}{t}^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mathrm{2}\:+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid\frac{\sqrt{\mathrm{2}}\:+\mathrm{2}}{\sqrt{\mathrm{2}}\:−\mathrm{2}}\mid\:−\frac{\pi{ln}\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com