
Question and Answers Forum
Question Number 31105 by abdo imad last updated on 02/Mar/18
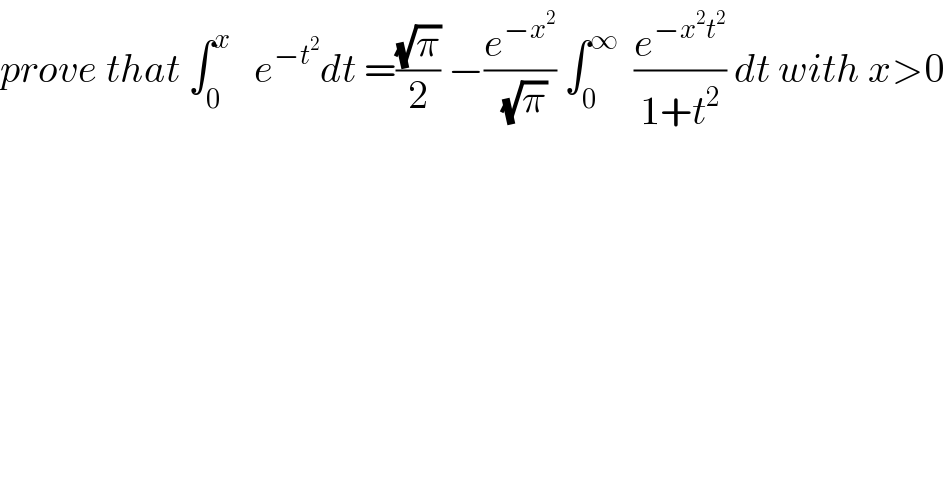
Commented byabdo imad last updated on 05/Mar/18
![let put f(x)= ∫_0 ^∞ (e^(−x^2 t^2 ) /(1+t^2 ))dt with x>0 after verifying the conditions of derivality of f on ]0,+∞[ we get f^′ (x)= −∫_0 ^∞ ((2t^2 x e^(−x^2 t^2 ) )/(1+t^2 ))dt= −2x ∫_0 ^∞ ((t^2 e^(−x^2 t^2 ) )/(1+t^2 ))dt =−2x∫_0 ^∞ (((1+t^2 −1)e^(−x^2 t^2 ) )/(1+t^2 ))dt=−2x ∫_0 ^∞ e^(−x^2 t^2 ) dt +2x∫_0 ^∞ (e^(−x^2 t^2 ) /(1+t^2 ))dt =2x f(x)−2x ∫_0 ^∞ e^(−(xt)^2 ) dt=2xf(x)−2x ∫_0 ^∞ e^(−u^2 ) (du/x) =2xf(x)−(√π) ⇒ f^′ (x) −2xf(x)=−(√π) e.h⇒f^′ −2xf=0⇒(f^′ /f)=2x⇒ln∣f∣= x^2 ⇒f(x)=k e^x^2 mvc method⇒k^′ e^x^2 + 2kx e^x^2 −2xk e^x^2 =−(√π) ⇒ k^′ e^x^2 =−(√π) ⇒k^′ =−(√π) e^(−x^2 ) ⇒k(x)= ∫_0 ^x −(√π) e^(−t^2 ) dt +λ λ=k(0)=f(0)=(π/2) ⇒k(x)=(π/2) −(√π) ∫_0 ^x e^(−t^2 ) dt ⇒ ∫_0 ^∞ (e^(−x^2 t^2 ) /(1+t^2 ))dt=((π/2) −(√π) ∫_0 ^x e^(−t^2 ) dt)e^x^2 ⇒ e^(−x^2 ) ∫_0 ^∞ (e^(−x^2 t^2 ) /(1+t^2 ))dt= (π/2) −(√π) ∫_0 ^x e^(−t^2 ) dt ⇒ (√π) ∫_0 ^x e^(−t^2 ) dt= (π/2) − e^(−x^2 ) ∫_0 ^∞ (e^(−x^2 t^2 ) /(1+t^2 ))dt ⇒ ∫_0 ^x e^(−t^2 ) dt= ((√π)/2) −(e^(−x^2 ) /(√π)) ∫_0 ^∞ (e^(−x^2 t^2 ) /(1+t^2 ))dt .](Q31297.png)
| ||
Question and Answers Forum | ||
Question Number 31105 by abdo imad last updated on 02/Mar/18 | ||
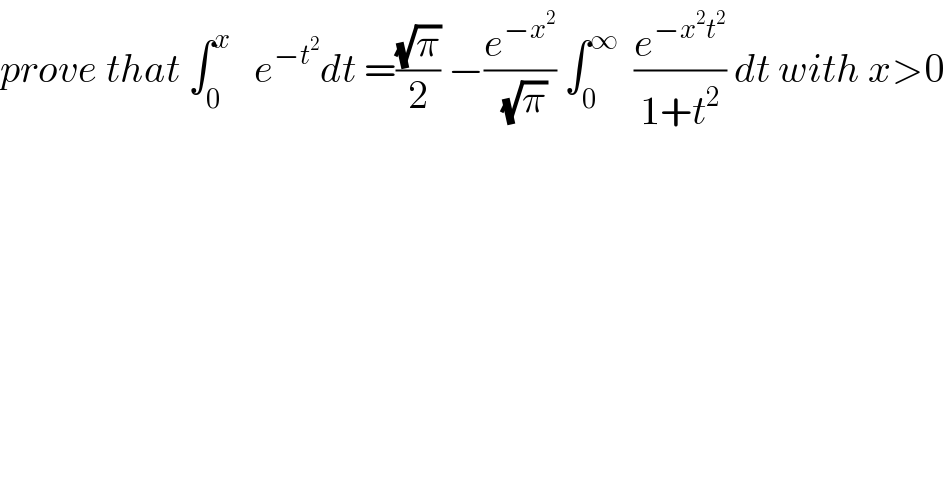 | ||
Commented byabdo imad last updated on 05/Mar/18 | ||
![let put f(x)= ∫_0 ^∞ (e^(−x^2 t^2 ) /(1+t^2 ))dt with x>0 after verifying the conditions of derivality of f on ]0,+∞[ we get f^′ (x)= −∫_0 ^∞ ((2t^2 x e^(−x^2 t^2 ) )/(1+t^2 ))dt= −2x ∫_0 ^∞ ((t^2 e^(−x^2 t^2 ) )/(1+t^2 ))dt =−2x∫_0 ^∞ (((1+t^2 −1)e^(−x^2 t^2 ) )/(1+t^2 ))dt=−2x ∫_0 ^∞ e^(−x^2 t^2 ) dt +2x∫_0 ^∞ (e^(−x^2 t^2 ) /(1+t^2 ))dt =2x f(x)−2x ∫_0 ^∞ e^(−(xt)^2 ) dt=2xf(x)−2x ∫_0 ^∞ e^(−u^2 ) (du/x) =2xf(x)−(√π) ⇒ f^′ (x) −2xf(x)=−(√π) e.h⇒f^′ −2xf=0⇒(f^′ /f)=2x⇒ln∣f∣= x^2 ⇒f(x)=k e^x^2 mvc method⇒k^′ e^x^2 + 2kx e^x^2 −2xk e^x^2 =−(√π) ⇒ k^′ e^x^2 =−(√π) ⇒k^′ =−(√π) e^(−x^2 ) ⇒k(x)= ∫_0 ^x −(√π) e^(−t^2 ) dt +λ λ=k(0)=f(0)=(π/2) ⇒k(x)=(π/2) −(√π) ∫_0 ^x e^(−t^2 ) dt ⇒ ∫_0 ^∞ (e^(−x^2 t^2 ) /(1+t^2 ))dt=((π/2) −(√π) ∫_0 ^x e^(−t^2 ) dt)e^x^2 ⇒ e^(−x^2 ) ∫_0 ^∞ (e^(−x^2 t^2 ) /(1+t^2 ))dt= (π/2) −(√π) ∫_0 ^x e^(−t^2 ) dt ⇒ (√π) ∫_0 ^x e^(−t^2 ) dt= (π/2) − e^(−x^2 ) ∫_0 ^∞ (e^(−x^2 t^2 ) /(1+t^2 ))dt ⇒ ∫_0 ^x e^(−t^2 ) dt= ((√π)/2) −(e^(−x^2 ) /(√π)) ∫_0 ^∞ (e^(−x^2 t^2 ) /(1+t^2 ))dt .](Q31297.png) | ||