Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 31296 by abdo imad last updated on 05/Mar/18

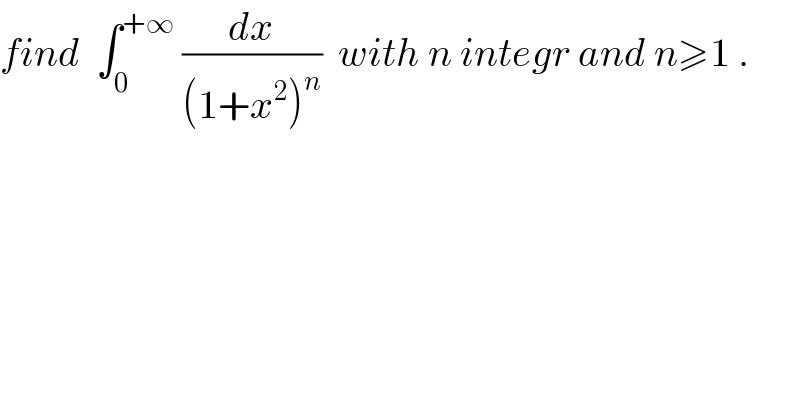
find ∫_0 ^(+∞) (dx/((1+x^2 )^n )) with n integr and n≥1 .

$${find}\:\:\int_{\mathrm{0}} ^{+\infty} \:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{{n}} }\:\:{with}\:{n}\:{integr}\:{and}\:{n}\geqslant\mathrm{1}\:. \\ $$

Commented by NECx last updated on 07/Mar/18

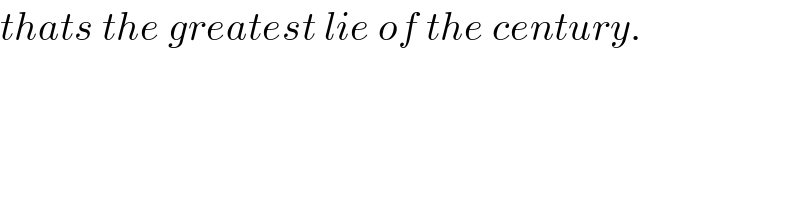
thats the greatest lie of the century.

$${thats}\:{the}\:{greatest}\:{lie}\:{of}\:{the}\:{century}. \\ $$

Commented by abdo imad last updated on 06/Mar/18

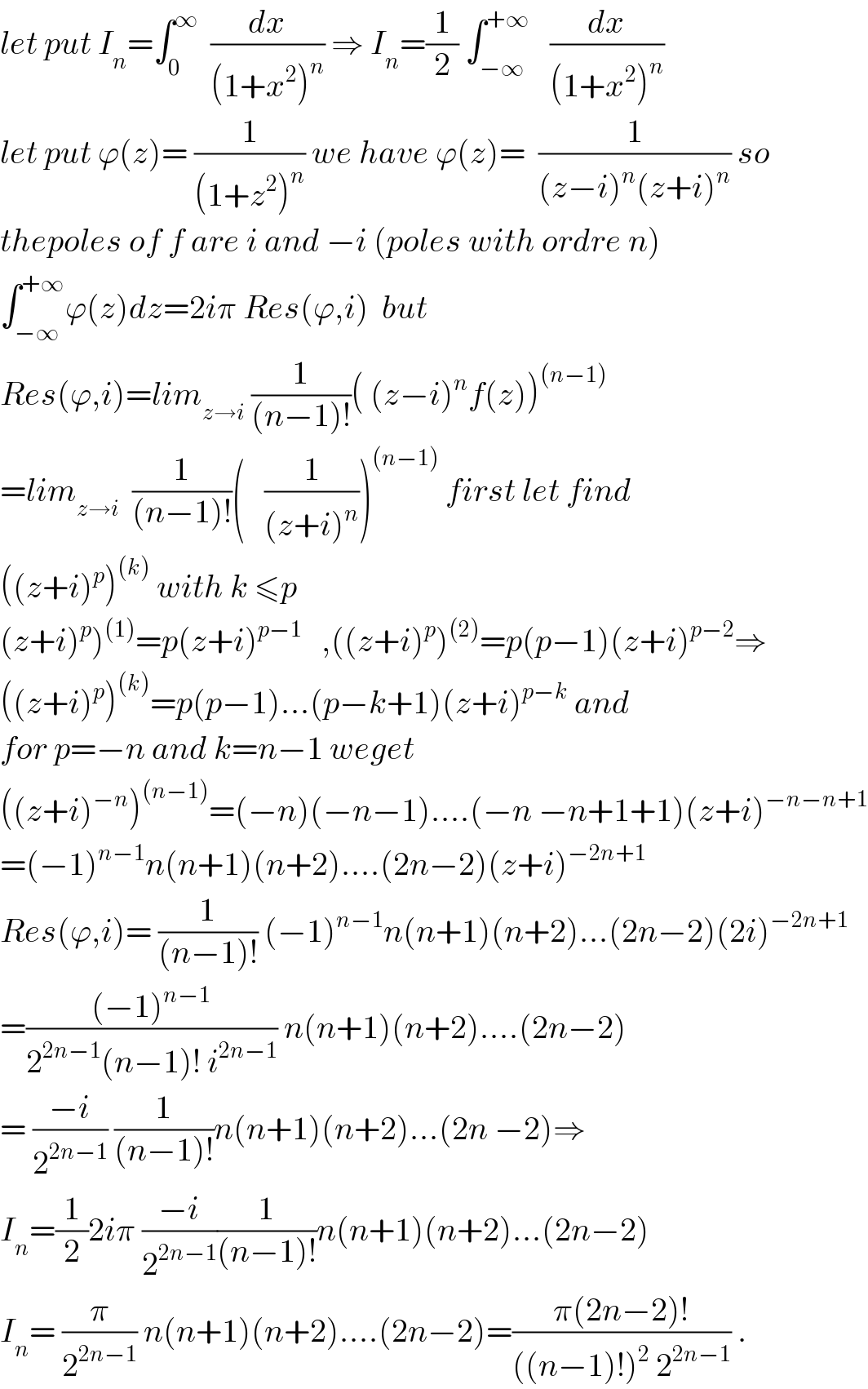
let put I_n =∫_0 ^∞ (dx/((1+x^2 )^n )) ⇒ I_n =(1/2) ∫_(−∞) ^(+∞) (dx/((1+x^2 )^n )) let put ϕ(z)= (1/((1+z^2 )^n )) we have ϕ(z)= (1/((z−i)^n (z+i)^n )) so thepoles of f are i and −i (poles with ordre n) ∫_(−∞) ^(+∞) ϕ(z)dz=2iπ Res(ϕ,i) but Res(ϕ,i)=lim_(z→i) (1/((n−1)!))( (z−i)^n f(z))^((n−1)) =lim_(z→i) (1/((n−1)!))( (1/((z+i)^n )))^((n−1)) first let find ((z+i)^p )^((k)) with k ≤p (z+i)^p )^((1)) =p(z+i)^(p−1) ,((z+i)^p )^((2)) =p(p−1)(z+i)^(p−2) ⇒ ((z+i)^p )^((k)) =p(p−1)...(p−k+1)(z+i)^(p−k) and for p=−n and k=n−1 weget ((z+i)^(−n) )^((n−1)) =(−n)(−n−1)....(−n −n+1+1)(z+i)^(−n−n+1) =(−1)^(n−1) n(n+1)(n+2)....(2n−2)(z+i)^(−2n+1) Res(ϕ,i)= (1/((n−1)!)) (−1)^(n−1) n(n+1)(n+2)...(2n−2)(2i)^(−2n+1) =(((−1)^(n−1) )/(2^(2n−1) (n−1)! i^(2n−1) )) n(n+1)(n+2)....(2n−2) = ((−i)/2^(2n−1) ) (1/((n−1)!))n(n+1)(n+2)...(2n −2)⇒ I_n =(1/2)2iπ ((−i)/2^(2n−1) )(1/((n−1)!))n(n+1)(n+2)...(2n−2) I_n = (π/2^(2n−1) ) n(n+1)(n+2)....(2n−2)=((π(2n−2)!)/(((n−1)!)^2 2^(2n−1) )) .

$${let}\:{put}\:{I}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{{n}} }\:\Rightarrow\:{I}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{{n}} }\: \\ $$$${let}\:{put}\:\varphi\left({z}\right)=\:\frac{\mathrm{1}}{\left(\mathrm{1}+{z}^{\mathrm{2}} \right)^{{n}} }\:{we}\:{have}\:\varphi\left({z}\right)=\:\:\frac{\mathrm{1}}{\left({z}−{i}\right)^{{n}} \left({z}+{i}\right)^{{n}} }\:{so} \\ $$$${thepoles}\:{of}\:{f}\:{are}\:{i}\:{and}\:−{i}\:\left({poles}\:{with}\:{ordre}\:{n}\right) \\ $$$$\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{i}\right)\:\:{but} \\ $$$${Res}\left(\varphi,{i}\right)={lim}_{{z}\rightarrow{i}} \:\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}\left(\:\left({z}−{i}\right)^{{n}} {f}\left({z}\right)\right)^{\left({n}−\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{i}} \:\:\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}\left(\:\:\:\frac{\mathrm{1}}{\left({z}+{i}\right)^{{n}} }\right)^{\left({n}−\mathrm{1}\right)} \:{first}\:{let}\:{find} \\ $$$$\left(\left({z}+{i}\right)^{{p}} \right)^{\left({k}\right)} \:{with}\:{k}\:\leqslant{p} \\ $$$$\left.\left({z}+{i}\right)^{{p}} \right)^{\left(\mathrm{1}\right)} ={p}\left({z}+{i}\right)^{{p}−\mathrm{1}} \:\:\:,\left(\left({z}+{i}\right)^{{p}} \right)^{\left(\mathrm{2}\right)} ={p}\left({p}−\mathrm{1}\right)\left({z}+{i}\right)^{{p}−\mathrm{2}} \Rightarrow \\ $$$$\left(\left({z}+{i}\right)^{{p}} \right)^{\left({k}\right)} ={p}\left({p}−\mathrm{1}\right)...\left({p}−{k}+\mathrm{1}\right)\left({z}+{i}\right)^{{p}−{k}} \:{and} \\ $$$${for}\:{p}=−{n}\:{and}\:{k}={n}−\mathrm{1}\:{weget} \\ $$$$\left(\left({z}+{i}\right)^{−{n}} \right)^{\left({n}−\mathrm{1}\right)} =\left(−{n}\right)\left(−{n}−\mathrm{1}\right)....\left(−{n}\:−{n}+\mathrm{1}+\mathrm{1}\right)\left({z}+{i}\right)^{−{n}−{n}+\mathrm{1}} \\ $$$$=\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)....\left(\mathrm{2}{n}−\mathrm{2}\right)\left({z}+{i}\right)^{−\mathrm{2}{n}+\mathrm{1}} \\ $$$${Res}\left(\varphi,{i}\right)=\:\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}\:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)...\left(\mathrm{2}{n}−\mathrm{2}\right)\left(\mathrm{2}{i}\right)^{−\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\:{i}^{\mathrm{2}{n}−\mathrm{1}} }\:{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)....\left(\mathrm{2}{n}−\mathrm{2}\right) \\ $$$$=\:\frac{−{i}}{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }\:\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)...\left(\mathrm{2}{n}\:−\mathrm{2}\right)\Rightarrow \\ $$$${I}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{2}{i}\pi\:\frac{−{i}}{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)...\left(\mathrm{2}{n}−\mathrm{2}\right) \\ $$$${I}_{{n}} =\:\frac{\pi}{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }\:{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)....\left(\mathrm{2}{n}−\mathrm{2}\right)=\frac{\pi\left(\mathrm{2}{n}−\mathrm{2}\right)!}{\left(\left({n}−\mathrm{1}\right)!\right)^{\mathrm{2}} \:\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }\:. \\ $$

Commented by NECx last updated on 07/Mar/18

wow..... Prof Abdo Imad,I′m so amased by the questions you solve.Thanks for you help on the platform.

$${wow}.....\:{Prof}\:{Abdo}\:{Imad},{I}'{m}\:{so} \\ $$$${amased}\:{by}\:{the}\:{questions}\:{you} \\ $$$${solve}.{Thanks}\:{for}\:{you}\:{help}\:{on}\:{the} \\ $$$${platform}. \\ $$

Commented by NECx last updated on 07/Mar/18

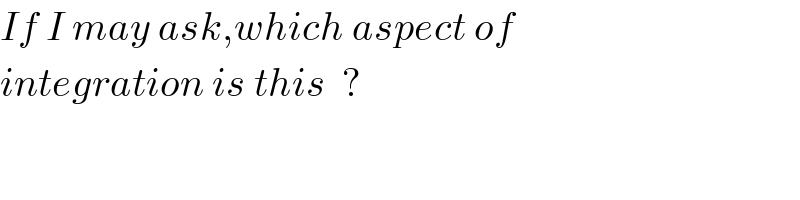
If I may ask,which aspect of integration is this ?

$${If}\:{I}\:{may}\:{ask},{which}\:{aspect}\:{of} \\ $$$${integration}\:{is}\:{this}\:\:? \\ $$

Commented by NECx last updated on 07/Mar/18

this is because I always notice that you always apply complex values to your integrals.

$${this}\:{is}\:{because}\:{I}\:{always}\:{notice} \\ $$$${that}\:{you}\:{always}\:{apply}\:{complex} \\ $$$${values}\:{to}\:{your}\:{integrals}. \\ $$

Commented by prof Abdo imad last updated on 07/Mar/18

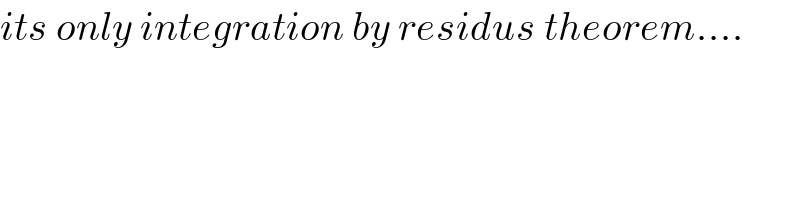
its only integration by residus theorem....

$${its}\:{only}\:{integration}\:{by}\:{residus}\:{theorem}.... \\ $$

Commented by prof Abdo imad last updated on 07/Mar/18

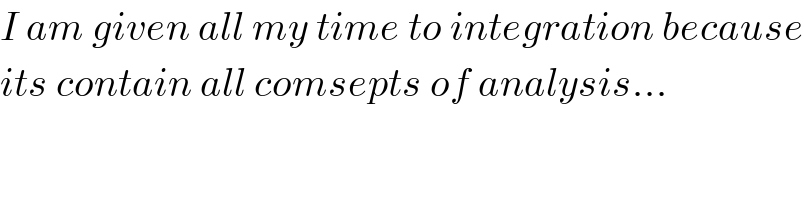
I am given all my time to integration because its contain all comsepts of analysis...

$${I}\:{am}\:{given}\:{all}\:{my}\:{time}\:{to}\:{integration}\:{because} \\ $$$${its}\:{contain}\:{all}\:{comsepts}\:{of}\:{analysis}... \\ $$

Commented by NECx last updated on 07/Mar/18

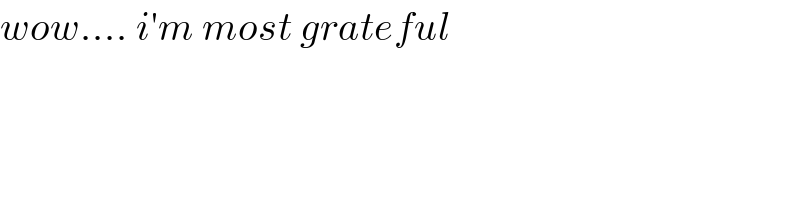
wow.... i′m most grateful

$${wow}....\:{i}'{m}\:{most}\:{grateful} \\ $$

Commented by NECx last updated on 07/Mar/18

I′ve heard of the theorem : cauchy residue theorem.It has to do with comlex analysis.Though its not in Class XI or XII syllabus.u

$${I}'{ve}\:{heard}\:{of}\:{the}\:{theorem}\::\:{cauchy} \\ $$$${residue}\:{theorem}.{It}\:{has}\:{to}\:{do}\:{with} \\ $$$${comlex}\:{analysis}.{Though}\:{its}\:{not} \\ $$$${in}\:{Class}\:{XI}\:{or}\:{XII}\:{syllabus}.{u} \\ $$

Commented by rahul 19 last updated on 07/Mar/18

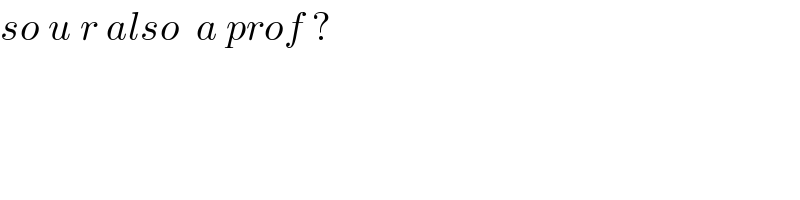
so u r also a prof ?

$${so}\:{u}\:{r}\:{also}\:\:{a}\:{prof}\:? \\ $$

Commented by rahul 19 last updated on 07/Mar/18

then?

$${then}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com