Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 3138 by prakash jain last updated on 05/Dec/15

Prove or disprove that S=Σ_(n=1) ^∞ (1/n^k ) , k∈Z^+ , k>1 is irrational.

$$\mathrm{Prove}\:\mathrm{or}\:\mathrm{disprove}\:\mathrm{that} \\ $$ $$\mathrm{S}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{{k}} }\:,\:{k}\in\mathbb{Z}^{+} ,\:{k}>\mathrm{1}\:\mathrm{is}\:\mathrm{irrational}. \\ $$

Commented by123456 last updated on 05/Dec/15

ζ(k) ζ(2)=(π^2 /6) wich is a rational multiple of π^2 , so its irational and in general ζ(2n)=qπ^(2n) q∈Q,n∈Z^+ so its irrational however nothing is know about ζ(2n+1) but also ζ(3)=ζ_3 is irrational (apery constant)

$$\zeta\left({k}\right) \\ $$ $$\zeta\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:\mathrm{wich}\:\mathrm{is}\:\mathrm{a}\:\mathrm{rational}\:\mathrm{multiple}\:\mathrm{of} \\ $$ $$\pi^{\mathrm{2}} ,\:\mathrm{so}\:\mathrm{its}\:\mathrm{irational} \\ $$ $$\mathrm{and}\:\mathrm{in}\:\mathrm{general} \\ $$ $$\zeta\left(\mathrm{2}{n}\right)={q}\pi^{\mathrm{2}{n}} \:{q}\in\mathbb{Q},{n}\in\mathbb{Z}^{+} \:\mathrm{so}\:\mathrm{its}\:\mathrm{irrational} \\ $$ $$\mathrm{however}\:\mathrm{nothing}\:\mathrm{is}\:\mathrm{know}\:\mathrm{about} \\ $$ $$\zeta\left(\mathrm{2}{n}+\mathrm{1}\right) \\ $$ $$\mathrm{but}\:\mathrm{also} \\ $$ $$\zeta\left(\mathrm{3}\right)=\zeta_{\mathrm{3}} \:\mathrm{is}\:\mathrm{irrational}\:\left(\mathrm{apery}\:\mathrm{constant}\right) \\ $$

Commented byFilup last updated on 06/Dec/15

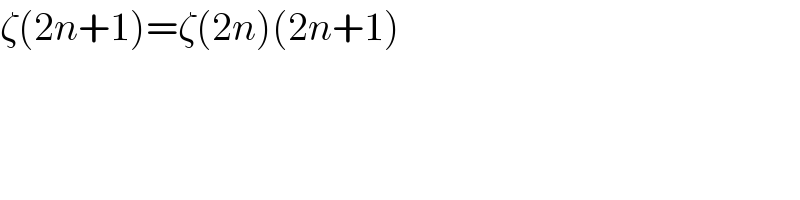
ζ(2n+1)=ζ(2n)(2n+1)

$$\zeta\left(\mathrm{2}{n}+\mathrm{1}\right)=\zeta\left(\mathrm{2}{n}\right)\left(\mathrm{2}{n}+\mathrm{1}\right) \\ $$

Commented byprakash jain last updated on 06/Dec/15

How did you come up with ζ(2n+1)=(2n+1)ζ(2n) ? From what i know read so far Funtional Equation ζ(s)=2^s π^(s−1) sin (((πs)/2))Γ(1−s)ζ(1−s) For s=−2n ζ(−2n)=0 s=+2n sin (((πs)/2))Γ(1−s) ≠0 so RHS ≠0

$$\mathrm{How}\:\mathrm{did}\:\mathrm{you}\:\mathrm{come}\:\mathrm{up}\:\mathrm{with} \\ $$ $$\zeta\left(\mathrm{2}{n}+\mathrm{1}\right)=\left(\mathrm{2}{n}+\mathrm{1}\right)\zeta\left(\mathrm{2}{n}\right)\:? \\ $$ $$\mathrm{From}\:\mathrm{what}\:\mathrm{i}\:\mathrm{know}\:\mathrm{read}\:\mathrm{so}\:\mathrm{far} \\ $$ $$\mathrm{Funtional}\:\mathrm{Equation} \\ $$ $$\zeta\left({s}\right)=\mathrm{2}^{{s}} \pi^{{s}−\mathrm{1}} \mathrm{sin}\:\left(\frac{\pi{s}}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}−{s}\right)\zeta\left(\mathrm{1}−{s}\right) \\ $$ $$\mathrm{For}\:{s}=−\mathrm{2}{n}\: \\ $$ $$\zeta\left(−\mathrm{2}{n}\right)=\mathrm{0} \\ $$ $${s}=+\mathrm{2}{n} \\ $$ $$\mathrm{sin}\:\left(\frac{\pi{s}}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}−{s}\right)\:\neq\mathrm{0}\:\mathrm{so}\:\mathrm{RHS}\:\neq\mathrm{0} \\ $$

Commented byFilup last updated on 06/Dec/15

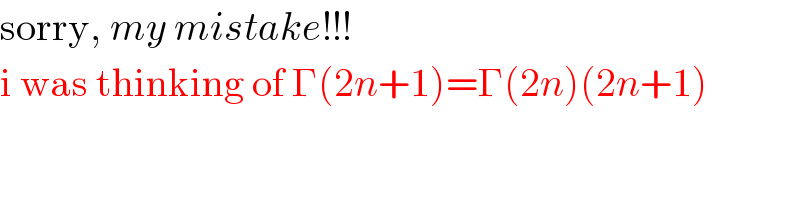
sorry, my mistake!!! i was thinking of Γ(2n+1)=Γ(2n)(2n+1)

$$\mathrm{sorry},\:{my}\:{mistake}!!! \\ $$ $$\mathrm{i}\:\mathrm{was}\:\mathrm{thinking}\:\mathrm{of}\:\Gamma\left(\mathrm{2}{n}+\mathrm{1}\right)=\Gamma\left(\mathrm{2}{n}\right)\left(\mathrm{2}{n}+\mathrm{1}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com