
Previous in Relation and Functions Next in Relation and Functions
Question Number 31422 by abdo imad last updated on 08/Mar/18
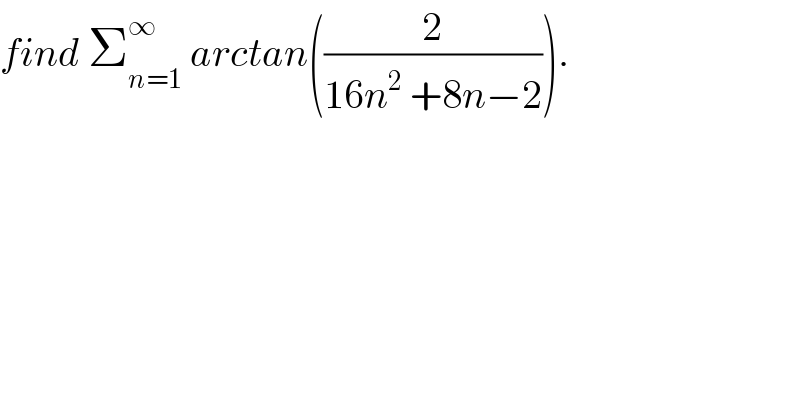
$${find}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:{arctan}\left(\frac{\mathrm{2}}{\mathrm{16}{n}^{\mathrm{2}} \:+\mathrm{8}{n}−\mathrm{2}}\right). \\ $$
Commented by rahul 19 last updated on 08/Mar/18
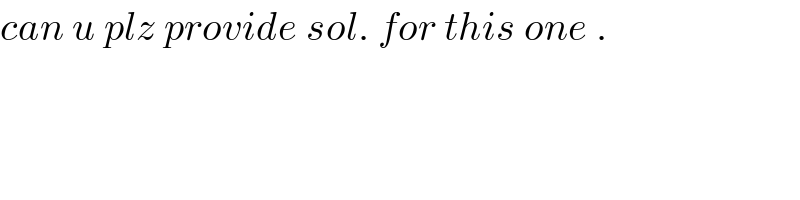
$${can}\:{u}\:{plz}\:{provide}\:{sol}.\:{for}\:{this}\:{one}\:. \\ $$
Commented by prof Abdo imad last updated on 08/Mar/18
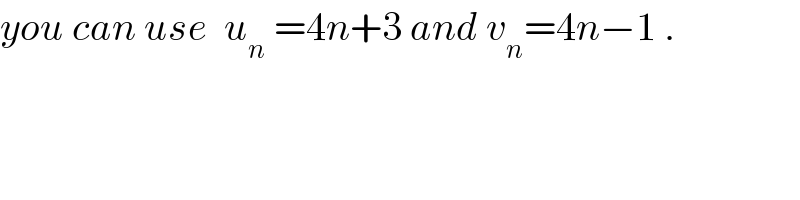
$${you}\:{can}\:{use}\:\:{u}_{{n}} \:=\mathrm{4}{n}+\mathrm{3}\:{and}\:{v}_{{n}} =\mathrm{4}{n}−\mathrm{1}\:. \\ $$
Commented by rahul 19 last updated on 08/Mar/18
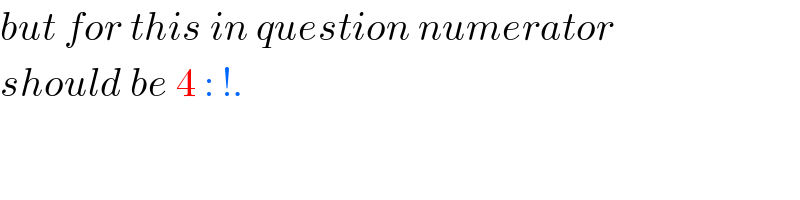
$${but}\:{for}\:{this}\:{in}\:{question}\:{numerator} \\ $$$${should}\:{be}\:\mathrm{4}\::\:!. \\ $$
Commented by abdo imad last updated on 08/Mar/18
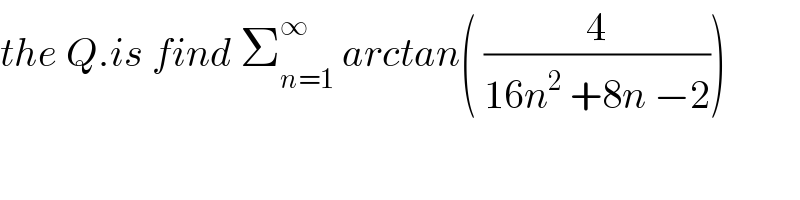
$${the}\:{Q}.{is}\:{find}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:{arctan}\left(\:\frac{\mathrm{4}}{\mathrm{16}{n}^{\mathrm{2}} \:+\mathrm{8}{n}\:−\mathrm{2}}\right) \\ $$
Commented by rahul 19 last updated on 09/Mar/18
$${yes}\:{sir}!\:{now}\:{its}\:{clear}\:{and}\:{cut}. \\ $$
Commented by abdo imad last updated on 09/Mar/18
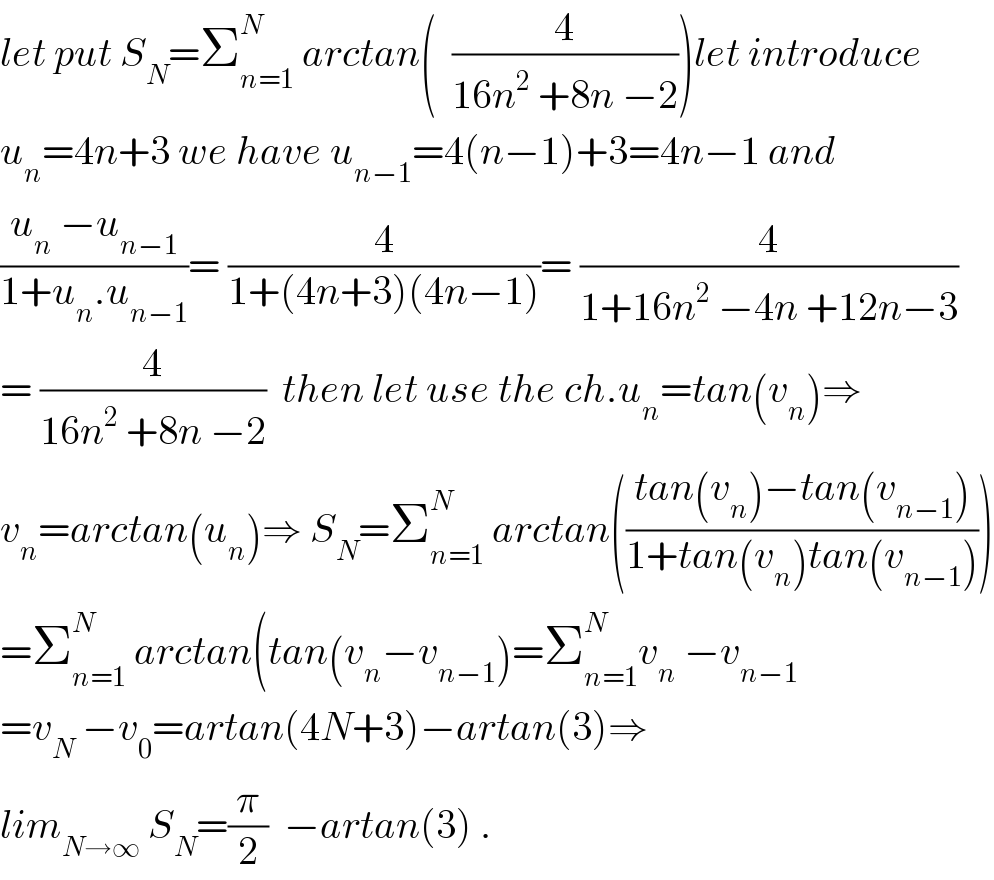
$${let}\:{put}\:{S}_{{N}} =\sum_{{n}=\mathrm{1}} ^{{N}} \:{arctan}\left(\:\:\frac{\mathrm{4}}{\mathrm{16}{n}^{\mathrm{2}} \:+\mathrm{8}{n}\:−\mathrm{2}}\right){let}\:{introduce} \\ $$$${u}_{{n}} =\mathrm{4}{n}+\mathrm{3}\:{we}\:{have}\:{u}_{{n}−\mathrm{1}} =\mathrm{4}\left({n}−\mathrm{1}\right)+\mathrm{3}=\mathrm{4}{n}−\mathrm{1}\:{and} \\ $$$$\frac{{u}_{{n}} \:−{u}_{{n}−\mathrm{1}} }{\mathrm{1}+{u}_{{n}} .{u}_{{n}−\mathrm{1}} }=\:\frac{\mathrm{4}}{\mathrm{1}+\left(\mathrm{4}{n}+\mathrm{3}\right)\left(\mathrm{4}{n}−\mathrm{1}\right)}=\:\frac{\mathrm{4}}{\mathrm{1}+\mathrm{16}{n}^{\mathrm{2}} \:−\mathrm{4}{n}\:+\mathrm{12}{n}−\mathrm{3}} \\ $$$$=\:\frac{\mathrm{4}}{\mathrm{16}{n}^{\mathrm{2}} \:+\mathrm{8}{n}\:−\mathrm{2}}\:\:{then}\:{let}\:{use}\:{the}\:{ch}.{u}_{{n}} ={tan}\left({v}_{{n}} \right)\Rightarrow \\ $$$${v}_{{n}} ={arctan}\left({u}_{{n}} \right)\Rightarrow\:{S}_{{N}} =\sum_{{n}=\mathrm{1}} ^{{N}} \:{arctan}\left(\frac{{tan}\left({v}_{{n}} \right)−{tan}\left({v}_{{n}−\mathrm{1}} \right)}{\mathrm{1}+{tan}\left({v}_{{n}} \right){tan}\left({v}_{{n}−\mathrm{1}} \right)}\right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{{N}} \:{arctan}\left({tan}\left({v}_{{n}} −{v}_{{n}−\mathrm{1}} \right)=\sum_{{n}=\mathrm{1}} ^{{N}} {v}_{{n}} \:−{v}_{{n}−\mathrm{1}} \right. \\ $$$$={v}_{{N}} \:−{v}_{\mathrm{0}} ={artan}\left(\mathrm{4}{N}+\mathrm{3}\right)−{artan}\left(\mathrm{3}\right)\Rightarrow \\ $$$${lim}_{{N}\rightarrow\infty} \:{S}_{{N}} =\frac{\pi}{\mathrm{2}}\:\:−{artan}\left(\mathrm{3}\right)\:. \\ $$
