Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 3143 by Rasheed Soomro last updated on 06/Dec/15

Suggest minimum number of weights by which we can weigh upto 40 kgs(in whole numbers) in a traditional balance. If possible mention the process also.

$$\mathcal{S}{uggest}\:{minimum}\:{number}\:{of}\:{weights}\:{by}\:{which}\:{we}\:\:{can}\: \\ $$$${weigh}\:\:{upto}\:\mathrm{40}\:{kgs}\left({in}\:{whole}\:{numbers}\right)\:{in}\:{a}\:{traditional}\:{balance}. \\ $$$${If}\:{possible}\:{mention}\:{the}\:{process}\:{also}. \\ $$

Commented by Rasheed Soomro last updated on 06/Dec/15

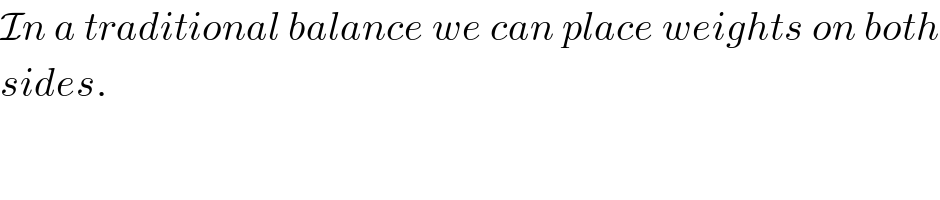
In a traditional balance we can place weights on both sides.

$$\mathcal{I}{n}\:{a}\:{traditional}\:{balance}\:{we}\:{can}\:{place}\:{weights}\:{on}\:{both} \\ $$$${sides}. \\ $$

Answered by prakash jain last updated on 06/Dec/15

You start with 1kg For 2 kg select 1+2=3kg − you get 1 to 4 for 5 kg select 4+5=9kg you get 1to 13kgs for 14kg select 13+14=27kg you get 1 to 40. so you need following weight 1,3,9,27 to weight all upto 40kg (in whole numbers).

$$\mathrm{You}\:\mathrm{start}\:\mathrm{with}\:\mathrm{1kg} \\ $$$$\mathrm{For}\:\mathrm{2}\:\mathrm{kg}\:\mathrm{select}\:\mathrm{1}+\mathrm{2}=\mathrm{3kg}\:−\:\mathrm{you}\:\mathrm{get}\:\mathrm{1}\:\mathrm{to}\:\mathrm{4} \\ $$$$\mathrm{for}\:\mathrm{5}\:\mathrm{kg}\:\mathrm{select}\:\mathrm{4}+\mathrm{5}=\mathrm{9kg}\:\mathrm{you}\:\mathrm{get}\:\mathrm{1to}\:\mathrm{13kgs} \\ $$$$\mathrm{for}\:\mathrm{14kg}\:\mathrm{select}\:\mathrm{13}+\mathrm{14}=\mathrm{27kg}\:\mathrm{you}\:\mathrm{get}\:\mathrm{1}\:\mathrm{to}\:\mathrm{40}. \\ $$$$\mathrm{so}\:\mathrm{you}\:\mathrm{need}\:\mathrm{following}\:\mathrm{weight} \\ $$$$\mathrm{1},\mathrm{3},\mathrm{9},\mathrm{27}\:\mathrm{to}\:\mathrm{weight}\:\mathrm{all}\:\mathrm{upto}\:\mathrm{40kg}\:\left(\mathrm{in}\:\mathrm{whole}\:\mathrm{numbers}\right). \\ $$

Commented by RasheedAhmad last updated on 06/Dec/15

N^V ice Sir!

$$\overset{\mathcal{V}} {\mathcal{N}}{ice}\:\mathcal{S}{ir}! \\ $$

Commented by RasheedAhmad last updated on 06/Dec/15

^(Rasheed Soomro) All are powers of 3. Next power is 81 Five weights(1,3,9,27,81) can weigh upto 1+3+9+27+81=121 kg. n weights 3^0 ,3^1 ,3^2 ,...3^(n−1) can weigh upto 3^0 +3^1 +3^2 +...+3^(n−1) =((3^n −1)/2)

$$\:^{{Rasheed}\:{Soomro}} \\ $$$$\mathcal{A}{ll}\:{are}\:{powers}\:{of}\:\mathrm{3}. \\ $$$$\mathcal{N}{ext}\:{power}\:{is}\:\mathrm{81} \\ $$$$\mathcal{F}{ive}\:{weights}\left(\mathrm{1},\mathrm{3},\mathrm{9},\mathrm{27},\mathrm{81}\right)\:{can} \\ $$$${weigh}\:{upto}\:\mathrm{1}+\mathrm{3}+\mathrm{9}+\mathrm{27}+\mathrm{81}=\mathrm{121}\:\mathrm{kg}. \\ $$$${n}\:{weights}\:\mathrm{3}^{\mathrm{0}} ,\mathrm{3}^{\mathrm{1}} ,\mathrm{3}^{\mathrm{2}} ,...\mathrm{3}^{{n}−\mathrm{1}} \:{can}\:{weigh} \\ $$$${upto}\:\mathrm{3}^{\mathrm{0}} +\mathrm{3}^{\mathrm{1}} +\mathrm{3}^{\mathrm{2}} +...+\mathrm{3}^{{n}−\mathrm{1}} \\ $$$$=\frac{\mathrm{3}^{{n}} −\mathrm{1}}{\mathrm{2}}\: \\ $$

Commented by prakash jain last updated on 06/Dec/15

Yes.

$$\mathrm{Yes}. \\ $$

Commented by Yozzi last updated on 06/Dec/15

Why is your answer correct? Why start with 1 kg,then 2kg, ...? I don′t understand your steps. (not doubting it′s wrong; I want to understand the idea behind the question.)

$${Why}\:{is}\:{your}\:{answer}\:{correct}?\:{Why} \\ $$$${start}\:{with}\:\mathrm{1}\:{kg},{then}\:\mathrm{2}{kg},\:...? \\ $$$${I}\:{don}'{t}\:{understand}\:{your}\:{steps}. \\ $$$$\left({not}\:{doubting}\:{it}'{s}\:{wrong};\:{I}\:{want}\:{to}\right. \\ $$$${understand}\:{the}\:{idea}\:{behind}\:{the} \\ $$$$\left.{question}.\right) \\ $$

Commented by prakash jain last updated on 06/Dec/15

With 1 kg you can weigh up to 1kg. To weigh 2 kg the maximum weight that we can use is 3kg. This gives the maximum range to 4 kg. 1, 3−1,3, 3+1. Similarly we use the largest possible weight every time to get the max range so that minimum number of weights are used. Since we are able to weigh 1 to 4 (with 1and3) adding 9kg will allow addition range (9−4) to (9+4). and so on. 1=1 2=3−1 3=3 4=3+1 5=9−4=9−(3+1) 6=9−3 7=9−2=9−(3−1)=9+1−3 8=9−1 9=9 10=9+1 11=9+3−1 12=9+3 13=9+3+1 When you add 27 you can get 27−(1 to 13) to 27+(1 to 13). Since 1 to 13 can be contructed without using 27kg weight. Since we can put weights on both sides of balancr subtraction is allowed.

$$\mathrm{With}\:\mathrm{1}\:\mathrm{kg}\:\mathrm{you}\:\mathrm{can}\:\mathrm{weigh}\:\mathrm{up}\:\mathrm{to}\:\mathrm{1kg}. \\ $$$$\mathrm{To}\:\mathrm{weigh}\:\mathrm{2}\:\mathrm{kg}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{weight} \\ $$$$\mathrm{that}\:\mathrm{we}\:\mathrm{can}\:\mathrm{use}\:\mathrm{is}\:\mathrm{3kg}.\:\mathrm{This}\:\mathrm{gives}\:\mathrm{the}\:\mathrm{maximum} \\ $$$$\mathrm{range}\:\mathrm{to}\:\mathrm{4}\:\mathrm{kg}.\:\mathrm{1},\:\mathrm{3}−\mathrm{1},\mathrm{3},\:\mathrm{3}+\mathrm{1}. \\ $$$$\mathrm{Similarly}\:\mathrm{we}\:\mathrm{use}\:\mathrm{the}\:\mathrm{largest}\:\mathrm{possible} \\ $$$$\mathrm{weight}\:\mathrm{every}\:\mathrm{time}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{max}\:\mathrm{range}\:\mathrm{so} \\ $$$$\mathrm{that}\:\mathrm{minimum}\:\mathrm{number}\:\mathrm{of}\:\mathrm{weights}\:\mathrm{are}\:\mathrm{used}. \\ $$$$\mathrm{Since}\:\mathrm{we}\:\mathrm{are}\:\mathrm{able}\:\mathrm{to}\:\mathrm{weigh}\:\mathrm{1}\:\mathrm{to}\:\mathrm{4}\:\left(\mathrm{with}\:\mathrm{1and3}\right) \\ $$$$\mathrm{adding}\:\mathrm{9kg}\:\mathrm{will}\:\mathrm{allow}\:\mathrm{addition}\:\mathrm{range} \\ $$$$\left(\mathrm{9}−\mathrm{4}\right)\:\mathrm{to}\:\left(\mathrm{9}+\mathrm{4}\right). \\ $$$$\mathrm{and}\:\mathrm{so}\:\mathrm{on}. \\ $$$$\mathrm{1}=\mathrm{1} \\ $$$$\mathrm{2}=\mathrm{3}−\mathrm{1} \\ $$$$\mathrm{3}=\mathrm{3} \\ $$$$\mathrm{4}=\mathrm{3}+\mathrm{1} \\ $$$$\mathrm{5}=\mathrm{9}−\mathrm{4}=\mathrm{9}−\left(\mathrm{3}+\mathrm{1}\right) \\ $$$$\mathrm{6}=\mathrm{9}−\mathrm{3} \\ $$$$\mathrm{7}=\mathrm{9}−\mathrm{2}=\mathrm{9}−\left(\mathrm{3}−\mathrm{1}\right)=\mathrm{9}+\mathrm{1}−\mathrm{3} \\ $$$$\mathrm{8}=\mathrm{9}−\mathrm{1} \\ $$$$\mathrm{9}=\mathrm{9} \\ $$$$\mathrm{10}=\mathrm{9}+\mathrm{1} \\ $$$$\mathrm{11}=\mathrm{9}+\mathrm{3}−\mathrm{1} \\ $$$$\mathrm{12}=\mathrm{9}+\mathrm{3} \\ $$$$\mathrm{13}=\mathrm{9}+\mathrm{3}+\mathrm{1} \\ $$$$\mathrm{When}\:\mathrm{you}\:\mathrm{add}\:\mathrm{27}\:\mathrm{you}\:\mathrm{can}\:\mathrm{get}\:\mathrm{27}−\left(\mathrm{1}\:\mathrm{to}\:\mathrm{13}\right)\:\mathrm{to} \\ $$$$\mathrm{27}+\left(\mathrm{1}\:\mathrm{to}\:\mathrm{13}\right).\:\mathrm{Since}\:\mathrm{1}\:\mathrm{to}\:\mathrm{13}\:\mathrm{can}\:\mathrm{be}\:\mathrm{contructed} \\ $$$$\mathrm{without}\:\mathrm{using}\:\mathrm{27kg}\:\mathrm{weight}. \\ $$$$\mathrm{Since}\:\mathrm{we}\:\mathrm{can}\:\mathrm{put}\:\mathrm{weights}\:\mathrm{on}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{of} \\ $$$$\mathrm{balancr}\:\mathrm{subtraction}\:\mathrm{is}\:\mathrm{allowed}. \\ $$

Commented by prakash jain last updated on 07/Dec/15

Suppose you have n weight. The possible weights that you can create (including −ve and duplicates) are. choose 1 and put a +/− sign before it=2^n C_1 choose 2 and put a +/− sign before each=2^2 ^n C_2 and so on So total number of sum that you can obtain with n +ve numbers are=Σ_(i=1) ^n 2^i ^n C_i (1+2)^n =^n C_0 +2∙^n C_1 +2^2 ^n C_2 +...+2^n ^n C_n 3^n =1+Σ_(i=1) ^n 2^i ^n C_i Σ_(i=1) ^n 2^i ^n C_i =3^n −1 with 3 +ve number you can create=3^3 −1=26 half of them will be −ve so 13 +ve number. with 4 +ve number you can create 3^4 −1=80 or 40 +ve numbers. This proves that you need a minimum of 4 weights to create 40 +ve results. Solving the question is about finding 4 numbers so the sums are 1 to 40.

$$\mathrm{Suppose}\:\mathrm{you}\:\mathrm{have}\:{n}\:\mathrm{weight}.\:\mathrm{The}\:\mathrm{possible} \\ $$$$\mathrm{weights}\:\mathrm{that}\:\mathrm{you}\:\mathrm{can}\:\mathrm{create}\:\left(\mathrm{including}\right. \\ $$$$\left.−\mathrm{ve}\:\mathrm{and}\:\mathrm{duplicates}\right)\:\mathrm{are}. \\ $$$$\mathrm{choose}\:\mathrm{1}\:\mathrm{and}\:\mathrm{put}\:\mathrm{a}\:+/−\:\mathrm{sign}\:\mathrm{before}\:\mathrm{it}=\mathrm{2}\:^{{n}} {C}_{\mathrm{1}} \\ $$$$\mathrm{choose}\:\mathrm{2}\:\mathrm{and}\:\mathrm{put}\:\mathrm{a}\:+/−\:\mathrm{sign}\:\mathrm{before}\:\mathrm{each}=\mathrm{2}^{\mathrm{2}} \:^{{n}} {C}_{\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{so}\:\mathrm{on}\: \\ $$$$\mathrm{So}\:\mathrm{total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{sum}\:\mathrm{that}\:\mathrm{you}\:\mathrm{can} \\ $$$$\mathrm{obtain}\:\mathrm{with}\:{n}\:+{ve}\:\mathrm{numbers}\:\mathrm{are}=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{2}^{{i}} \:^{{n}} {C}_{{i}} \\ $$$$\left(\mathrm{1}+\mathrm{2}\right)^{{n}} =\:^{{n}} {C}_{\mathrm{0}} +\mathrm{2}\centerdot\:^{{n}} {C}_{\mathrm{1}} +\mathrm{2}^{\mathrm{2}} \:^{{n}} {C}_{\mathrm{2}} +...+\mathrm{2}^{{n}} \:^{{n}} {C}_{{n}} \\ $$$$\mathrm{3}^{{n}} =\mathrm{1}+\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\:\mathrm{2}^{{i}} \:^{{n}} {C}_{{i}} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\:\mathrm{2}^{{i}} \:^{{n}} {C}_{{i}} =\mathrm{3}^{{n}} −\mathrm{1} \\ $$$${with}\:\mathrm{3}\:+\mathrm{ve}\:{number}\:{you}\:{can}\:{create}=\mathrm{3}^{\mathrm{3}} −\mathrm{1}=\mathrm{26}\: \\ $$$$\mathrm{half}\:\mathrm{of}\:\mathrm{them}\:\mathrm{will}\:\mathrm{be}\:−\mathrm{ve}\:\mathrm{so}\:\mathrm{13}\:+\mathrm{ve}\:\mathrm{number}. \\ $$$$\mathrm{with}\:\mathrm{4}\:+\mathrm{ve}\:\mathrm{number}\:\mathrm{you}\:\mathrm{can}\:\mathrm{create}\:\mathrm{3}^{\mathrm{4}} −\mathrm{1}=\mathrm{80} \\ $$$$\mathrm{or}\:\mathrm{40}\:+\mathrm{ve}\:\mathrm{numbers}. \\ $$$$\mathrm{This}\:\mathrm{proves}\:\mathrm{that}\:\mathrm{you}\:\mathrm{need}\:\mathrm{a}\:\mathrm{minimum}\:\mathrm{of} \\ $$$$\mathrm{4}\:\mathrm{weights}\:\mathrm{to}\:\mathrm{create}\:\mathrm{40}\:+\mathrm{ve}\:\mathrm{results}. \\ $$$$\mathrm{Solving}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{about}\:\mathrm{finding}\:\mathrm{4}\:\mathrm{numbers} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{sums}\:\mathrm{are}\:\mathrm{1}\:\mathrm{to}\:\mathrm{40}. \\ $$

Commented by Yozzi last updated on 06/Dec/15

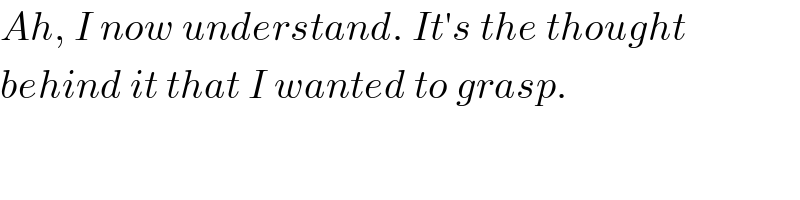
Ah, I now understand. It′s the thought behind it that I wanted to grasp.

$${Ah},\:{I}\:{now}\:{understand}.\:{It}'{s}\:{the}\:{thought} \\ $$$${behind}\:{it}\:{that}\:{I}\:{wanted}\:{to}\:{grasp}.\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com