
Previous in Relation and Functions Next in Relation and Functions
Question Number 31500 by abdo imad last updated on 09/Mar/18
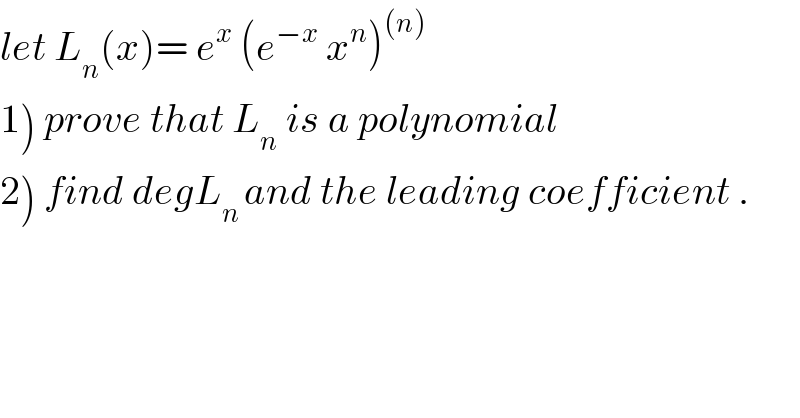
$${let}\:{L}_{{n}} \left({x}\right)=\:{e}^{{x}} \:\left({e}^{−{x}} \:{x}^{{n}} \right)^{\left({n}\right)} \: \\ $$$$\left.\mathrm{1}\right)\:{prove}\:{that}\:{L}_{{n}} \:{is}\:{a}\:{polynomial} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{degL}_{{n}\:} {and}\:{the}\:{leading}\:{coefficient}\:. \\ $$
Commented by abdo imad last updated on 13/Mar/18

$${we}\:{have}\:{by}\:{Leniz}\:{formulae}\: \\ $$$$\left({e}^{−{x}} \:{x}^{{n}} \right)^{\left({n}\right)} \:=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\:\left({x}^{{n}} \right)^{\left({k}\right)} \:\left({e}^{−{x}} \right)^{\left({n}−{k}\right)} \:{but} \\ $$$$\:\left({x}^{{n}} \right)^{\left({k}\right)} ={n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)...\left({n}−{k}+\mathrm{1}\right)\:{x}^{{n}−{k}} \\ $$$$=\frac{{n}!}{\left({n}−{k}\right)!}\:{x}^{{n}−{k}} \:\:\:{and}\:\:\left({e}^{−{x}} \right)^{\left({n}−{k}\right)} =\left(−\mathrm{1}\right)^{{n}−{k}} \:{e}^{−{x}} \:\Rightarrow \\ $$$$\left({e}^{−{x}} \:{x}^{{n}} \right)^{\left({n}\right)} \:\:=\:{e}^{−{x}} \sum_{{k}=\mathrm{0}} ^{{n}} \:\left(−\mathrm{1}\right)^{{n}−{k}} \:{C}_{{n}} ^{{k}} \:\:\frac{{n}!}{\left({n}−{k}\right)!}\:{x}^{{n}−{k}} \:\:\Rightarrow \\ $$$${L}_{{n}} \left({x}\right)=\left(−\mathrm{1}\right)^{{n}} \:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\left(−\mathrm{1}\right)^{{k}} \:{C}_{{n}} ^{{k}} \:\:\:\frac{{n}!}{\left({n}−{k}\right)!}\:{x}^{{n}−{k}} \:\:{ch}.{of}\:{indice} \\ $$$${n}−{k}={p}\:{give}\:{L}_{{n}} \left({x}\right)=\left(−\mathrm{1}\right)^{{n}} \:\sum_{{p}=\mathrm{0}} ^{{n}} \left(−\mathrm{1}\right)^{{n}−{p}} \:\:{C}_{{n}} ^{{n}−{p}} \:\frac{{n}!}{{p}!}\:{x}^{{p}} \\ $$$${L}_{{n}} \left({x}\right)=\:\sum_{{p}=\mathrm{0}} ^{{n}} \:\left(−\mathrm{1}\right)^{{p}} \:\:{C}_{{n}} ^{{p}} \:\:\frac{{n}!}{{p}!}\:{x}^{{p}} \:\:{and}\:{is}\:{a}\:{polynomial} \\ $$$$\left.\mathrm{2}\right)\:{its}\:{clear}\:{that}\:{deg}\:{L}_{{n}} ={n}\:{and}\:{the}\:{leading}\:{coefficient}\:{is} \\ $$$$\left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}} \:. \\ $$
Commented by abdo imad last updated on 13/Mar/18
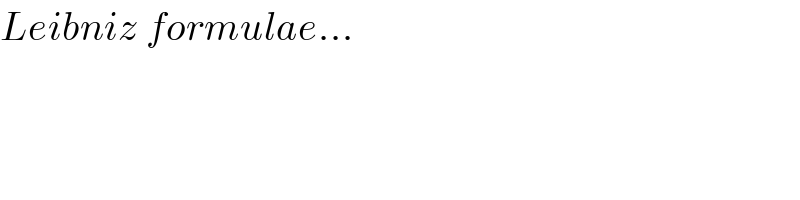
$${Leibniz}\:{formulae}... \\ $$
Commented by abdo imad last updated on 13/Mar/18
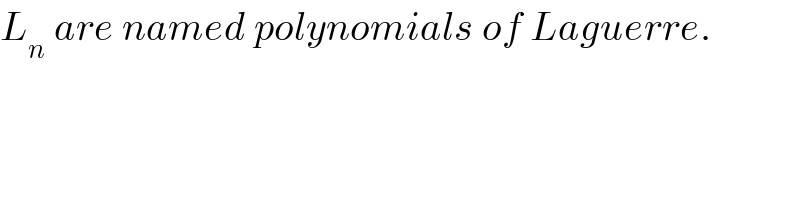
$${L}_{{n}} \:{are}\:{named}\:{polynomials}\:{of}\:{Laguerre}. \\ $$
