
Question and Answers Forum
Question Number 31515 by abdo imad last updated on 09/Mar/18
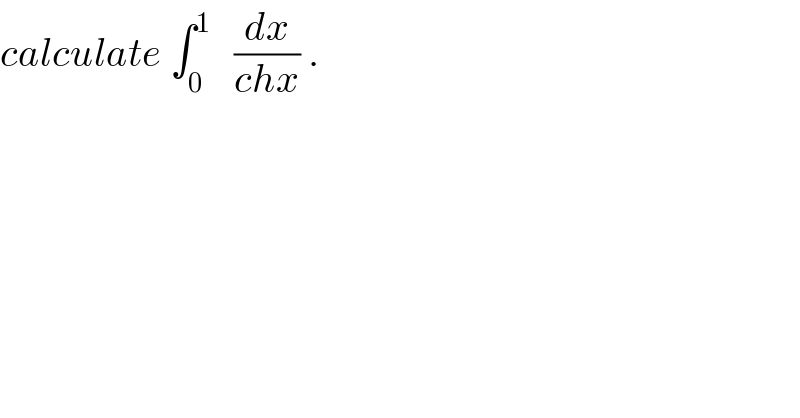
Commented by abdo imad last updated on 10/Mar/18
![I= ∫_0 ^1 (dx/((e^x +e^(−x) )/2))=2 ∫_0 ^1 (dx/(e^x +e^(−x) )) the ch .e^x =t give I=2 ∫_1 ^e (1/(t +(1/t))) (dt/t)= 2∫_1 ^e (dt/(t^2 +1))=2[arctant]_1 ^e =2 arctane −(π/2) .](Q31581.png)
Answered by sma3l2996 last updated on 10/Mar/18
![I=∫_0 ^1 (dx/(cosh(x))) t=tanh(x/2)⇒2dt=(1−(tanh(x/2))^2 )dx cosh(x)=2cosh^2 (x/2)−1=(2/(1−tanh^2 (x/2)))−1 cosh(x)=((1+tanh^2 (x/2))/(1−tanh^2 (x/2)))=((1+t^2 )/(1−t^2 )) I=∫_0 ^(tanh(1/2)) ((1−t^2 )/(1+t^2 ))×(((2dt)/(1−t^2 )))=2∫_0 ^(tanh(1/2)) (dt/(1+t^2 )) I=2[tan^(−1) (t)]_0 ^(tanh(1/2)) I=2tan^(−1) (tanh(1/2))](Q31554.png)
| ||
Question and Answers Forum | ||
Question Number 31515 by abdo imad last updated on 09/Mar/18 | ||
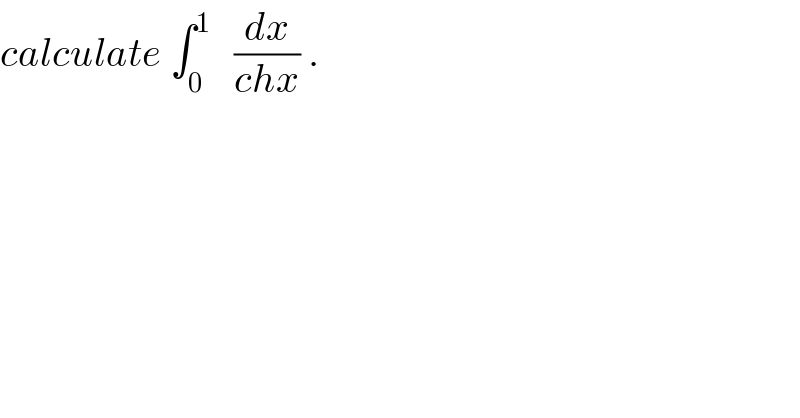 | ||
Commented by abdo imad last updated on 10/Mar/18 | ||
![I= ∫_0 ^1 (dx/((e^x +e^(−x) )/2))=2 ∫_0 ^1 (dx/(e^x +e^(−x) )) the ch .e^x =t give I=2 ∫_1 ^e (1/(t +(1/t))) (dt/t)= 2∫_1 ^e (dt/(t^2 +1))=2[arctant]_1 ^e =2 arctane −(π/2) .](Q31581.png) | ||
Answered by sma3l2996 last updated on 10/Mar/18 | ||
![I=∫_0 ^1 (dx/(cosh(x))) t=tanh(x/2)⇒2dt=(1−(tanh(x/2))^2 )dx cosh(x)=2cosh^2 (x/2)−1=(2/(1−tanh^2 (x/2)))−1 cosh(x)=((1+tanh^2 (x/2))/(1−tanh^2 (x/2)))=((1+t^2 )/(1−t^2 )) I=∫_0 ^(tanh(1/2)) ((1−t^2 )/(1+t^2 ))×(((2dt)/(1−t^2 )))=2∫_0 ^(tanh(1/2)) (dt/(1+t^2 )) I=2[tan^(−1) (t)]_0 ^(tanh(1/2)) I=2tan^(−1) (tanh(1/2))](Q31554.png) | ||
| ||