
Question and Answers Forum
Question Number 31639 by Tinkutara last updated on 11/Mar/18

Answered by MJS last updated on 11/Mar/18
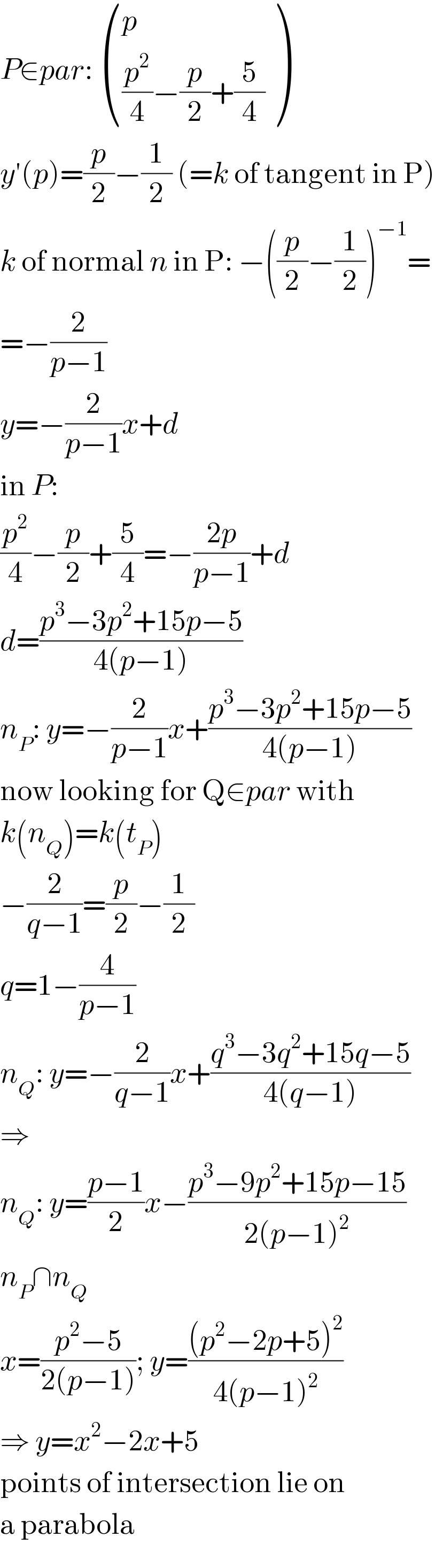
Commented by Tinkutara last updated on 11/Mar/18
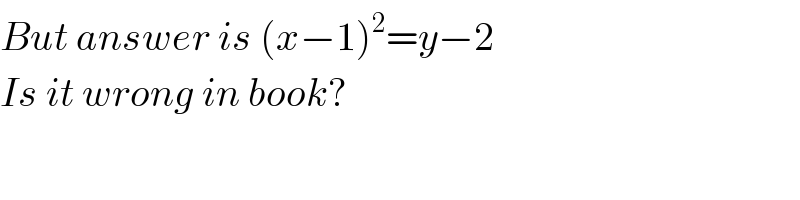
Commented by MJS last updated on 11/Mar/18
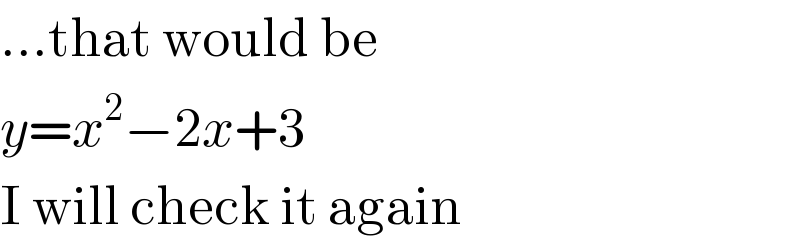
Commented by MJS last updated on 11/Mar/18

Commented by Tinkutara last updated on 12/Mar/18

Commented by MJS last updated on 12/Mar/18
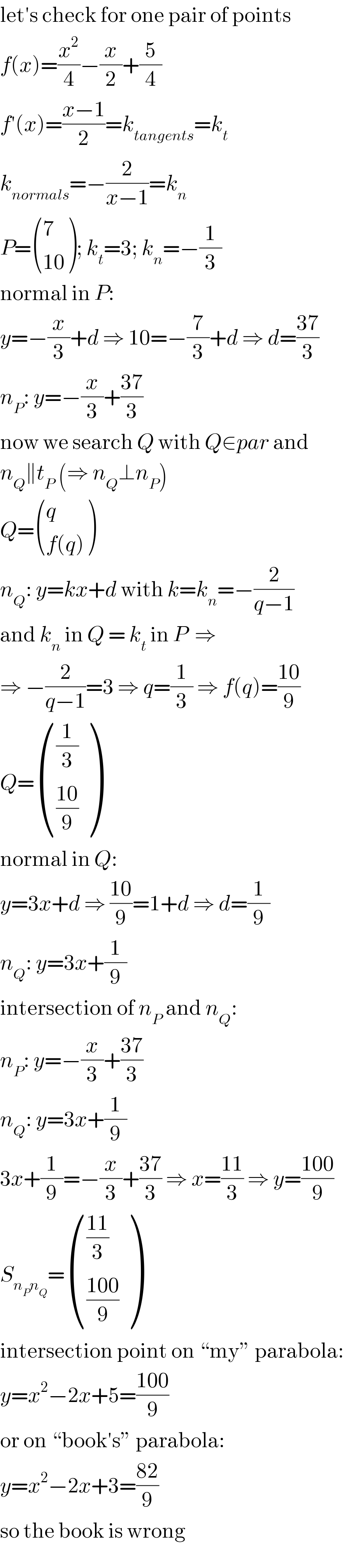
Commented by Tinkutara last updated on 12/Mar/18
Thank you very much Sir! I got the answer. ��������
