
Question and Answers Forum
Question Number 31804 by rahul 19 last updated on 15/Mar/18
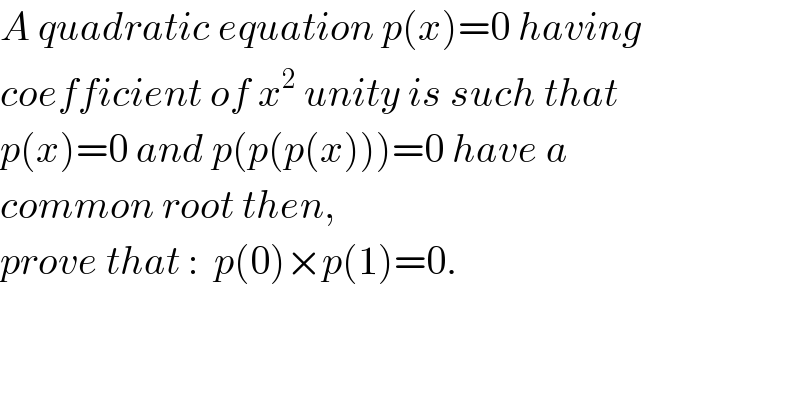
Answered by MJS last updated on 15/Mar/18
![p(x)=x^2 +bx+c p(0)×p(1)=0 ⇒ p(0)=0∨p(1)=0 case 1 p(0)=0 ⇒ c=0 p(x)=(x+b)x p(p(x))=q(x) p(p(p(x)))=p(q(x))=r(x) q(x)=(p(x)+b)p(x) ⇒ ⇒ q(0)=0 r(x)=(q(x)+b)q(x) ⇒ ⇒ r(0)=0 ⇒ ⇒ 0= common root of p(x) and r(x) case 2 p(1)=0 p(x)=(x−1)(x−c) [with b=−c−1; p(x)=x^2 −(c+1)x+c] q(x)=(p(x)−1)(p(x)−c)= =p^2 (x)−(c+1)p(x)+c r(x)=[p^2 (x)−(c+1)p(x)+c−1]× ×[p^2 (x)−(c+1)p(x)]= =[...]×[p(x)−(c+1)]×p(x) ⇒ ⇒ r(1)=0 ⇒ ⇒ 1= common root of p(x) and r(x)](Q31827.png)
| ||
Question and Answers Forum | ||
Question Number 31804 by rahul 19 last updated on 15/Mar/18 | ||
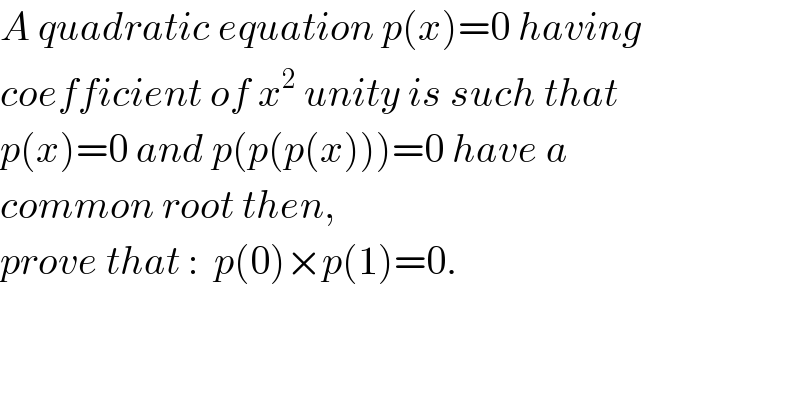 | ||
Answered by MJS last updated on 15/Mar/18 | ||
![p(x)=x^2 +bx+c p(0)×p(1)=0 ⇒ p(0)=0∨p(1)=0 case 1 p(0)=0 ⇒ c=0 p(x)=(x+b)x p(p(x))=q(x) p(p(p(x)))=p(q(x))=r(x) q(x)=(p(x)+b)p(x) ⇒ ⇒ q(0)=0 r(x)=(q(x)+b)q(x) ⇒ ⇒ r(0)=0 ⇒ ⇒ 0= common root of p(x) and r(x) case 2 p(1)=0 p(x)=(x−1)(x−c) [with b=−c−1; p(x)=x^2 −(c+1)x+c] q(x)=(p(x)−1)(p(x)−c)= =p^2 (x)−(c+1)p(x)+c r(x)=[p^2 (x)−(c+1)p(x)+c−1]× ×[p^2 (x)−(c+1)p(x)]= =[...]×[p(x)−(c+1)]×p(x) ⇒ ⇒ r(1)=0 ⇒ ⇒ 1= common root of p(x) and r(x)](Q31827.png) | ||
| ||