Question Number 31915 by rahul 19 last updated on 16/Mar/18
$$\boldsymbol{{If}}\::\: \\ $$$$\left({x}^{\mathrm{2}} +{x}+\mathrm{2}\right)^{\mathrm{2}} −\left({a}−\mathrm{3}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{2}\right) \\ $$$$+\:\left({a}−\mathrm{4}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0}\:{has}\:{at}\:{least}\: \\ $$$${one}\:{root}\:,\:{then}\:{find}\:{complete}\:{set}\:{of}\: \\ $$$${values}\:{of}\:{a}. \\ $$
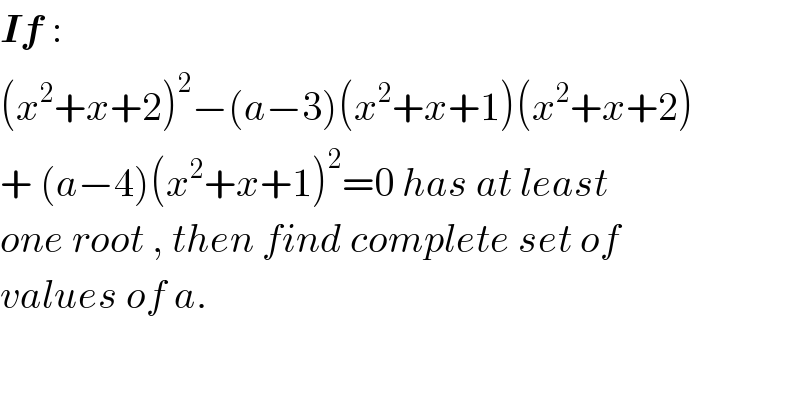
Commented by rahul 19 last updated on 16/Mar/18
![my try : let x^2 +x+1= t. ⇒ (t+1)^2 −(a−3)t(t+1)+(a−4)t^2 =0 since it has atleast one root, ⇒ Discriminant =0 ⇒(a−3)^2 t^2 −4t^2 (a−4)≥0 ⇒a^2 t^2 +25t^2 −10at^2 ≥0 ⇒t^2 (a−5)^2 ≥0 ⇒a≥5 ( t≠0) hence range = [5,∞). but correct ans. is (5,((19)/3)].](Q31917.png)
$${my}\:{try}\:: \\ $$$${let}\:{x}^{\mathrm{2}} +{x}+\mathrm{1}=\:{t}. \\ $$$$\Rightarrow\:\left({t}+\mathrm{1}\right)^{\mathrm{2}} −\left({a}−\mathrm{3}\right){t}\left({t}+\mathrm{1}\right)+\left({a}−\mathrm{4}\right){t}^{\mathrm{2}} =\mathrm{0} \\ $$$${since}\:{it}\:{has}\:{atleast}\:{one}\:{root}, \\ $$$$\Rightarrow\:{Discriminant}\:=\mathrm{0} \\ $$$$\Rightarrow\left({a}−\mathrm{3}\right)^{\mathrm{2}} {t}^{\mathrm{2}} −\mathrm{4}{t}^{\mathrm{2}} \left({a}−\mathrm{4}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{2}} {t}^{\mathrm{2}} +\mathrm{25}{t}^{\mathrm{2}} −\mathrm{10}{at}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\Rightarrow{t}^{\mathrm{2}} \left({a}−\mathrm{5}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\Rightarrow{a}\geqslant\mathrm{5}\:\left(\:{t}\neq\mathrm{0}\right)\:{hence}\:{range}\:=\:\left[\mathrm{5},\infty\right). \\ $$$${but}\:{correct}\:{ans}.\:{is}\:\left(\mathrm{5},\frac{\mathrm{19}}{\mathrm{3}}\right].\: \\ $$
Commented by mrW2 last updated on 16/Mar/18
$${Discriminant}\:{may}\:{not}\:{contain}\:{the} \\ $$$${variable}\:{itself}.\:{it}\:{can}\:{only}\:{contain} \\ $$$${the}\:{constants}. \\ $$$${correct}: \\ $$$${ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$${D}={b}^{\mathrm{2}} −\mathrm{4}{ac} \\ $$$$ \\ $$$${not}\:{correct}: \\ $$$${ax}^{\mathrm{2}} +{b}\left({x}+{d}\right){x}+{c}=\mathrm{0} \\ $$$${D}={b}^{\mathrm{2}} \left({x}+{d}\right)^{\mathrm{2}} −\mathrm{4}{ac} \\ $$
Commented by rahul 19 last updated on 18/Mar/18
$$\boldsymbol{{O}}{kay}\:{sir}. \\ $$
Answered by mrW2 last updated on 16/Mar/18
$${let}\:{t}={x}^{\mathrm{2}} +{x}+\mathrm{1} \\ $$$$\left({t}+\mathrm{1}\right)^{\mathrm{2}} −\left({a}−\mathrm{3}\right){t}\left({t}+\mathrm{1}\right)+\left({a}−\mathrm{4}\right){t}^{\mathrm{2}} =\mathrm{0} \\ $$$${t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}−\left({a}−\mathrm{3}\right){t}^{\mathrm{2}} −\left({a}−\mathrm{3}\right){t}+\left({a}−\mathrm{4}\right){t}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{5}−{a}\right){t}+\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{5}−{a}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)+\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{5}−{a}\right){x}^{\mathrm{2}} +\left(\mathrm{5}−{a}\right){x}+\left(\mathrm{6}−{a}\right)=\mathrm{0} \\ $$$${a}\neq\mathrm{5} \\ $$$${D}=\left(\mathrm{5}−{a}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{5}−{a}\right)\left(\mathrm{6}−{a}\right)\geqslant\mathrm{0} \\ $$$$\left(\mathrm{5}−{a}\right)\left(\mathrm{3}{a}−\mathrm{19}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{5}<{a}\leqslant\frac{\mathrm{19}}{\mathrm{3}} \\ $$
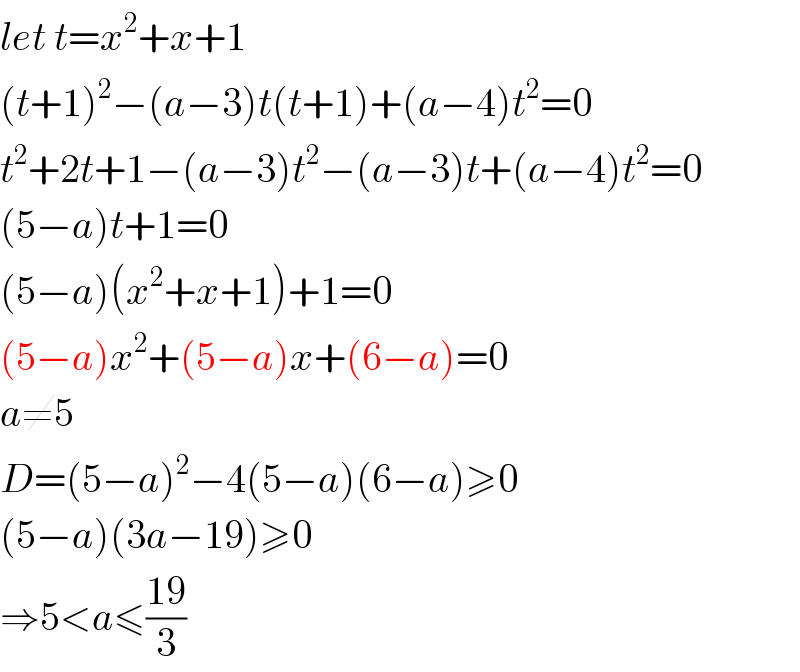
Commented by rahul 19 last updated on 18/Mar/18
$${thank}\:{u}\:{so}\:{much}\:{sir}! \\ $$