
Question and Answers Forum
Question Number 31967 by abdo imad last updated on 17/Mar/18
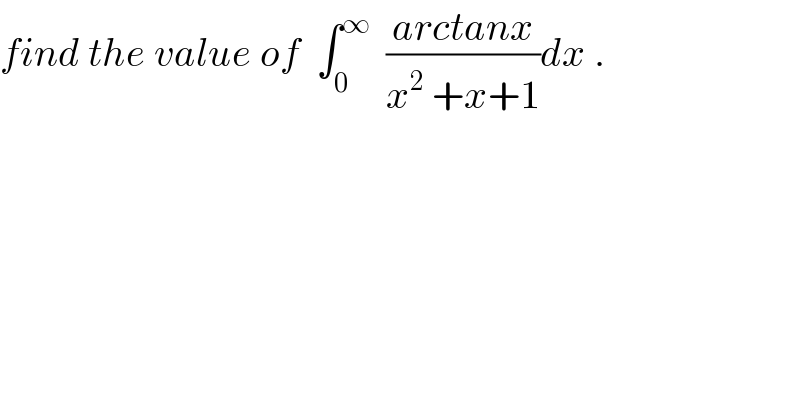
Commented by abdo imad last updated on 19/Mar/18
![let put I =∫_0 ^∞ ((arctanx)/(x^2 +x+1))dx .ch.x=(1/t) give I = ∫_0 ^∞ (((π/2) −arctant)/((1/t^2 ) +(1/t) +1)) (dt/t^2 ) = ∫_0 ^∞ (((π/2) −arctant)/(1+t +t^2 )) dt =(π/2) ∫_0 ^∞ (dt/(t^(2 ) +t +1)) −I ⇒ 2I= (π/2) ∫_0 ^∞ (dt/(t^2 +t+1)) ⇒ I =(π/4) ∫_0 ^∞ (dt/(t^2 +t +1)) .but ∫_0 ^∞ (dt/(t^2 +t +1)) = ∫_0 ^∞ (dt/((t+(1/2))^2 +(3/4)))( .ch.t+(1/2) =((√3)/2) u) = ∫_(1/(√3)) ^(+∞) (1/((3/4)(t^(2 ) +1))) ((√3)/2) du = (4/3) ((√3)/2) ∫_(1/(√3)) ^(+∞) (du/(1+u^2 )) =((2(√3))/3) [arctan(u)]_((1/(√3)) ) ^∞ =((2(√3))/3) ( (π/2) −arctan((1/(√3)))) =((2(√3))/3) arctan((√3))=((2(√3))/3) (π/3) =((2π(√3))/9) ⇒ I =(π/4) ((2π(√3))/9) = ((π^2 (√3))/(18)) .](Q32073.png)
| ||
Question and Answers Forum | ||
Question Number 31967 by abdo imad last updated on 17/Mar/18 | ||
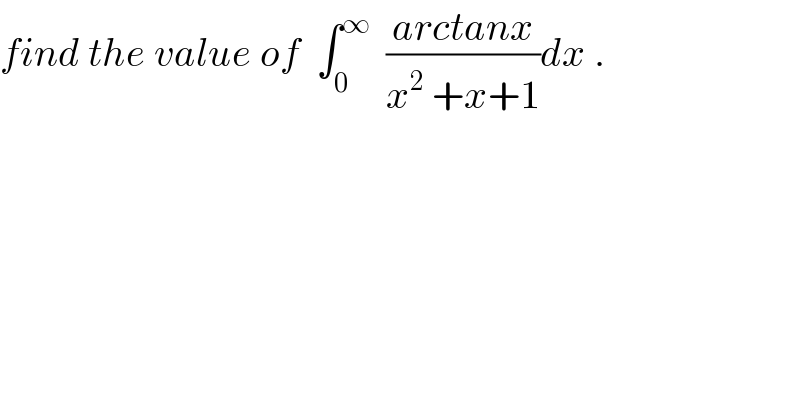 | ||
Commented by abdo imad last updated on 19/Mar/18 | ||
![let put I =∫_0 ^∞ ((arctanx)/(x^2 +x+1))dx .ch.x=(1/t) give I = ∫_0 ^∞ (((π/2) −arctant)/((1/t^2 ) +(1/t) +1)) (dt/t^2 ) = ∫_0 ^∞ (((π/2) −arctant)/(1+t +t^2 )) dt =(π/2) ∫_0 ^∞ (dt/(t^(2 ) +t +1)) −I ⇒ 2I= (π/2) ∫_0 ^∞ (dt/(t^2 +t+1)) ⇒ I =(π/4) ∫_0 ^∞ (dt/(t^2 +t +1)) .but ∫_0 ^∞ (dt/(t^2 +t +1)) = ∫_0 ^∞ (dt/((t+(1/2))^2 +(3/4)))( .ch.t+(1/2) =((√3)/2) u) = ∫_(1/(√3)) ^(+∞) (1/((3/4)(t^(2 ) +1))) ((√3)/2) du = (4/3) ((√3)/2) ∫_(1/(√3)) ^(+∞) (du/(1+u^2 )) =((2(√3))/3) [arctan(u)]_((1/(√3)) ) ^∞ =((2(√3))/3) ( (π/2) −arctan((1/(√3)))) =((2(√3))/3) arctan((√3))=((2(√3))/3) (π/3) =((2π(√3))/9) ⇒ I =(π/4) ((2π(√3))/9) = ((π^2 (√3))/(18)) .](Q32073.png) | ||