
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 95215 by mathmax by abdo last updated on 24/May/20
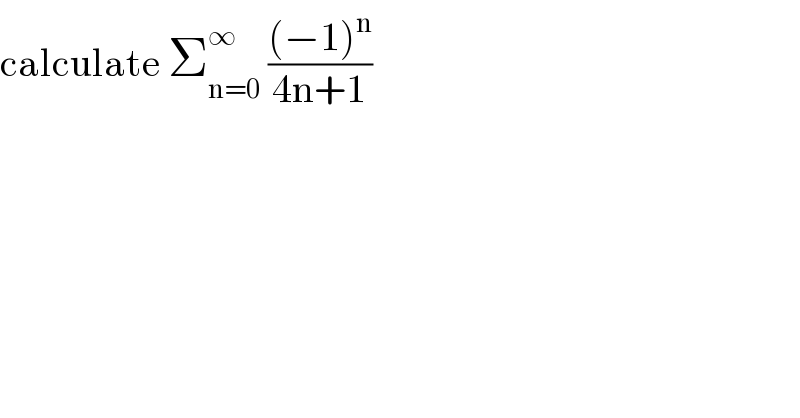
Answered by mathmax by abdo last updated on 25/May/20
![let s(x) =Σ_(n=0) ^∞ (((−1)^n )/(4n+1))x^(4n+1) with ∣x∣ ≤1 and x≠−1 s^′ (x) =Σ_(n=0) ^∞ (−1)^n x^(4n) =Σ_(n=0) ^∞ (−x^4 )^n =(1/(1+x^4 )) ⇒ s(x) =∫_0 ^x (dt/(t^4 +1)) +c s(0) =0 =c ⇒s(x) =∫_0 ^x (dt/(t^4 +1)) and Σ_(n=0) ^∞ (((−1)^n )/(4n+1)) =∫_0 ^1 (dt/(t^4 +1)) =∫_0 ^1 ((1/t^2 )/(t^2 +(1/t^2 )))dt =(1/2)∫_0 ^1 ((1+(1/t^2 )−1+(1/t^2 ))/(t^2 +(1/t^2 )))dt =(1/2)∫_0 ^1 ((1+(1/t^2 ))/(t^2 +(1/t^2 )))dt−(1/2)∫_0 ^1 ((1−(1/t^2 ))/(t^2 +(1/t^2 )))dt =(1/2) ∫_0 ^1 ((1+(1/t^2 ))/((t−(1/t))^2 +2))dt(→t−(1/t)=u)−(1/2) ∫_0 ^1 ((1−(1/t^2 ))/((t+(1/t))^2 −2))dt(→t+(1/t)=v) =(1/2) ∫_(−∞) ^0 (du/(u^2 +2)) −(1/2) ∫_(+∞) ^2 (dv/(v^2 −2)) we have ∫_(−∞) ^0 (du/(u^2 +2)) =_(u =(√2)α) ∫_(−∞) ^0 (((√2)dα)/(2(1+α^2 ))) =(1/(√2)) [arctanα]_(−∞) ^0 =(1/(√2))((π/2)) =(π/(2(√2))) and ∫_∞ ^2 (dv/(v^2 −2)) =−∫_2 ^∞ (dv/((v−(√2))(v+(√2)))) =−(1/(2(√2)))∫_2 ^(+∞) ((1/(v−(√2)))−(1/(v+(√2))))dv =−(1/(2(√2)))[ln∣((v−(√2))/(v+(√2)))∣]_2 ^(+∞) =−(1/(2(√2)))(−ln(((2−(√2))/(2(√2))))) =(1/(2(√2)))ln((1/(√2))−(1/2)) ⇒ Σ_(n=0) ^∞ (((−1)^n )/(4n+1)) =(π/(4(√2))) −(1/(4(√2)))ln((1/(√2))−(1/2))](Q95463.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 95215 by mathmax by abdo last updated on 24/May/20 | ||
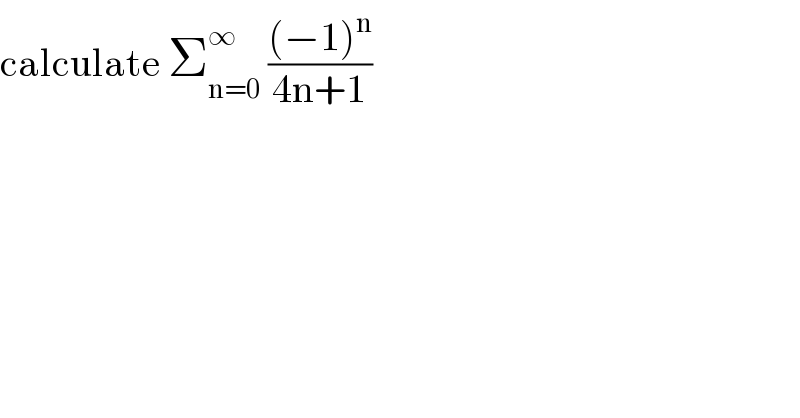 | ||
Answered by mathmax by abdo last updated on 25/May/20 | ||
![let s(x) =Σ_(n=0) ^∞ (((−1)^n )/(4n+1))x^(4n+1) with ∣x∣ ≤1 and x≠−1 s^′ (x) =Σ_(n=0) ^∞ (−1)^n x^(4n) =Σ_(n=0) ^∞ (−x^4 )^n =(1/(1+x^4 )) ⇒ s(x) =∫_0 ^x (dt/(t^4 +1)) +c s(0) =0 =c ⇒s(x) =∫_0 ^x (dt/(t^4 +1)) and Σ_(n=0) ^∞ (((−1)^n )/(4n+1)) =∫_0 ^1 (dt/(t^4 +1)) =∫_0 ^1 ((1/t^2 )/(t^2 +(1/t^2 )))dt =(1/2)∫_0 ^1 ((1+(1/t^2 )−1+(1/t^2 ))/(t^2 +(1/t^2 )))dt =(1/2)∫_0 ^1 ((1+(1/t^2 ))/(t^2 +(1/t^2 )))dt−(1/2)∫_0 ^1 ((1−(1/t^2 ))/(t^2 +(1/t^2 )))dt =(1/2) ∫_0 ^1 ((1+(1/t^2 ))/((t−(1/t))^2 +2))dt(→t−(1/t)=u)−(1/2) ∫_0 ^1 ((1−(1/t^2 ))/((t+(1/t))^2 −2))dt(→t+(1/t)=v) =(1/2) ∫_(−∞) ^0 (du/(u^2 +2)) −(1/2) ∫_(+∞) ^2 (dv/(v^2 −2)) we have ∫_(−∞) ^0 (du/(u^2 +2)) =_(u =(√2)α) ∫_(−∞) ^0 (((√2)dα)/(2(1+α^2 ))) =(1/(√2)) [arctanα]_(−∞) ^0 =(1/(√2))((π/2)) =(π/(2(√2))) and ∫_∞ ^2 (dv/(v^2 −2)) =−∫_2 ^∞ (dv/((v−(√2))(v+(√2)))) =−(1/(2(√2)))∫_2 ^(+∞) ((1/(v−(√2)))−(1/(v+(√2))))dv =−(1/(2(√2)))[ln∣((v−(√2))/(v+(√2)))∣]_2 ^(+∞) =−(1/(2(√2)))(−ln(((2−(√2))/(2(√2))))) =(1/(2(√2)))ln((1/(√2))−(1/2)) ⇒ Σ_(n=0) ^∞ (((−1)^n )/(4n+1)) =(π/(4(√2))) −(1/(4(√2)))ln((1/(√2))−(1/2))](Q95463.png) | ||
| ||