
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 32041 by abdo imad last updated on 18/Mar/18
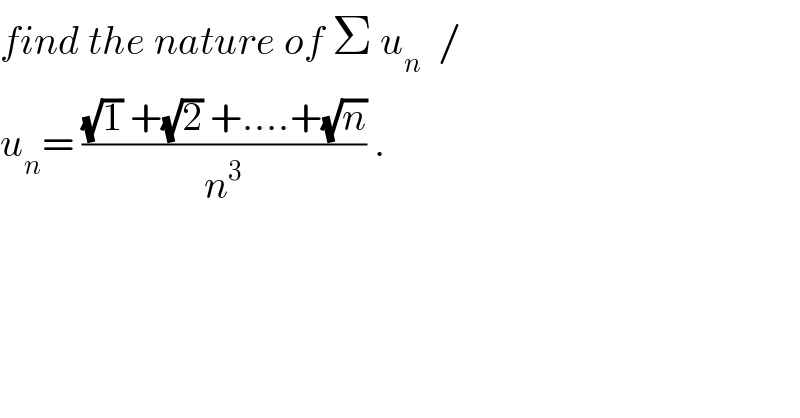
Commented by abdo imad last updated on 20/Mar/18
![we have u_n = (1/n^2 ) ( (1/(√n)) Σ_(k=1) ^n (√( (k/n))) ) =(1/(n(√n)))( (1/n) Σ_(k=1) ^n (√(k/n)) ) but lim_(n→∞) (1/n) Σ_(k=1) ^n (√(k/n)) = ∫_0 ^1 (√x) dx = [ (2/3) x^(3/2) ]_0 ^1 = (2/3) ⇒ u_n ∼ (2/(3n(√n))) and the serie Σ_(n≥1) (2/(3n(√n))) is convergent so Σ u_(n ) converges.](Q32122.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 32041 by abdo imad last updated on 18/Mar/18 | ||
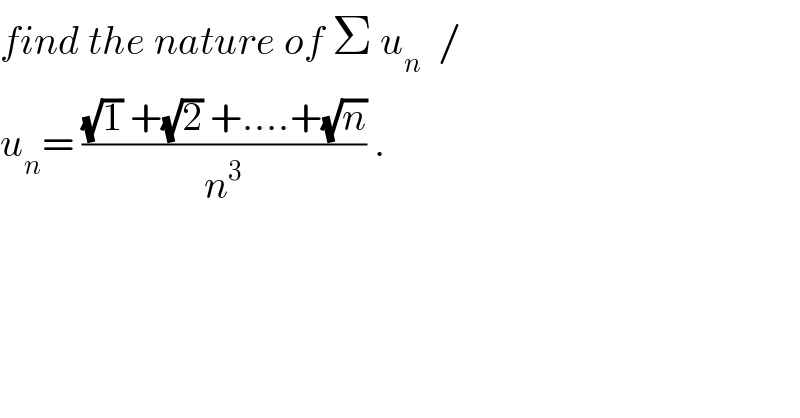 | ||
Commented by abdo imad last updated on 20/Mar/18 | ||
![we have u_n = (1/n^2 ) ( (1/(√n)) Σ_(k=1) ^n (√( (k/n))) ) =(1/(n(√n)))( (1/n) Σ_(k=1) ^n (√(k/n)) ) but lim_(n→∞) (1/n) Σ_(k=1) ^n (√(k/n)) = ∫_0 ^1 (√x) dx = [ (2/3) x^(3/2) ]_0 ^1 = (2/3) ⇒ u_n ∼ (2/(3n(√n))) and the serie Σ_(n≥1) (2/(3n(√n))) is convergent so Σ u_(n ) converges.](Q32122.png) | ||