Question and Answers Forum

All Questions      Topic List

Mechanics Questions

Previous in All Question      Next in All Question      

Previous in Mechanics      Next in Mechanics      

Question Number 32098 by Tinkutara last updated on 19/Mar/18

Commented by ajfour last updated on 19/Mar/18

$$\frac{3L}{4}.$$

Commented by Tinkutara last updated on 19/Mar/18

Yes correct. Did you use torque balancing or COM concept?

Commented by ajfour last updated on 19/Mar/18

$$comconcept.$$

Commented by mrW2 last updated on 19/Mar/18

$$whatis{x}_{max}ifyoucantakeasmany$$$$blocksasyoulike?$$

Commented by mrW2 last updated on 20/Mar/18

Commented by mrW2 last updated on 20/Mar/18

$$x_n=\frac{L}{2}(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n})$$$$\underset{n\to \mathrm{\infty }}{\lim }{x}_n=\mathrm{\infty }$$$$itmeanswithsufficientblocksone$$$$canreacheveryoverhang.$$

Commented by Tinkutara last updated on 20/Mar/18

@ajfour Sir please show COM concept. I can't solve by that method.

Commented by Tinkutara last updated on 20/Mar/18

$$@mrW2Sirhow$$$$\underset{n\to \mathrm{\infty }}{\lim }{x}_n=\mathrm{\infty }$$$$?$$

Commented by mrW2 last updated on 20/Mar/18

$$theharminicseriesisdivergent.$$$$x_{n+1}>x_n$$$$\Rightarrow \underset{n\to \mathrm{\infty }}{\lim }{x}_n=\mathrm{\infty }$$$$$$$$proof:$$$$assumeitconverges,i.e.$$$$S=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}....$$$$S>1+\frac{1}{2}+\frac{1}{4}+\frac{1}{4}+\frac{1}{6}+\frac{1}{6}....$$$$=\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{4}+\frac{1}{4}+\frac{1}{6}+\frac{1}{6}....$$$$=\frac{1}{2}+(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+....)$$$$\Rightarrow S>\frac{1}{2}+S$$$$thisiscontradiction.$$

Commented by Tinkutara last updated on 20/Mar/18

Thank you very much Sir! ��������

Commented by abdo imad last updated on 20/Mar/18

$$letput{H}_n=\sum _{k=1}^n\frac{1}{k}andprovethat{lim}_{n\to \mathrm{\infty }}{H}_n=+\mathrm{\infty }$$$$wehave{H}_n=1+\sum _{k=2}^n{\int }_{k-1}^k\frac{dt}{k}butk-1⩽t⩽k\Rightarrow$$$$\frac{1}{k}⩽\frac{1}{t}⩽\frac{1}{k-1}\Rightarrow \frac{1}{k}⩽{\int }_{k-1}^k\frac{dt}{t}⩽\frac{1}{k-1}\Rightarrow$$$$\sum _{k=2}^n\frac{1}{k}⩽\sum _{k=2}^n{\int }_{k-1}^k\frac{dt}{t}⩽\sum _{k=2}^n\frac{1}{k-1}\Rightarrow$$$$1+\sum _{k=2}^n\frac{1}{k}⩽1+\sum _{k=2}^n(ln\left(k\right)-ln(k-1))⩽1+\sum _{k=1}^{n-1}\frac{1}{k}\Rightarrow$$$$H_n⩽1+ln\left(n\right)⩽1+H_{n-1}\Rightarrow H_{n-1}⩾ln\left(n\right)\Rightarrow$$$$H_n⩾ln(n+1)\mathrm{\forall }n\in N^{★}but{lim}_{n\to \mathrm{\infty }}ln(n+1)=+\mathrm{\infty }\Rightarrow$$$${lim}_{n\to +\mathrm{\infty }}=+\mathrm{\infty }.alsowehavetherelation$$$$H_n-1⩽ln\left(n\right)⩽H_{n-1}forn⩾2.$$

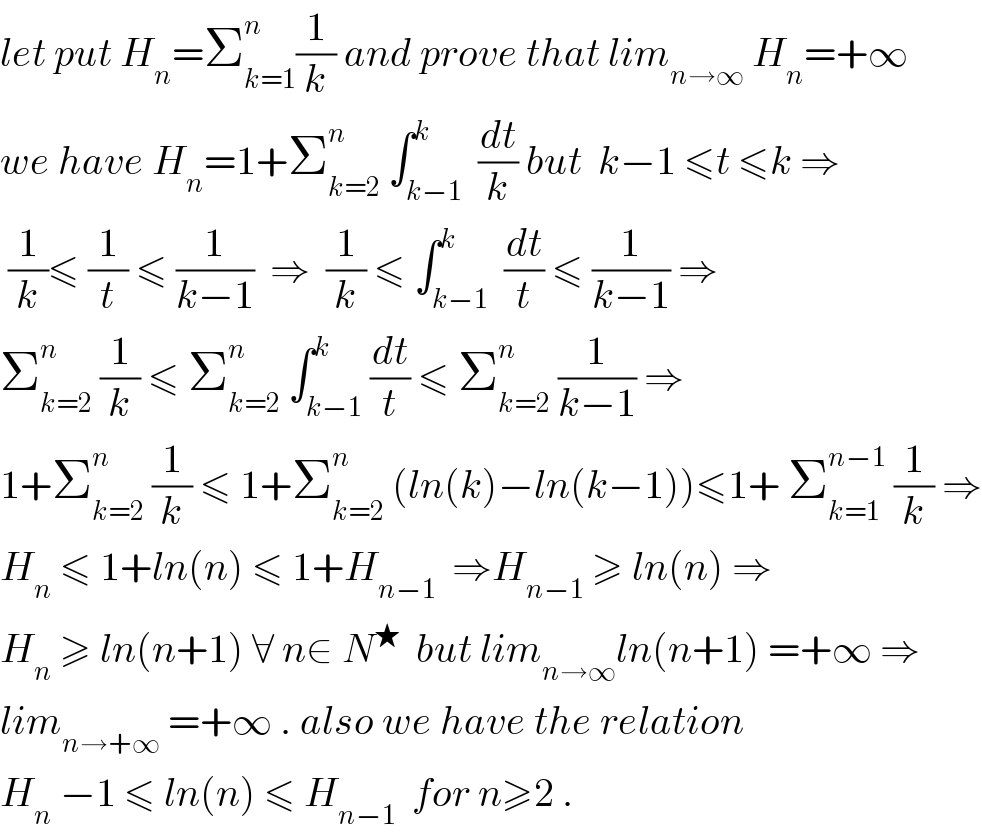
Commented by Tinkutara last updated on 21/Mar/18

Thank you abdo imad Sir!

Commented by abdo imad last updated on 21/Mar/18

$$nevermindsir$$

Commented by mrW2 last updated on 22/Mar/18

$$thanks!$$$$nicetoknow:$$$$\ln (n+1)<H_n<\ln \left(n\right)+1$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com