Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 32273 by abdo imad last updated on 22/Mar/18

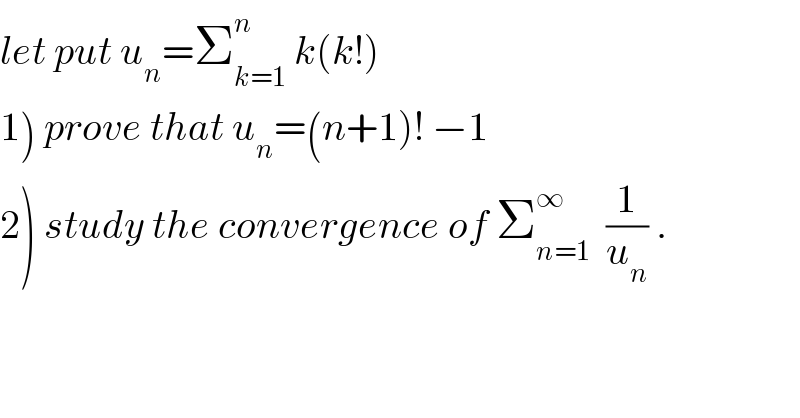
let put u_n =Σ_(k=1) ^n k(k!) 1) prove that u_n =(n+1)! −1 2) study the convergence of Σ_(n=1) ^∞ (1/u_n ) .

letputun=∑k=1nk(k!)1)provethatun=(n+1)!−12)studytheconvergenceof∑n=1∞1un.

Commented by abdo imad last updated on 25/Mar/18

1) let prove this relation by recurrence p(1) u_1 = 2!−1=1×(1!) p(1) is true let supose u_n =(n+1)!−1 ⇒u_(n+1) =Σ_(k=1) ^(n+1) k(k!) =Σ_(k=1) ^n k(k!) +(n+1)(n+1)! =(n+1)!−1 +(n+1)(n+1)!=(n+1)!(n+1+1) −1 =(n+2)(n+1)! −1 =(n+2)! −1 the implication p(n)⇒p(n+1) is true . 2)we have Σ_(n=1) ^∞ (1/u_n ) = Σ_(n=1) ^∞ (1/((n+1)! −1)) but for n→∞ (1/((n+1)! −1)) ∼ (1/((n+1)!)) and Σ (1/((n+1)!)) is convergent so Σ(1/u_n ) is covergent .

1)letprovethisrelationbyrecurrencep(1)u1=2!−1=1×(1!)p(1)istrueletsuposeun=(n+1)!−1⇒un+1=∑k=1n+1k(k!)=∑k=1nk(k!)+(n+1)(n+1)!=(n+1)!−1+(n+1)(n+1)!=(n+1)!(n+1+1)−1=(n+2)(n+1)!−1=(n+2)!−1theimplicationp(n)⇒p(n+1)istrue.2)wehave∑n=1∞1un=∑n=1∞1(n+1)!−1butforn→∞1(n+1)!−1∼1(n+1)!andΣ1(n+1)!isconvergentsoΣ1uniscovergent.

Answered by Tinkutara last updated on 23/Mar/18

u_n =Σ_(k=1) ^n (k+1−1)(k!) u_n =Σ_(k=1) ^n [(k+1)!−k!] It telescopes and becomes u_n =(n+1)!−1

un=∑nk=1(k+1−1)(k!)un=∑nk=1[(k+1)!−k!]Ittelescopesandbecomesun=(n+1)!−1

Terms of Service

Privacy Policy

Contact: info@tinkutara.com