Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 3228 by Rasheed Soomro last updated on 08/Dec/15

Why is circumference of a circle derivative of its area? (d/dr)(πr^2 )=2πr=circumference.

$$\mathcal{W}{hy}\:{is}\:{circumference}\:{of}\:{a}\:{circle}\:{derivative}\:{of} \\ $$$${its}\:{area}? \\ $$$$\frac{{d}}{{dr}}\left(\pi{r}^{\mathrm{2}} \right)=\mathrm{2}\pi{r}={circumference}. \\ $$

Commented by 123456 last updated on 08/Dec/15

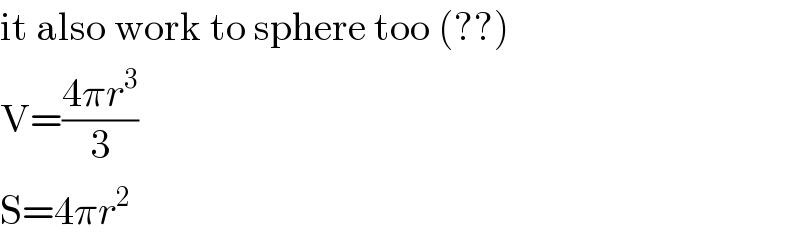
it also work to sphere too (??) V=((4πr^3 )/3) S=4πr^2

$$\mathrm{it}\:\mathrm{also}\:\mathrm{work}\:\mathrm{to}\:\mathrm{sphere}\:\mathrm{too}\:\left(??\right) \\ $$$$\mathrm{V}=\frac{\mathrm{4}\pi{r}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\mathrm{S}=\mathrm{4}\pi{r}^{\mathrm{2}} \\ $$

Commented by prakash jain last updated on 08/Dec/15

May be it has to with formula related to miximum area/volume given perimeter/area.

$$\mathrm{May}\:\mathrm{be}\:\mathrm{it}\:\mathrm{has}\:\mathrm{to}\:\mathrm{with}\:\mathrm{formula}\:\mathrm{related}\:\mathrm{to} \\ $$$$\mathrm{miximum}\:\mathrm{area}/\mathrm{volume}\:\mathrm{given}\:\mathrm{perimeter}/\mathrm{area}. \\ $$

Commented by 123456 last updated on 08/Dec/15

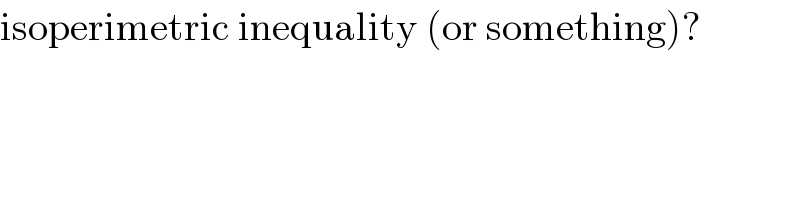
isoperimetric inequality (or something)?

$$\mathrm{isoperimetric}\:\mathrm{inequality}\:\left(\mathrm{or}\:\mathrm{something}\right)? \\ $$

Commented by Filup last updated on 08/Dec/15

Reversing the question, you get: Why is the area the integral of its circumferance? The circumferance, or locus, follows: x^2 +y^2 =r^2 The area of a full circle is then given by: A=2∫_(−r) ^( r) (√(r^2 −x^2 ))dx=πr^2

$$\mathrm{Reversing}\:\mathrm{the}\:\mathrm{question},\:\mathrm{you}\:\mathrm{get}: \\ $$$$\mathrm{Why}\:\mathrm{is}\:\mathrm{the}\:\mathrm{area}\:\mathrm{the}\:\mathrm{integral}\:\mathrm{of}\:\mathrm{its} \\ $$$$\mathrm{circumferance}? \\ $$$$ \\ $$$$\mathrm{The}\:\mathrm{circumferance},\:{or}\:{locus},\:\mathrm{follows}: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{a}\:\mathrm{full}\:\mathrm{circle}\:\mathrm{is}\:\mathrm{then}\:\mathrm{given}\:\mathrm{by}: \\ $$$${A}=\mathrm{2}\int_{−{r}} ^{\:{r}} \sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}=\pi{r}^{\mathrm{2}} \\ $$

Commented by Rasheed Soomro last updated on 08/Dec/15

Circumference here is measure of circle(locus) not circle itself. You have meant by circumference locus(circle) itself.

$$\:\mathcal{C}{ircumference}\:{here}\:{is}\:{measure}\:{of}\:{circle}\left({locus}\right)\:{not}\: \\ $$$${circle}\:{itself}. \\ $$$$\mathcal{Y}{ou}\:{have}\:{meant}\:{by}\:{circumference}\:{locus}\left({circle}\right) \\ $$$${itself}. \\ $$

Commented by Filup last updated on 08/Dec/15

i see

$${i}\:{see} \\ $$

Commented by Yozzi last updated on 08/Dec/15

It would appear to me that there exists a dimensional interpretation of the derivative/anti−derivative of certain physical equations. So that, in defining a circle by a quantity in its highest possible dimension in 2D−space (area), the derivative yields a 1D−space property of the circle−the length of the line which constitutes the circle.If we go further, 2π then represents a point if we perhaps decided to plot points P(r,(d^n A/dr^n )) in the plane, knowing the locus of a circle having area A and radius r. So, P(r,(d^0 A/dr^0 )) gives a shaded circle of radius r; P(r,(dA/dr)) gives a plain circle of radius r; P(r,(d^2 A/dr^2 )) gives a point and P(r,(d^3 A/dr^3 )) degenerates the circle completely. (This is just my view: it′s probably wrong.)

$${It}\:{would}\:{appear}\:{to}\:{me}\:{that}\:{there}\:{exists} \\ $$$${a}\:{dimensional}\:{interpretation}\:{of}\:{the} \\ $$$${derivative}/{anti}−{derivative}\:{of}\: \\ $$$${certain}\:{physical}\:{equations}.\: \\ $$$${So}\:{that},\:{in}\:{defining}\:{a}\:{circle}\:{by} \\ $$$${a}\:{quantity}\:{in}\:{its}\:{highest}\:{possible} \\ $$$${dimension}\:{in}\:\mathrm{2}{D}−{space}\:\left({area}\right),\:{the}\: \\ $$$${derivative}\:{yields}\:{a}\:\mathrm{1}{D}−{space}\:{property} \\ $$$${of}\:{the}\:{circle}−{the}\:{length}\:{of}\:{the}\:{line} \\ $$$${which}\:{constitutes}\:{the}\:{circle}.{If}\:{we} \\ $$$${go}\:{further},\:\mathrm{2}\pi\:{then}\:{represents}\:{a} \\ $$$${point}\:{if}\:{we}\:{perhaps}\:{decided}\:{to}\:{plot} \\ $$$${points}\:{P}\left({r},\frac{{d}^{{n}} {A}}{{dr}^{{n}} }\right)\:{in}\:{the}\:{plane},\:{knowing} \\ $$$${the}\:{locus}\:{of}\:{a}\:{circle}\:{having}\:{area}\:{A} \\ $$$${and}\:{radius}\:{r}.\:{So},\:{P}\left({r},\frac{{d}^{\mathrm{0}} {A}}{{dr}^{\mathrm{0}} }\right)\:{gives}\:{a} \\ $$$${shaded}\:{circle}\:{of}\:{radius}\:{r};\:{P}\left({r},\frac{{dA}}{{dr}}\right)\:{gives}\:{a}\:{plain} \\ $$$${circle}\:{of}\:{radius}\:{r};\:{P}\left({r},\frac{{d}^{\mathrm{2}} {A}}{{dr}^{\mathrm{2}} }\right)\:{gives} \\ $$$${a}\:{point}\:{and}\:{P}\left({r},\frac{{d}^{\mathrm{3}} {A}}{{dr}^{\mathrm{3}} }\right)\:{degenerates} \\ $$$${the}\:{circle}\:{completely}. \\ $$$$ \\ $$$$\left({This}\:{is}\:{just}\:{my}\:{view}:\:{it}'{s}\:{probably}\right. \\ $$$$\left.{wrong}.\right) \\ $$

Answered by prakash jain last updated on 08/Dec/15

Let us say we try to find out how much such curve exists. By the problem definition y=f(r,x). where r is an independent parameter. Length of a curve L(r) =∫_0 ^( r) (√(1+f_x (r,x)^2 ))dx Area of curve A(r)= ∫_0 ^( r) f(r,x)dx The problem statement is find all f(r,x) such that L(r)=(d/dr)A(r) ∫_0 ^( r) (√(1+f_x (r,x)^2 ))dx=(d/dr) ∫_0 ^( r) f(r,x)dx ∫_0 ^( r) (√(1+f_x (r,x)^2 ))dx=f(r,r)+∫_0 ^( r) f_r (r,x)dx ...(A) So we need to solve the above equation to find f(r,x). f(r,x)=(√(r^2 −x^2 )) satisfied (√(1+f_x (r,x)^2 ))=(√(1+(x^2 /(r^2 −x^2 ))))=(√(r^2 /(r^2 −x^2 )))=(r/(√(r^2 −x^2 ))) f_r (r,x)=(r/(√(r^2 −x^2 ))), f(r,r)=0 I will try to find more solution for A.

$$\mathrm{Let}\:\mathrm{us}\:\mathrm{say}\:\mathrm{we}\:\mathrm{try}\:\mathrm{to}\:\mathrm{find}\:\mathrm{out}\:\mathrm{how} \\ $$$$\mathrm{much}\:\mathrm{such}\:\mathrm{curve}\:\mathrm{exists}.\:\mathrm{By}\:\mathrm{the}\:\mathrm{problem} \\ $$$$\mathrm{definition}\:{y}={f}\left({r},{x}\right).\:{where}\:{r}\:{is}\:{an} \\ $$$${independent}\:{parameter}. \\ $$$$\mathrm{Length}\:\mathrm{of}\:\mathrm{a}\:\mathrm{curve}\:\mathrm{L}\left({r}\right)\:=\int_{\mathrm{0}} ^{\:\:{r}} \sqrt{\mathrm{1}+{f}_{{x}} \left({r},{x}\right)^{\mathrm{2}} \:}{dx} \\ $$$${A}\mathrm{rea}\:\mathrm{of}\:\mathrm{curve}\:\mathrm{A}\left({r}\right)=\:\int_{\mathrm{0}} ^{\:{r}} \:{f}\left({r},{x}\right){dx} \\ $$$$\mathrm{The}\:\mathrm{problem}\:\mathrm{statement}\:\mathrm{is}\:\mathrm{find}\:\mathrm{all} \\ $$$${f}\left({r},{x}\right)\:{such}\:{that}\:\mathrm{L}\left({r}\right)=\frac{{d}}{{dr}}{A}\left({r}\right) \\ $$$$\int_{\mathrm{0}} ^{\:{r}} \sqrt{\mathrm{1}+{f}_{{x}} \left({r},{x}\right)^{\mathrm{2}} \:}{dx}=\frac{{d}}{{dr}}\:\int_{\mathrm{0}} ^{\:{r}} \:{f}\left({r},{x}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\:{r}} \sqrt{\mathrm{1}+{f}_{{x}} \left({r},{x}\right)^{\mathrm{2}} \:}{dx}={f}\left({r},{r}\right)+\int_{\mathrm{0}} ^{\:{r}} {f}_{{r}} \left({r},{x}\right){dx}\:\:...\left({A}\right) \\ $$$$\mathrm{So}\:\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{above}\:\mathrm{equation}\:\mathrm{to} \\ $$$$\mathrm{find}\:{f}\left({r},{x}\right). \\ $$$${f}\left({r},{x}\right)=\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:{satisfied} \\ $$$$\sqrt{\mathrm{1}+{f}_{{x}} \left({r},{x}\right)^{\mathrm{2}} }=\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }}=\sqrt{\frac{{r}^{\mathrm{2}} }{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }}=\frac{{r}}{\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }} \\ $$$${f}_{{r}} \left({r},{x}\right)=\frac{{r}}{\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }},\:{f}\left({r},{r}\right)=\mathrm{0} \\ $$$$\mathrm{I}\:\mathrm{will}\:\mathrm{try}\:\mathrm{to}\:\mathrm{find}\:\mathrm{more}\:\mathrm{solution}\:\mathrm{for}\:{A}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com