Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 32295 by abdo imad last updated on 22/Mar/18

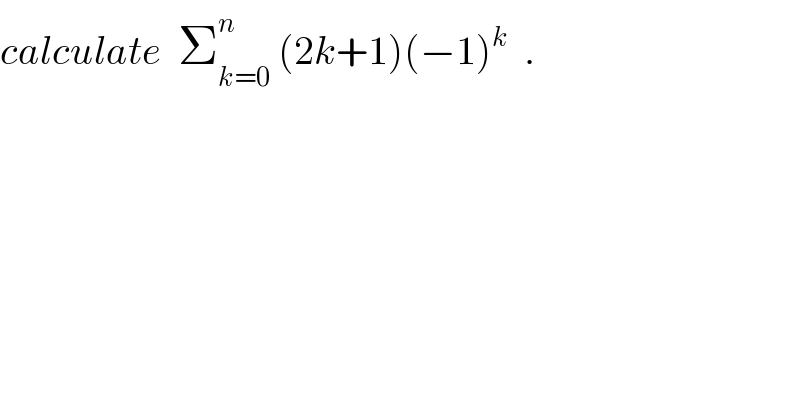
calculate Σ_(k=0) ^n (2k+1)(−1)^k .

$${calculate}\:\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\left(\mathrm{2}{k}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{k}} \:\:. \\ $$

Commented by prof Abdo imad last updated on 04/Apr/18

let put S_n = Σ_(k=0) ^n (2k+1)(−1)^k =Σ_(k=2p) (...) + Σ_(k=2p+1) (...) = Σ_(p=0) ^([(n/2)]) (4p+1) −Σ_(p=0) ^([((n−1)/2)]) (4p+3) but the sequences (4p+1) and (4p+3) are arithmetic Σ_(p=0) ^([(n/2)]) (4p+1) = (([(n/2)] +1)/2)( 1 + 4[(n/2)] +1) =(1+[(n/2)])( 1+2[(n/2)]) Σ_(p=0) ^([((n−1)/2)]) (4p+3) = (([((n−1)/2)] +1)/2)( 3 +4[((n−1)/2)] +3 ) = (1 +[((n−1)/2)])( 3 +2[((n−1)/2)])

$${let}\:{put}\:{S}_{{n}} =\:\sum_{{k}=\mathrm{0}} ^{{n}} \left(\mathrm{2}{k}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{k}} \\ $$$$=\sum_{{k}=\mathrm{2}{p}} \left(...\right)\:+\:\sum_{{k}=\mathrm{2}{p}+\mathrm{1}} \:\left(...\right) \\ $$$$=\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\left(\mathrm{4}{p}+\mathrm{1}\right)\:\:−\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\:\left(\mathrm{4}{p}+\mathrm{3}\right) \\ $$$${but}\:{the}\:{sequences}\:\left(\mathrm{4}{p}+\mathrm{1}\right)\:{and}\:\left(\mathrm{4}{p}+\mathrm{3}\right)\:{are}\:{arithmetic} \\ $$$$\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\left(\mathrm{4}{p}+\mathrm{1}\right)\:=\:\frac{\left[\frac{{n}}{\mathrm{2}}\right]\:+\mathrm{1}}{\mathrm{2}}\left(\:\mathrm{1}\:+\:\mathrm{4}\left[\frac{{n}}{\mathrm{2}}\right]\:+\mathrm{1}\right) \\ $$$$=\left(\mathrm{1}+\left[\frac{{n}}{\mathrm{2}}\right]\right)\left(\:\mathrm{1}+\mathrm{2}\left[\frac{{n}}{\mathrm{2}}\right]\right) \\ $$$$\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\left(\mathrm{4}{p}+\mathrm{3}\right)\:=\:\frac{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]\:+\mathrm{1}}{\mathrm{2}}\left(\:\mathrm{3}\:\:+\mathrm{4}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]\:+\mathrm{3}\:\right) \\ $$$$=\:\left(\mathrm{1}\:+\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]\right)\left(\:\mathrm{3}\:\:+\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]\right) \\ $$

Commented by prof Abdo imad last updated on 06/Apr/18

another method S_n = 2 Σ_(k=0) ^n k(−1)^k +Σ_(k=0) ^n (−1)^k but Σ_(k=0) ^n (−1)^k =((1−(−1)^(n+1) )/2) = ((1+(−1)^n )/2) Σ_(k=0) ^n k(−1)^k = −Σ_(k=1) ^n k(−1)^(k−1) for that let find Σ_(k=1) ^n k x^(k−1) we have for x≠1 Σ_(k=0) ^n x^k = ((x^(n+1) −1)/(x−1)) by derivation we get Σ_(k=1) ^n k x^(k−1) = ((nx^(n+1) −(n+1)x^n +1)/((x−1)^2 )) ⇒ Σ_(k=1) ^n k (−1)^(k−1) = ((n(−1)^(n+1) −(n+1)(−1)^n +1)/4) = ((1−(2n+1)(−1)^n )/4) ⇒ S_n = ((1+(−1)^n )/2) + ((1−(2n+1)(−1)^n )/4) .

$${another}\:{method} \\ $$$${S}_{{n}} =\:\mathrm{2}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{k}\left(−\mathrm{1}\right)^{{k}} \:\:+\sum_{{k}=\mathrm{0}} ^{{n}} \:\left(−\mathrm{1}\right)^{{k}} \:{but} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:\left(−\mathrm{1}\right)^{{k}} \:=\frac{\mathrm{1}−\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{2}}\:=\:\frac{\mathrm{1}+\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{k}\left(−\mathrm{1}\right)^{{k}} \:=\:−\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \:{for}\:{that}\:{let} \\ $$$${find}\:\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}\:{x}^{{k}−\mathrm{1}} \:\:{we}\:{have}\:{for}\:{x}\neq\mathrm{1} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{x}^{{k}} \:=\:\frac{{x}^{{n}+\mathrm{1}} \:−\mathrm{1}}{{x}−\mathrm{1}}\:\:{by}\:{derivation}\:{we}\:{get} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}\:{x}^{{k}−\mathrm{1}} \:\:=\:\frac{{nx}^{{n}+\mathrm{1}} \:−\left({n}+\mathrm{1}\right){x}^{{n}} \:+\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}\:\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \:=\:\frac{{n}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \:−\left({n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} \:+\mathrm{1}}{\mathrm{4}} \\ $$$$=\:\frac{\mathrm{1}−\left(\mathrm{2}{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}}\:\Rightarrow \\ $$$${S}_{{n}} \:=\:\:\frac{\mathrm{1}+\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}}\:\:+\:\frac{\mathrm{1}−\left(\mathrm{2}{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com