
Question and Answers Forum
Question Number 32305 by abdo imad last updated on 22/Mar/18
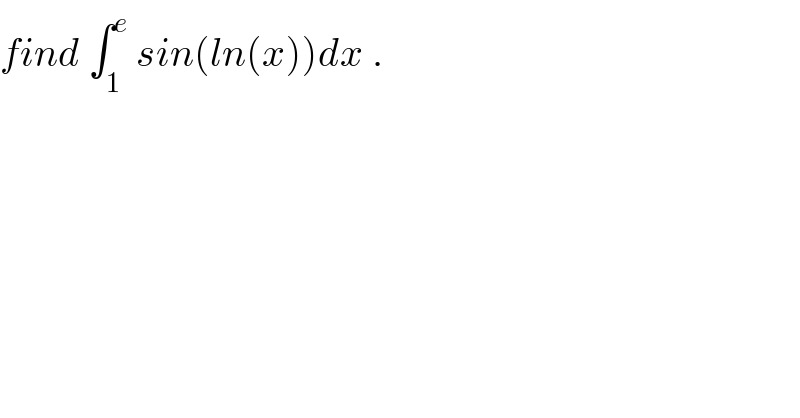
Commented by abdo imad last updated on 24/Mar/18
![let use the ch.lnx=t ⇒ I = ∫_0 ^1 sint e^t dt and I =Im (∫_0 ^1 e^(it +t) dt) =Im( ∫_0 ^1 e^((1+i)t) dt) but ∫_0 ^1 e^((1+i)t) dt = (1/(1+i))[ e^((1+i)t) ]_0 ^1 = (1/(1+i))( e^(1+i) −1) =((1−i)/2)( e( cos(1) +isin(1) −1) =((e cos(1) +ie sin(1) −1 −ie cos(1) +sin(1) +i)/2) =((e cos(1) +sin(1)−1 +i(e sin(1) −e cos(1) +1))/2) I = (1/2)( e sin(1)−e cos(1) +1) .](Q32411.png)
Answered by sma3l2996 last updated on 23/Mar/18
![u=sin(lnx)⇒u′=(1/x)cos(lnx) v′=1⇒v=x so ∫_1 ^e sin(lnx)dx=[xsin(lnx)]_1 ^e −∫_1 ^e cos(lnx)dx =esin(1)−∫_1 ^e cos(lnx)dx u=cos(lnx)⇒u′=−(1/x)sin(lnx) v′=1⇒v=x ∫_1 ^e sin(lnx)dx=e.sin(1)−[xcos(lnx)]_1 ^e −∫_1 ^e sin(lnx)dx 2∫_1 ^e sin(lnx)dx=e.sin(1)−e.cos(1)+1 ∫_1 ^e sin(lnx)dx=(e/2)(sin1−cos1)+(1/2)](Q32325.png)
Commented by abdo imad last updated on 24/Mar/18

| ||
Question and Answers Forum | ||
Question Number 32305 by abdo imad last updated on 22/Mar/18 | ||
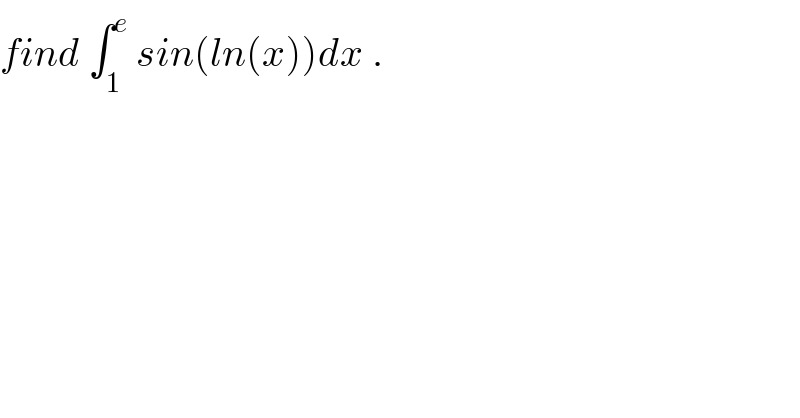 | ||
Commented by abdo imad last updated on 24/Mar/18 | ||
![let use the ch.lnx=t ⇒ I = ∫_0 ^1 sint e^t dt and I =Im (∫_0 ^1 e^(it +t) dt) =Im( ∫_0 ^1 e^((1+i)t) dt) but ∫_0 ^1 e^((1+i)t) dt = (1/(1+i))[ e^((1+i)t) ]_0 ^1 = (1/(1+i))( e^(1+i) −1) =((1−i)/2)( e( cos(1) +isin(1) −1) =((e cos(1) +ie sin(1) −1 −ie cos(1) +sin(1) +i)/2) =((e cos(1) +sin(1)−1 +i(e sin(1) −e cos(1) +1))/2) I = (1/2)( e sin(1)−e cos(1) +1) .](Q32411.png) | ||
Answered by sma3l2996 last updated on 23/Mar/18 | ||
![u=sin(lnx)⇒u′=(1/x)cos(lnx) v′=1⇒v=x so ∫_1 ^e sin(lnx)dx=[xsin(lnx)]_1 ^e −∫_1 ^e cos(lnx)dx =esin(1)−∫_1 ^e cos(lnx)dx u=cos(lnx)⇒u′=−(1/x)sin(lnx) v′=1⇒v=x ∫_1 ^e sin(lnx)dx=e.sin(1)−[xcos(lnx)]_1 ^e −∫_1 ^e sin(lnx)dx 2∫_1 ^e sin(lnx)dx=e.sin(1)−e.cos(1)+1 ∫_1 ^e sin(lnx)dx=(e/2)(sin1−cos1)+(1/2)](Q32325.png) | ||
| ||
Commented by abdo imad last updated on 24/Mar/18 | ||
 | ||