
Question Number 32312 by NECx last updated on 23/Mar/18

$${A}\:{small}\:{ball}\:{is}\:{dropped}\:{from}\:{a}\: \\ $$$${height}\:{of}\:\mathrm{1}{m}\:{into}\:{a}\:{horizontal} \\ $$$${floor}.{Each}\:{time}\:{it}\:{rebounces}\:{to} \\ $$$$\mathrm{3}/\mathrm{5}\:{of}\:{the}\:{height}\:{it}\:{has}\:{fallen}. \\ $$$$\left.{a}\right){show}\:{that}\:{when}\:{the}\:{ball}\:{strikes} \\ $$$${the}\:{ground}\:{for}\:{the}\:{third}\:{time}\:,{it} \\ $$$${has}\:{travelled}\:{a}\:{distance}\:{of}\:\mathrm{2}.\mathrm{92}{m} \\ $$$$\left.{b}\right){Show}\:{that}\:{the}\:{total}\:{distance} \\ $$$${travelled}\:{by}\:{the}\:{ball}\:{cant}\:{exceed} \\ $$$$\mathrm{4}{m}. \\ $$
Commented by NECx last updated on 23/Mar/18
$${please}\:{help}\:{with}\:{this} \\ $$
Answered by mrW2 last updated on 23/Mar/18
![1st strike: l_1 =1 2nd strike: l_2 =1+(3/5)×2 3rd strike: l_3 =1+(3/5)×2+((3/5))^2 ×2=2.92m .... n−th strike: l_n =1+(3/5)×2+((3/5))^2 ×2+...+((3/5))^(n−1) ×2 l_n =2[1+(3/5)+((3/5))^2 +...+((3/5))^(n−1) ]−1 lim_(n→∞) l_n =(2/(1−(3/5)))−1=4 m ⇒l_n <4 m](Q32370.png)
$$\mathrm{1}{st}\:{strike}:\:{l}_{\mathrm{1}} =\mathrm{1} \\ $$$$\mathrm{2}{nd}\:{strike}:\:{l}_{\mathrm{2}} =\mathrm{1}+\frac{\mathrm{3}}{\mathrm{5}}×\mathrm{2} \\ $$$$\mathrm{3}{rd}\:{strike}:\:{l}_{\mathrm{3}} =\mathrm{1}+\frac{\mathrm{3}}{\mathrm{5}}×\mathrm{2}+\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} ×\mathrm{2}=\mathrm{2}.\mathrm{92}{m} \\ $$$$.... \\ $$$${n}−{th}\:{strike}:\:{l}_{{n}} =\mathrm{1}+\frac{\mathrm{3}}{\mathrm{5}}×\mathrm{2}+\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} ×\mathrm{2}+...+\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{n}−\mathrm{1}} ×\mathrm{2} \\ $$$${l}_{{n}} =\mathrm{2}\left[\mathrm{1}+\frac{\mathrm{3}}{\mathrm{5}}+\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} +...+\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{n}−\mathrm{1}} \right]−\mathrm{1} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{l}_{{n}} =\frac{\mathrm{2}}{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{5}}}−\mathrm{1}=\mathrm{4}\:{m} \\ $$$$\Rightarrow{l}_{{n}} <\mathrm{4}\:{m} \\ $$
Commented by NECx last updated on 25/Mar/18

$${wow}.....\:{Thanks} \\ $$
Commented by NECx last updated on 25/Mar/18
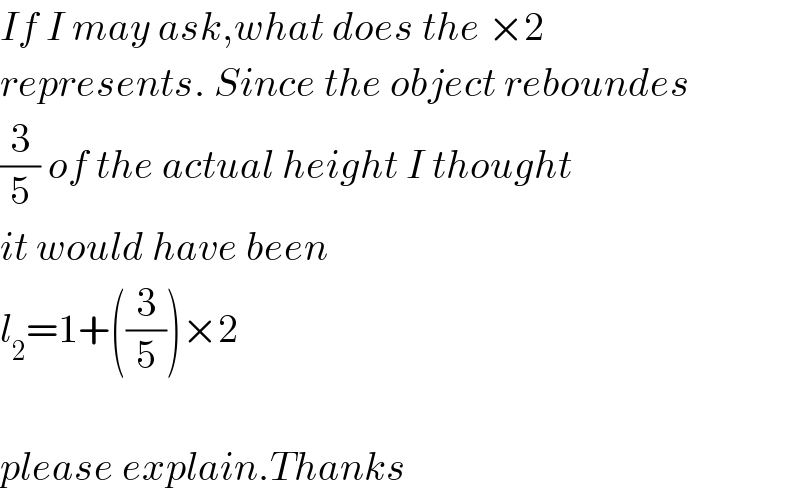
$${If}\:{I}\:{may}\:{ask},{what}\:{does}\:{the}\:×\mathrm{2} \\ $$$${represents}.\:{Since}\:{the}\:{object}\:{reboundes} \\ $$$$\frac{\mathrm{3}}{\mathrm{5}}\:{of}\:{the}\:{actual}\:{height}\:{I}\:{thought} \\ $$$${it}\:{would}\:{have}\:{been}\: \\ $$$${l}_{\mathrm{2}} =\mathrm{1}+\left(\frac{\mathrm{3}}{\mathrm{5}}\right)×\mathrm{2} \\ $$$$ \\ $$$${please}\:{explain}.{Thanks} \\ $$
Commented by mrW2 last updated on 06/Apr/18
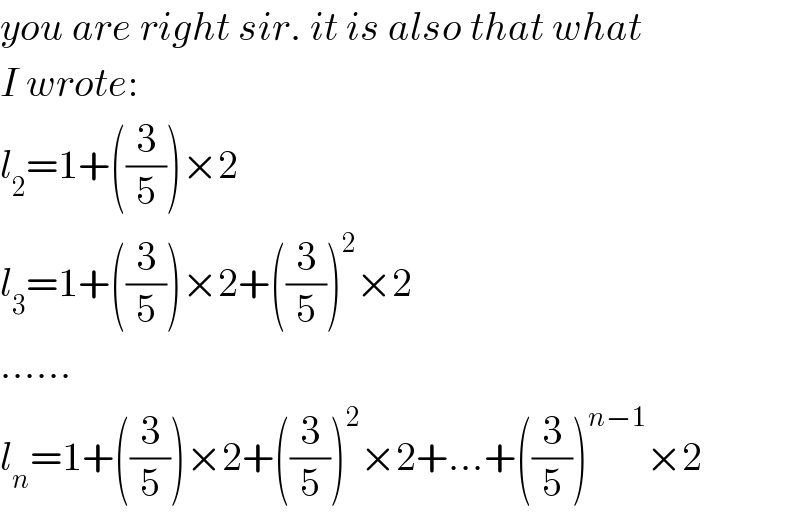
$${you}\:{are}\:{right}\:{sir}.\:{it}\:{is}\:{also}\:{that}\:{what} \\ $$$${I}\:{wrote}: \\ $$$${l}_{\mathrm{2}} =\mathrm{1}+\left(\frac{\mathrm{3}}{\mathrm{5}}\right)×\mathrm{2} \\ $$$${l}_{\mathrm{3}} =\mathrm{1}+\left(\frac{\mathrm{3}}{\mathrm{5}}\right)×\mathrm{2}+\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} ×\mathrm{2} \\ $$$$...... \\ $$$${l}_{{n}} =\mathrm{1}+\left(\frac{\mathrm{3}}{\mathrm{5}}\right)×\mathrm{2}+\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} ×\mathrm{2}+...+\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{n}−\mathrm{1}} ×\mathrm{2} \\ $$
