
Question and Answers Forum
Question Number 32330 by abdo imad last updated on 23/Mar/18
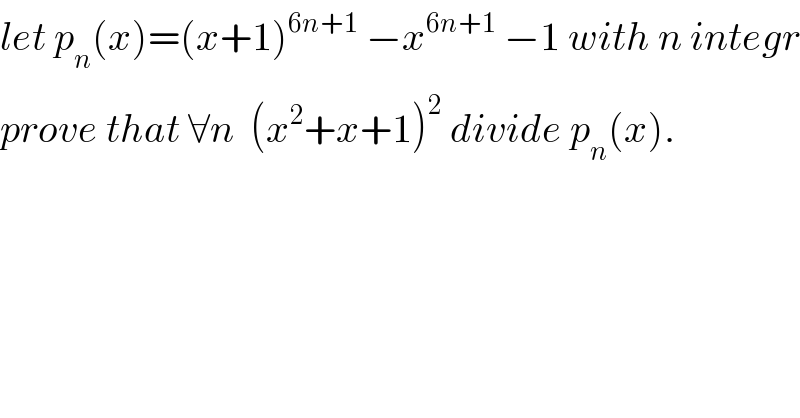
Commented by abdo imad last updated on 01/Apr/18
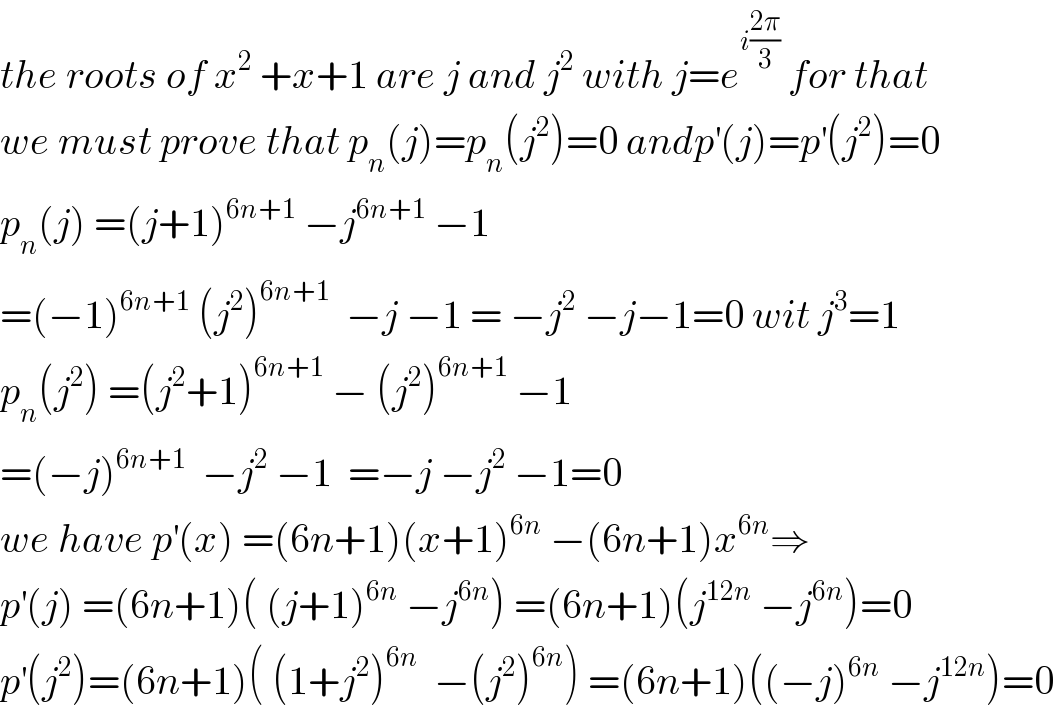
| ||
Question and Answers Forum | ||
Question Number 32330 by abdo imad last updated on 23/Mar/18 | ||
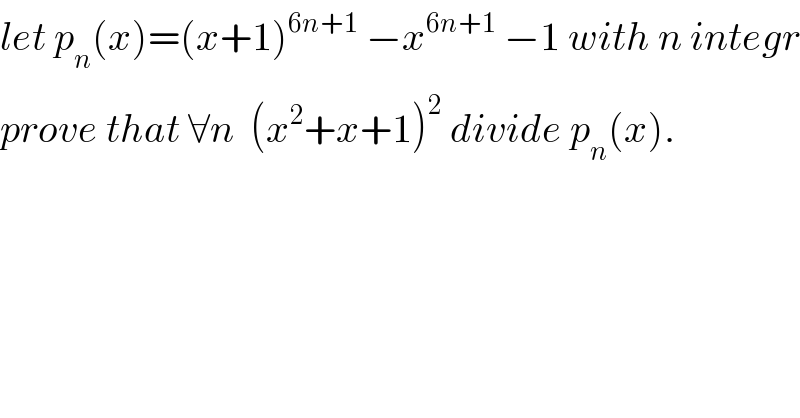 | ||
Commented by abdo imad last updated on 01/Apr/18 | ||
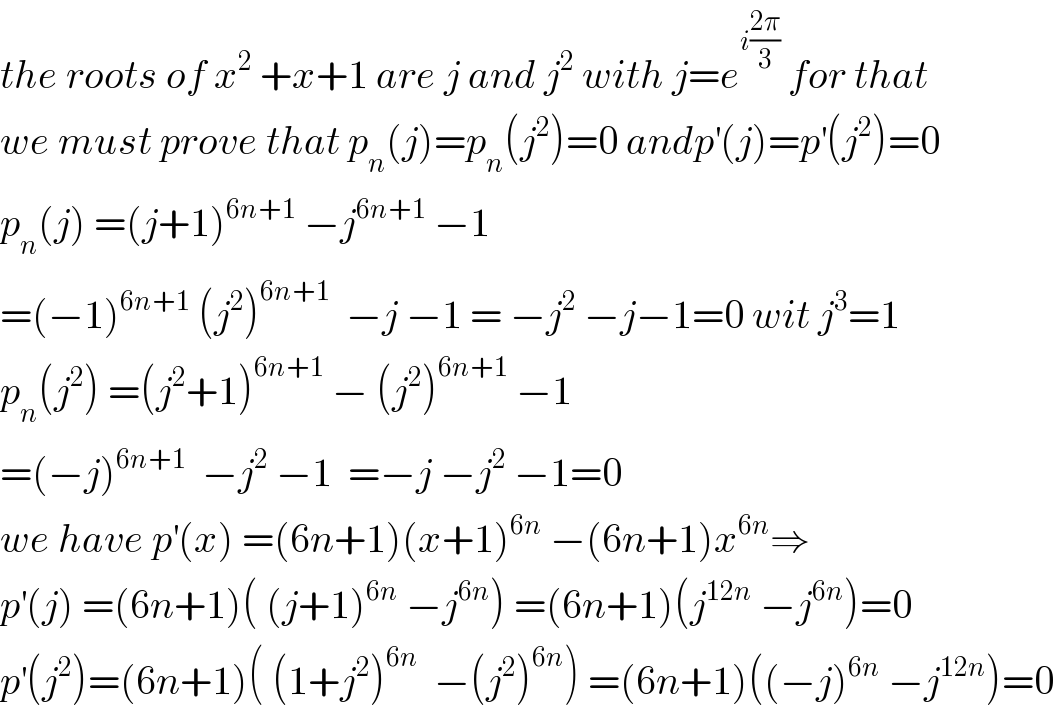 | ||