
Question and Answers Forum
Question Number 32339 by abdo imad last updated on 23/Mar/18
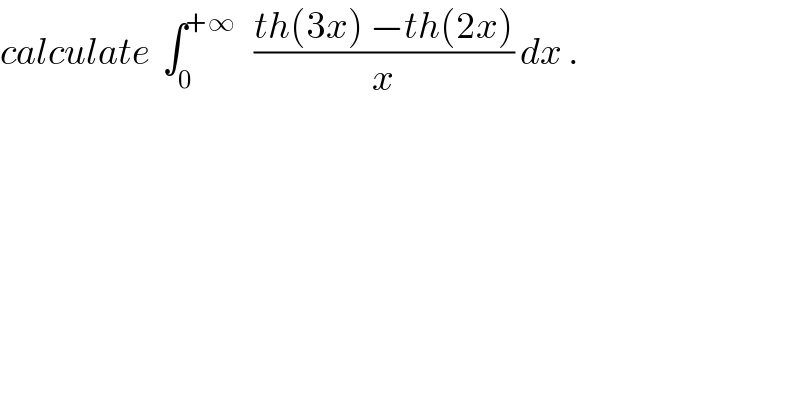
Commented by abdo imad last updated on 24/Mar/18
![I =lim _(ξ→+∞) I(ξ) with I(ξ) = ∫_0 ^(ξ ) ((th(3x)−th(2x))/x)dx I(ξ) = ∫_0 ^ξ ((th(3x))/x) dx −∫_0 ^ξ ((th(2x))/x)dx but ch.3x=t give ∫_0 ^ξ ((th(3x))/x)dx = ∫_0 ^(3ξ) ((th(t))/(t/3)) (dt/3) =∫_0 ^(3ξ) ((th(t))/t)dt also we have ∫_0 ^ξ ((th(2x))/x)dx = ∫_0 ^(2ξ) ((th(t))/t)dt ⇒ I(ξ) = ∫_0 ^(3ξ) ((th(t))/t)dt −∫_0 ^(2ξ) ((th(t))/t)dt =∫_(2ξ) ^(3ξ) ((th(t))/t)dt but ∃ c ∈]2ξ,3ξ[ / I(ξ) =th(c) ∫_(2ξ) ^(3ξ) (dt/t)=ln((3/2))th(c) ⇒ lim_(ξ→+∞) I(ξ) =ln(3)−ln(2) .( look that lim_(c→+∞) thc=1)](Q32434.png)
| ||
Question and Answers Forum | ||
Question Number 32339 by abdo imad last updated on 23/Mar/18 | ||
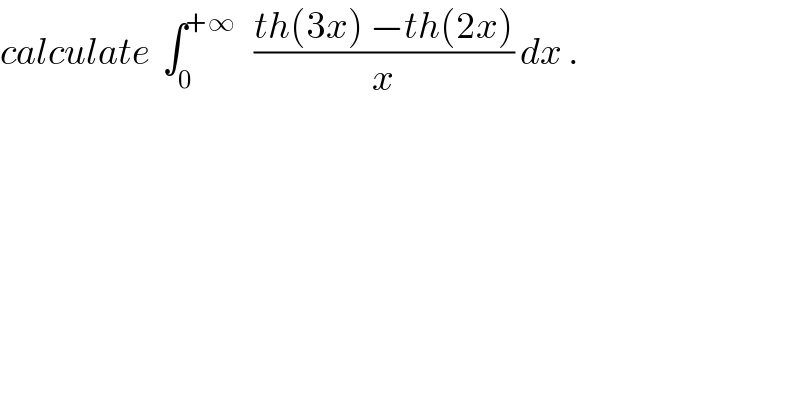 | ||
Commented by abdo imad last updated on 24/Mar/18 | ||
![I =lim _(ξ→+∞) I(ξ) with I(ξ) = ∫_0 ^(ξ ) ((th(3x)−th(2x))/x)dx I(ξ) = ∫_0 ^ξ ((th(3x))/x) dx −∫_0 ^ξ ((th(2x))/x)dx but ch.3x=t give ∫_0 ^ξ ((th(3x))/x)dx = ∫_0 ^(3ξ) ((th(t))/(t/3)) (dt/3) =∫_0 ^(3ξ) ((th(t))/t)dt also we have ∫_0 ^ξ ((th(2x))/x)dx = ∫_0 ^(2ξ) ((th(t))/t)dt ⇒ I(ξ) = ∫_0 ^(3ξ) ((th(t))/t)dt −∫_0 ^(2ξ) ((th(t))/t)dt =∫_(2ξ) ^(3ξ) ((th(t))/t)dt but ∃ c ∈]2ξ,3ξ[ / I(ξ) =th(c) ∫_(2ξ) ^(3ξ) (dt/t)=ln((3/2))th(c) ⇒ lim_(ξ→+∞) I(ξ) =ln(3)−ln(2) .( look that lim_(c→+∞) thc=1)](Q32434.png) | ||