
Question and Answers Forum
Question Number 32349 by abdo imad last updated on 23/Mar/18
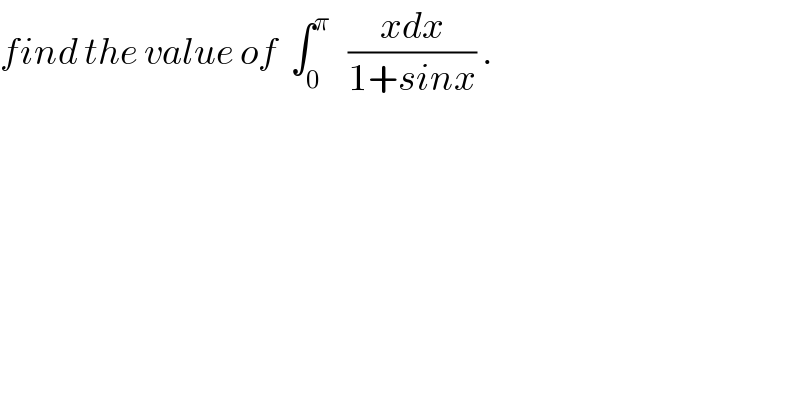
Commented by abdo imad last updated on 24/Mar/18
![the ch.tan((x/2))=t give I =∫_0 ^π ((xdx)/(1+sinx)) =∫_0 ^∞ ((2artant)/(1+((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) =4 ∫_0 ^∞ ((arctant)/(1+t^2 +2t))dt =4 ∫_0 ^∞ ((arctant)/((t+1)^2 ))dt ′by parts we get I =4( [−(1/(t+1)) arctant]_o ^(+∞) −∫_0 ^∞ −(1/(t+1)) (dt/(1+t^2 ))) I =4 ∫_0 ^∞ (dt/((t+1)(t^2 +1))) let decompose f(t) = (1/((t+1)(t^2 +1))) =(a/(t+1)) +((bt +c)/(t^2 +1)) a=lim_(t→−1) (t+1)f(t) =(1/2) lim_(t→+∞) tf(t) =0 =a +b ⇒b=−a=−(1/2) ⇒ f(t) = (1/(2(t+1))) +((((−1)/2)t +c)/(t^2 +1)) f(0) =1 = (1/2) +c ⇒ c=(1/2) ⇒f(t)= (1/(2(t+1))) +(1/2) ((−t +1)/(t^2 +1)) I = 2∫_0 ^∞ ( (1/(t+1)) −((t−1)/(t^2 +1)))dt =2∫_0 ^∞ ( (1/(t+1)) −(1/2) ((2t)/(t^2 +1)))dt +2 ∫_0 ^∞ (dt/(t^2 +1)) I = 2 [ln∣t+1∣−ln(√(t^2 +1)) ]_0 ^∞ +π I = 2 [ln∣ ((t+1)/(√(t^2 +1)))∣]_0 ^∞ +π =0+π ⇒ I =π .](Q32430.png)
| ||
Question and Answers Forum | ||
Question Number 32349 by abdo imad last updated on 23/Mar/18 | ||
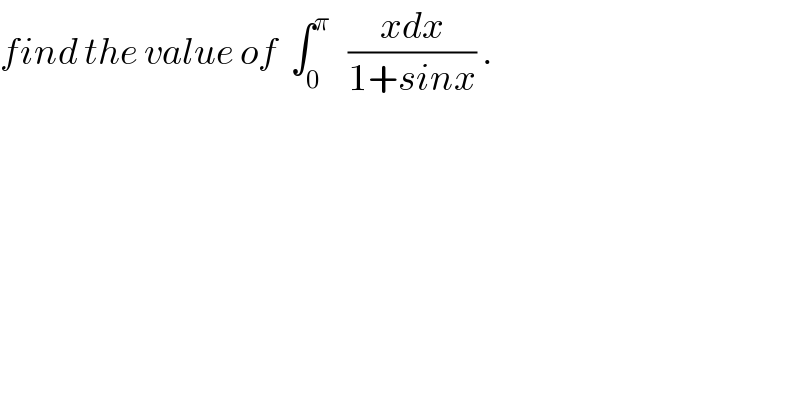 | ||
Commented by abdo imad last updated on 24/Mar/18 | ||
![the ch.tan((x/2))=t give I =∫_0 ^π ((xdx)/(1+sinx)) =∫_0 ^∞ ((2artant)/(1+((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) =4 ∫_0 ^∞ ((arctant)/(1+t^2 +2t))dt =4 ∫_0 ^∞ ((arctant)/((t+1)^2 ))dt ′by parts we get I =4( [−(1/(t+1)) arctant]_o ^(+∞) −∫_0 ^∞ −(1/(t+1)) (dt/(1+t^2 ))) I =4 ∫_0 ^∞ (dt/((t+1)(t^2 +1))) let decompose f(t) = (1/((t+1)(t^2 +1))) =(a/(t+1)) +((bt +c)/(t^2 +1)) a=lim_(t→−1) (t+1)f(t) =(1/2) lim_(t→+∞) tf(t) =0 =a +b ⇒b=−a=−(1/2) ⇒ f(t) = (1/(2(t+1))) +((((−1)/2)t +c)/(t^2 +1)) f(0) =1 = (1/2) +c ⇒ c=(1/2) ⇒f(t)= (1/(2(t+1))) +(1/2) ((−t +1)/(t^2 +1)) I = 2∫_0 ^∞ ( (1/(t+1)) −((t−1)/(t^2 +1)))dt =2∫_0 ^∞ ( (1/(t+1)) −(1/2) ((2t)/(t^2 +1)))dt +2 ∫_0 ^∞ (dt/(t^2 +1)) I = 2 [ln∣t+1∣−ln(√(t^2 +1)) ]_0 ^∞ +π I = 2 [ln∣ ((t+1)/(√(t^2 +1)))∣]_0 ^∞ +π =0+π ⇒ I =π .](Q32430.png) | ||