
Question and Answers Forum
Question Number 32351 by abdo imad last updated on 23/Mar/18
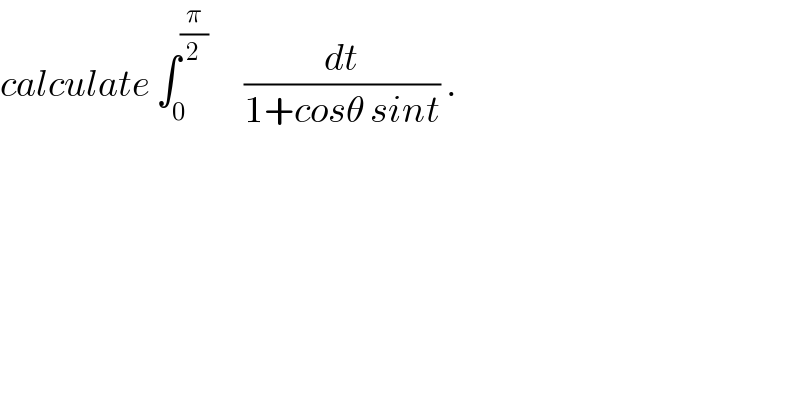
Answered by sma3l2996 last updated on 25/Mar/18
![let x=tan(t/2)⇒dt=((2dx)/(1+x^2 )) sint=((2x)/(1+x^2 )) ∫_0 ^(π/2) (dt/(1+cosθsint))=2∫_0 ^1 (dx/(1+x^2 +2xcosθ))=2∫_0 ^1 (dx/((x+cosθ)^2 +sin^2 θ)) =(2/(sin^2 θ))∫_0 ^1 (dx/((((x+cosθ)/(sinθ)))^2 +1)) let u=((x+cosθ)/(sinθ))⇒dx=sinθdu ∫_0 ^(π/2) (dt/(1+cosθsint))=(2/(sinθ))∫_(cotθ) ^((1+cosθ)/(sinθ)) (du/(u^2 +1))=(2/(sinθ))[arctan(((x+cosθ)/(sinθ)))]_0 ^1 =(2/(sinθ))(arctan(((1+cosθ)/(sinθ)))−arctan(cotθ))](Q32468.png)
| ||
Question and Answers Forum | ||
Question Number 32351 by abdo imad last updated on 23/Mar/18 | ||
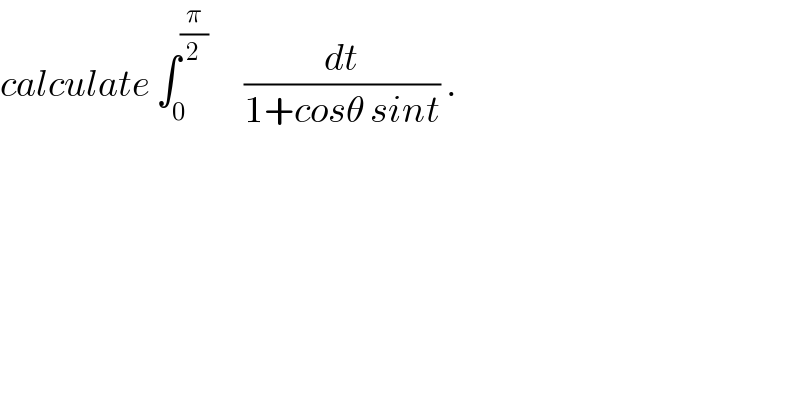 | ||
Answered by sma3l2996 last updated on 25/Mar/18 | ||
![let x=tan(t/2)⇒dt=((2dx)/(1+x^2 )) sint=((2x)/(1+x^2 )) ∫_0 ^(π/2) (dt/(1+cosθsint))=2∫_0 ^1 (dx/(1+x^2 +2xcosθ))=2∫_0 ^1 (dx/((x+cosθ)^2 +sin^2 θ)) =(2/(sin^2 θ))∫_0 ^1 (dx/((((x+cosθ)/(sinθ)))^2 +1)) let u=((x+cosθ)/(sinθ))⇒dx=sinθdu ∫_0 ^(π/2) (dt/(1+cosθsint))=(2/(sinθ))∫_(cotθ) ^((1+cosθ)/(sinθ)) (du/(u^2 +1))=(2/(sinθ))[arctan(((x+cosθ)/(sinθ)))]_0 ^1 =(2/(sinθ))(arctan(((1+cosθ)/(sinθ)))−arctan(cotθ))](Q32468.png) | ||
| ||