If the equation ax^2 +2bx−3c=0 has no real roots and (((3c)/4))< a+b, then


Question and Answers Forum

All Questions Topic List
UNKNOWN Questions
Previous in All Question Next in All Question
Previous in UNKNOWN Next in UNKNOWN
Question Number 32382 by hizmzm1 last updated on 24/Mar/18

$If the equation {a x}^{2} + 2 b x - 3 c = 0 has$ $no real roots and (\frac{3 c}{4}) < a + b, then$
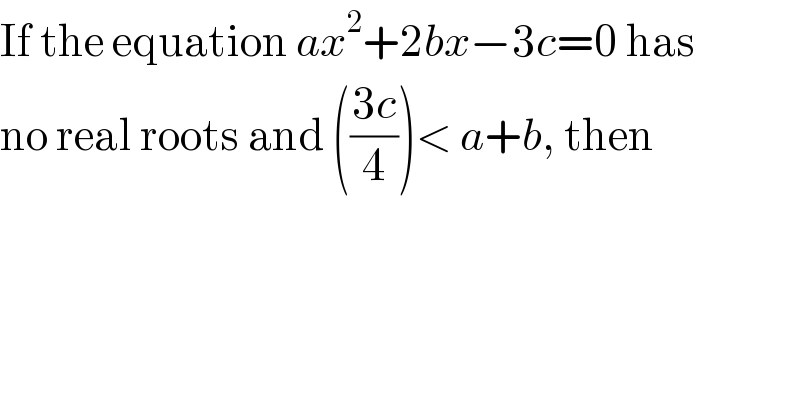
Commented byMJS last updated on 24/Mar/18

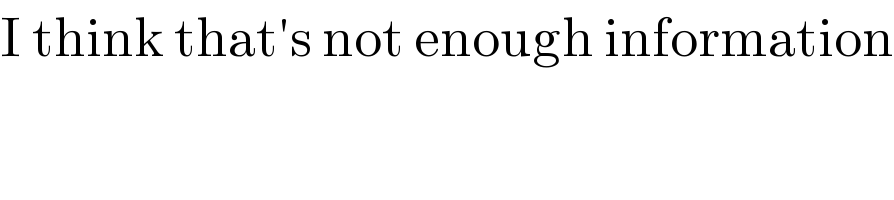
$I think {that}^{'} s not enough information$
Commented byMJS last updated on 24/Mar/18

$x^{2} + \frac{2 b}{a} x - \frac{3 c}{a} = 0$ $exactly one root :$ ${(x - r)}^{2} = x^{2} + \frac{2 b}{a} x - \frac{3 c}{a}$ $I . - 2 r = \frac{2 b}{a} \Rightarrow r^{2} = \frac{b^{2}}{a^{2}}$ $II . r^{2} = - \frac{3 c}{a}$ $\Rightarrow - \frac{3 c}{a} = \frac{b^{2}}{a^{2}} \Rightarrow c = - \frac{b^{2}}{3 a}$ $but now we have 1 root . It$ $disappears when we add a$ $real number > 0 \Rightarrow$ $\Rightarrow c > - \frac{b^{2}}{3 a}$ $\frac{3 c}{4} < a + b \Rightarrow c < \frac{4}{3} (a + b)$ $- \frac{b^{2}}{3 a} < c < \frac{4}{3} (a + b)$ $[\Rightarrow - \frac{b^{2}}{3 a} < \frac{4}{3} (a + b)$ $case 1 : a < 0$ $- b^{2} > 4 a (a + b)$ $- 4 a^{2} - 4 a b - b^{2} > 0$ $4 a^{2} + 4 a b + b^{2} < 0$ ${(2 a + b)}^{2} < 0 \Rightarrow no solution$ $case 2 : a > 0 leads to$ ${(2 a + b)}^{2} > 0$ $\Rightarrow a > 0]$
	Answered by Joel578 last updated on 24/Mar/18

	$no real roots \to D < 0$ ${(2 b)}^{2} - 4 a (- 3 c) < 0$ $4 b^{2} + 12 a c < 0$ $b^{2} > 3 a c$ $3 c < 4 (a + b)$ $3 a c < 4 a^{2} + 4 a b$ $3 a c < b^{2}$
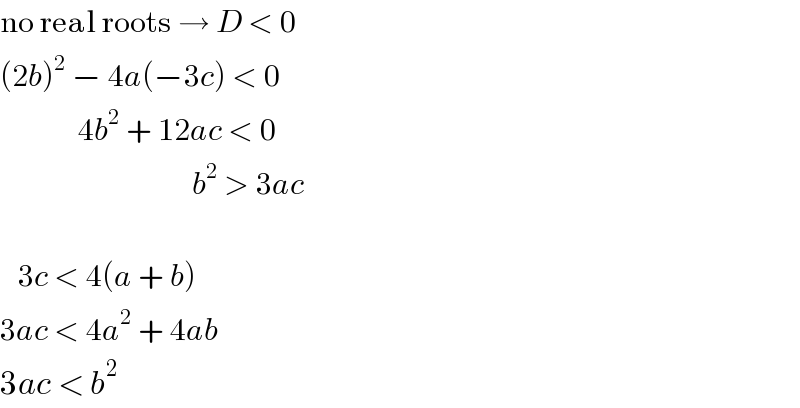
	Commented byMJS last updated on 24/Mar/18

	$3 c < 4 (a + b) \Rightarrow 3 a c < 4 a^{2} + 4 a b with a > 0$ $3 c > 4 (a + b) \Rightarrow 3 a c > 4 a^{2} + 4 a b with a < 0$ $can you show a > 0 ?$
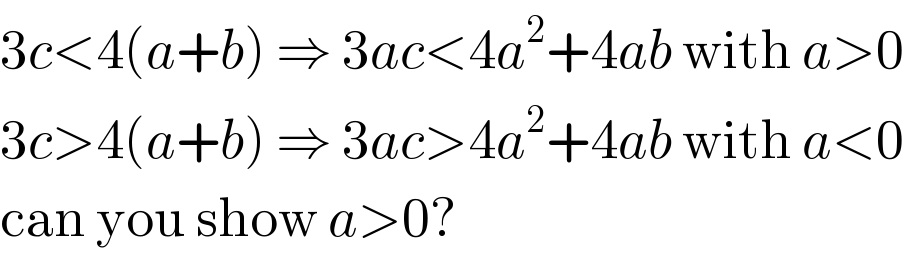
	Answered by saru53424@gmail.com last updated on 24/Mar/18

	$t h a n k s$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum