Question and Answers Forum

All Questions      Topic List

Logarithms Questions

Previous in All Question      Next in All Question      

Previous in Logarithms      Next in Logarithms      

Question Number 3239 by Rasheed Soomro last updated on 08/Dec/15

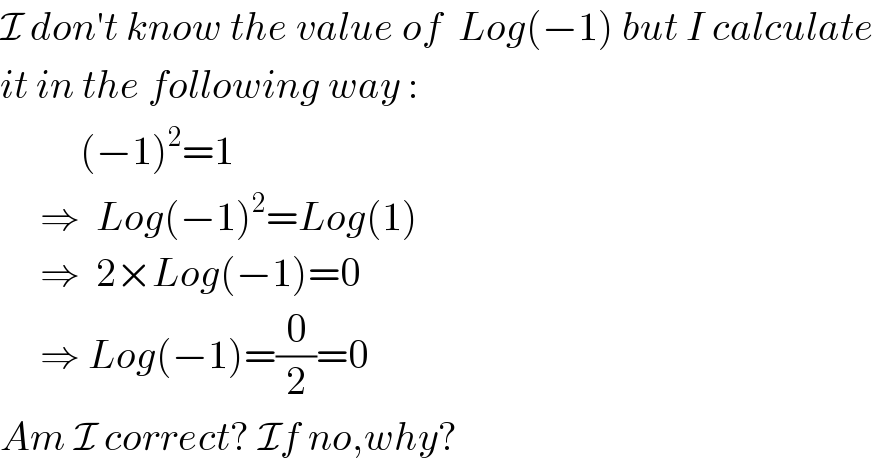
I don′t know the value of Log(−1) but I calculate it in the following way : (−1)^2 =1 ⇒ Log(−1)^2 =Log(1) ⇒ 2×Log(−1)=0 ⇒ Log(−1)=(0/2)=0 Am I correct? If no,why?

$$\mathcal{I}\:{don}'{t}\:{know}\:{the}\:{value}\:{of}\:\:{Log}\left(−\mathrm{1}\right)\:{but}\:{I}\:{calculate} \\ $$$${it}\:{in}\:{the}\:{following}\:{way}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\:\:\:\:\:\Rightarrow\:\:{Log}\left(−\mathrm{1}\right)^{\mathrm{2}} ={Log}\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\Rightarrow\:\:\mathrm{2}×{Log}\left(−\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\Rightarrow\:{Log}\left(−\mathrm{1}\right)=\frac{\mathrm{0}}{\mathrm{2}}=\mathrm{0} \\ $$$${Am}\:\mathcal{I}\:{correct}?\:\mathcal{I}{f}\:{no},{why}? \\ $$

Commented by prakash jain last updated on 08/Dec/15

y=e^x ⇒x=ln y e^(ix) =−1⇒cos x+isin x=−1 x=(2n+1)π ln (−1)=i(2n+1)π

$${y}={e}^{{x}} \Rightarrow{x}=\mathrm{ln}\:{y} \\ $$$${e}^{{ix}} =−\mathrm{1}\Rightarrow\mathrm{cos}\:{x}+{i}\mathrm{sin}\:{x}=−\mathrm{1} \\ $$$${x}=\left(\mathrm{2}{n}+\mathrm{1}\right)\pi \\ $$$$\mathrm{ln}\:\left(−\mathrm{1}\right)={i}\left(\mathrm{2}{n}+\mathrm{1}\right)\pi \\ $$

Commented by prakash jain last updated on 08/Dec/15

a^2 =b^2 ⇏a=b

$${a}^{\mathrm{2}} ={b}^{\mathrm{2}} \nRightarrow{a}={b} \\ $$

Commented by Rasheed Soomro last updated on 08/Dec/15

But we have not extracted square root of both sides .

$$\mathcal{B}{ut}\:{we}\:{have}\:{not}\:{extracted}\:{square}\:{root}\:{of}\:{both}\:{sides}\:. \\ $$

Commented by prakash jain last updated on 08/Dec/15

a=b ln ((√a))^2 =ln b 2ln (√a)=ln b ln (√a)=(1/2)ln b=ln (√b) a=b=1 LHS=(√a)=−1 RHS=(√b)=1

$${a}={b} \\ $$$$\mathrm{ln}\:\left(\sqrt{\mathrm{a}}\right)^{\mathrm{2}} =\mathrm{ln}\:{b} \\ $$$$\mathrm{2ln}\:\sqrt{{a}}=\mathrm{ln}\:{b} \\ $$$$\mathrm{ln}\:\sqrt{{a}}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{b}=\mathrm{ln}\:\sqrt{{b}} \\ $$$${a}={b}=\mathrm{1} \\ $$$$\mathrm{LHS}=\sqrt{{a}}=−\mathrm{1} \\ $$$$\mathrm{RHS}=\sqrt{\mathrm{b}}=\mathrm{1} \\ $$

Commented by Rasheed Soomro last updated on 08/Dec/15

Ok Sir!

$$\mathcal{O}{k}\:\mathcal{S}{ir}! \\ $$

Commented by prakash jain last updated on 09/Dec/15

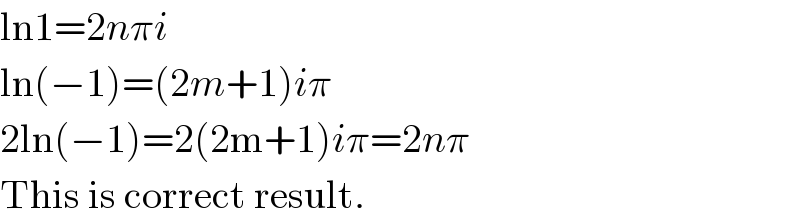
ln1=2nπi ln(−1)=(2m+1)iπ 2ln(−1)=2(2m+1)iπ=2nπ This is correct result.

$$\mathrm{ln1}=\mathrm{2}{n}\pi{i} \\ $$$$\mathrm{ln}\left(−\mathrm{1}\right)=\left(\mathrm{2}{m}+\mathrm{1}\right){i}\pi \\ $$$$\mathrm{2ln}\left(−\mathrm{1}\right)=\mathrm{2}\left(\mathrm{2m}+\mathrm{1}\right){i}\pi=\mathrm{2}{n}\pi \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{result}. \\ $$

Commented by 123456 last updated on 08/Dec/15

e^(2πı) =e^0 but 2πı≠0

$${e}^{\mathrm{2}\pi\imath} ={e}^{\mathrm{0}} \:\mathrm{but}\:\mathrm{2}\pi\imath\neq\mathrm{0} \\ $$

Commented by 123456 last updated on 08/Dec/15

e^x =e^y ⇔x=y work only for (x,y)∈R^2 at complex plane e^z dont is one to one in fact e^(z+2πnı) =e^z n∈Z

$${e}^{{x}} ={e}^{{y}} \Leftrightarrow{x}={y}\:\mathrm{work}\:\mathrm{only}\:\mathrm{for}\:\left({x},{y}\right)\in\mathbb{R}^{\mathrm{2}} \\ $$$$\mathrm{at}\:\mathrm{complex}\:\mathrm{plane}\:{e}^{{z}} \:\mathrm{dont}\:\mathrm{is}\:\mathrm{one}\:\mathrm{to}\:\mathrm{one} \\ $$$$\mathrm{in}\:\mathrm{fact} \\ $$$${e}^{{z}+\mathrm{2}\pi{n}\imath} ={e}^{{z}} \:\:\:\:\:\:{n}\in\mathbb{Z} \\ $$

Commented by Rasheed Soomro last updated on 08/Dec/15

THanK^S S_(S!) !^!

$$\mathbb{T}\boldsymbol{\mathrm{Han}}\mathbb{K}^{\mathbb{S}} \mathbb{S}_{\mathbb{S}!} !^{!} \\ $$

Commented by 123456 last updated on 09/Dec/15

just random comment ln1=2πnı 2ln(−1)=2(πı+mπı)=2π(1+m)ı ln(−1)^2 =2ln(−1) n=1+m lnz=ln∣z∣+ı[arg(z)+2πk]

$$\mathrm{just}\:\mathrm{random}\:\mathrm{comment} \\ $$$$\mathrm{ln1}=\mathrm{2}\pi{n}\imath \\ $$$$\mathrm{2ln}\left(−\mathrm{1}\right)=\mathrm{2}\left(\pi\imath+{m}\pi\imath\right)=\mathrm{2}\pi\left(\mathrm{1}+{m}\right)\imath \\ $$$$\mathrm{ln}\left(−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2ln}\left(−\mathrm{1}\right) \\ $$$${n}=\mathrm{1}+{m} \\ $$$$\mathrm{ln}{z}=\mathrm{ln}\mid{z}\mid+\imath\left[\mathrm{arg}\left({z}\right)+\mathrm{2}\pi{k}\right] \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com