
Question and Answers Forum
Question Number 32480 by prof Abdo imad last updated on 25/Mar/18
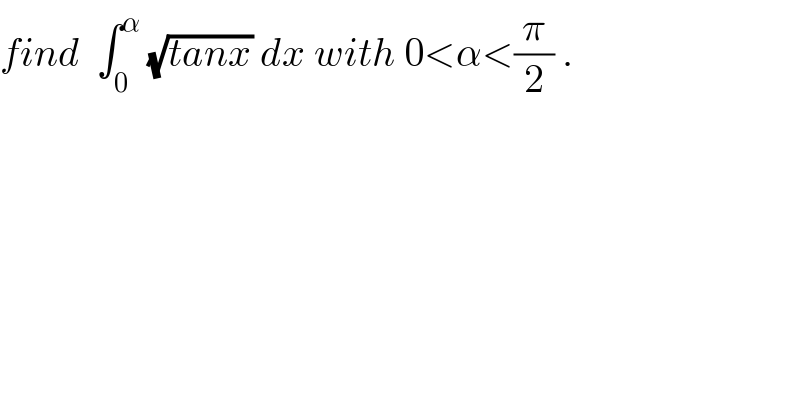
Commented byprof Abdo imad last updated on 14/Apr/18
![let put I = ∫_0 ^α (√(tanx)) dx .changement (√(tanx)) =t give x =arctan(t^2 ) and I = ∫_0 ^(√(tanα)) t .((2tdt)/(1+t^4 )) = ∫_0 ^(√(tanα)) ((2t^2 )/(1+t^4 )) dt = (1/2) ∫_0 ^(√(tanα)) (1/t) ((4t^3 )/(1+t^4 )) dt by parts u =(1/t) and v^′ = ((4t^3 )/(1+t^4 )) ⇒ I = [(1/t) ln(1+t^4 )]_0 ^(√(tanα)) − ∫_0 ^(√(tanα)) ((−1)/t^2 ) ln(1+t^4 ) dt = (1/(√(tanα))) ln( 1 +tan^2 α) + ∫_0 ^(√(tanα)) ((ln(1+t^4 ))/t^2 ) dt if 0< α< (π/4) ⇒ 0<(√(tanα))<1 so let developp ln(1+t^4 ) we have ln(1 +u)^′ =Σ (−1)^n u^n ln(1+u) =Σ _(n≥0) (((−1)^n u^(n+1) )/(n+1)) = Σ_(n=1) ^∞ (−1)^(n−1) (u^n /n) ln(1+x^4 ) = Σ_(n=1) ^∞ (−1)^(n−1) (x^(4n) /n) ⇒ ((ln(1+t^4 ))/t^2 ) = Σ_(n=1) ^∞ (−1)^(n−1) (t^(4n−2) /n) ⇒ ∫_0 ^(√(tanα)) ((ln(1+t^4 ))/t^2 ) dt = Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ∫_0 ^(√(tanα)) t^(4n−2) dt = Σ_(n=1) ^∞ (((−1)^(n−1) )/n) (1/(4n−1)) (tanα)^(2n−1) let put S(x) = Σ_(n=1) ^∞ (((−1)^(n−1) )/n) (1/(4n−1)) x^(2n−1) let find S(x) (1/4) S(x) = Σ_(n=1) ^∞ (((−1)^(n−1) )/((4n−1)(4n))) x^(2n−1) = Σ_(n=1) ^∞ (−1)^(n−1) ( (1/(4n−1)) −(1/(4n))) x^(2n−1) =Σ_(n=1) ^∞ (((−1)^(n−1) )/(4n−1)) x^(2n−1) −(1/4) Σ_(n=1) ^∞ (((−1)^(n−1) )/n) x^(2n−1) ...be continued...](Q33260.png)
| ||
Question and Answers Forum | ||
Question Number 32480 by prof Abdo imad last updated on 25/Mar/18 | ||
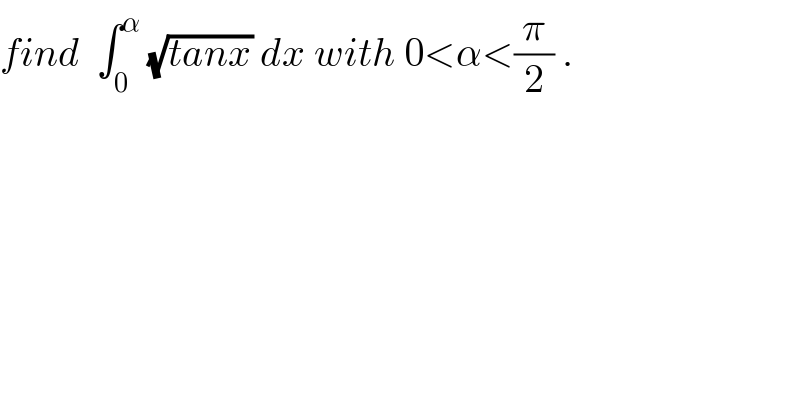 | ||
Commented byprof Abdo imad last updated on 14/Apr/18 | ||
![let put I = ∫_0 ^α (√(tanx)) dx .changement (√(tanx)) =t give x =arctan(t^2 ) and I = ∫_0 ^(√(tanα)) t .((2tdt)/(1+t^4 )) = ∫_0 ^(√(tanα)) ((2t^2 )/(1+t^4 )) dt = (1/2) ∫_0 ^(√(tanα)) (1/t) ((4t^3 )/(1+t^4 )) dt by parts u =(1/t) and v^′ = ((4t^3 )/(1+t^4 )) ⇒ I = [(1/t) ln(1+t^4 )]_0 ^(√(tanα)) − ∫_0 ^(√(tanα)) ((−1)/t^2 ) ln(1+t^4 ) dt = (1/(√(tanα))) ln( 1 +tan^2 α) + ∫_0 ^(√(tanα)) ((ln(1+t^4 ))/t^2 ) dt if 0< α< (π/4) ⇒ 0<(√(tanα))<1 so let developp ln(1+t^4 ) we have ln(1 +u)^′ =Σ (−1)^n u^n ln(1+u) =Σ _(n≥0) (((−1)^n u^(n+1) )/(n+1)) = Σ_(n=1) ^∞ (−1)^(n−1) (u^n /n) ln(1+x^4 ) = Σ_(n=1) ^∞ (−1)^(n−1) (x^(4n) /n) ⇒ ((ln(1+t^4 ))/t^2 ) = Σ_(n=1) ^∞ (−1)^(n−1) (t^(4n−2) /n) ⇒ ∫_0 ^(√(tanα)) ((ln(1+t^4 ))/t^2 ) dt = Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ∫_0 ^(√(tanα)) t^(4n−2) dt = Σ_(n=1) ^∞ (((−1)^(n−1) )/n) (1/(4n−1)) (tanα)^(2n−1) let put S(x) = Σ_(n=1) ^∞ (((−1)^(n−1) )/n) (1/(4n−1)) x^(2n−1) let find S(x) (1/4) S(x) = Σ_(n=1) ^∞ (((−1)^(n−1) )/((4n−1)(4n))) x^(2n−1) = Σ_(n=1) ^∞ (−1)^(n−1) ( (1/(4n−1)) −(1/(4n))) x^(2n−1) =Σ_(n=1) ^∞ (((−1)^(n−1) )/(4n−1)) x^(2n−1) −(1/4) Σ_(n=1) ^∞ (((−1)^(n−1) )/n) x^(2n−1) ...be continued...](Q33260.png) | ||